Как рассадить необщительных посетителей в баре так, чтобы клиентов было как можно больше?

В этот бар ходят необщительные посетители. Вдоль барной стойки расположены 25 мест. Всякий раз, когда входит новый посетитель, он обязательно садится на самое дальнее, насколько это возможно, место от остальных гостей. Ни один не сядет рядом с кем-то другим: если посетитель входит и видит, что «свободных» мест нет, он тут же разворачивается и уходит из бара. Бармену, естественно, хочется, чтобы за стойкой сидело как можно больше клиентов. Если ему разрешено усадить первого посетителя на любое место, куда выгоднее его посадить с точки зрения бармена?

Самый плотный из возможных вариантов — чередование клиентов и пустых мест, при котором оба крайних места заняты. Это позволило бы остальным посетителям сесть на все места с нечетными номерами, в том числе и крайние под номерами 1 и 25, и оставить все четные номера пустыми. В этом случае у стойки могло бы разместиться 13 клиентов.

Однако такое размещение не всегда работает. Предположим, первый клиент уселся на место № 1. Следующий «отшельник» выбирает место под номером № 25, поскольку оно располагается на самом далеком из всех возможных расстояний от № 1 Третьему клиенту придется сесть в середину барной стойки, на место № 13. Два следующих посетителя заполнят пустоты и усядутся соответственно на места № 7 и № 19. Пока все хорошо.

В конце концов, кто–то захочет сесть между клиентами, занимающими места № 1 и № 7. Он выберет № 4, поскольку это позволит ему иметь два пустых сиденья между собой и ближайшими соседями. Но ни один из следующих гостей не сядет рядом с ним. Остальная часть барной стойки заполнится точно так же, и поэтому между двумя посетителями будут пустоты в два места, что делает эту схему минимально эффективной из возможных (при ней у стойки окажутся лишь девять клиентов вместо оптимального числа — 13).

Многие задачи, в том числе и эту, лучше всего решать, двигаясь от конца к началу. Мы знаем, каким должен быть желательный для нас план рассадки, и надо определить, как на него выйти.

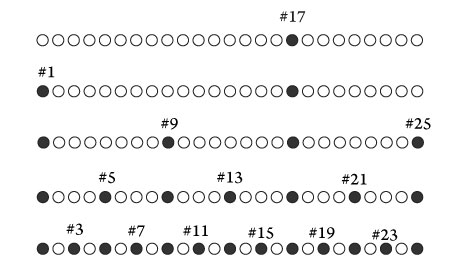
Как показано на диаграмме, для этой схемы характерна большая симметрия, напоминающая рост кристалла. Небольшие части барной стойки заполняются как раз таким образом. Обратите внимание на ту часть стойки, в которой идут первые номера. Нужно, чтобы посетители заняли места № 1 и № 5, так как это позволит другому клиенту усесться на № 3.

Как вам добиться, чтобы пришедший в бар человек сел на место № 5? Ответ: надо, чтобы клиенты уже сидели на местах № 1 и № 9. Тогда пятое место будет посредине между ними, поскольку оно занимает максимальное расстояние и от № 1, и от № 9.

Как добиться, чтобы человек сел на № 9? Для этого предыдущие клиенты должны занять № 1 и № 17. А как сделать так, чтобы посетитель отправился на № 17? Скажем так, барная стойка недостаточно длинная, чтобы посадить клиентов на места № 1 и № 33. Поэтому бармену придется поступить просто — попросить первого посетителя сесть за № 17. Вот ответ.

Давайте отмотаем пленку назад. Первый клиент усаживается на № 17 (верхняя строка в диаграмме). Второй посетитель усаживается от него как можно дальше, на место № 1.

У третьего посетителя два варианта выбора: место № 9 пли № 25. Оба находятся на расстоянии семи пустых мест от любого другого клиента. Если исходить из замкнутого характера посетителей этого бара, третий клиент выберет скорее всего место № 25, поскольку в этом случае у него на расстоянии будет всего один сосед, а не двое, между которыми ему придется сидеть, и поэтому № 9 остается для четвертого клиента.

Следующие три посетителя выберут места между первыми четырьмя и займут соответственно места № 5, № 13 и № 21. На каждом из этих мест до ближайшего соседа их будет разделять три пустых сиденья.

И наконец, следующие шесть посетителей займут шесть оставшихся мест, у которых нет ближайших соседей, а именно: № 3, № 7, № 11, № 15, № 19 и № 23.

Бармен с таким же успехом мог бы попросить первого посетителя сесть на место № 9, и в этом случае диаграмма стала бы зеркальным отображением той, которая представлена выше.
Разбор по книге «Действительно ли Вы достаточно умны, чтобы работать в Google?»