Что такое рекурсия и как с ней работать: разбираемся на примерах

Рекурсия — это мощный инструмент в программировании, который позволяет решать задачи, разбивая их на более простые подзадачи. В статье рассмотрим базовые понятия рекурсии, её принципы, примеры использования, а также типичные проблемы, с которыми можно столкнуться при написании кода.

Рекурсия: что это такое и зачем нужна

Рекурсия — функция, которая вызывает саму себя. Ее базовое применение — разбить большую задачу на несколько мелких, что делает код проще и понятнее, или когда нужно повторить какое-то действие несколько раз. Второй случай похож на русскую матрешку — вы достаете куклу за куклой, пока не дойдете до самой маленькой.

А теперь давайте разберемся на простом примере из математики: представим, что у нас есть функция F, которая выполняет определенное действие. В нашем случае — вычисляет факториал числа (это самый классический пример). Внутри этой функции F в качестве одного из значений используем вызов этой же функции F, но с уменьшенным аргументом. Так функция будет вызывать саму себя до тех пор, пока не достигнет базового случая (о нем расскажем ниже), после чего начнет возвращать результаты.

В виде кода это выглядит так:

			def F(n):
    if n == 1:  
        return 1  
    return n * F(n - 1)
		

Здесь функция F вычисляет факториал числа n, умножая его на факториал n-1, и так до тех пор, пока не дойдёт до 1, после чего начнёт возвращать результаты вверх по цепочке вызовов. Этот пример как раз о том, что нужно выполнить несколько одинаковых действий.

А вот пример из жизни: вы листаете ленту в известной социальной сети, а новые посты обновляются автоматически — это рекурсия в действии.

Принципы работы рекурсии

Рекурсия строится на двух ключевых принципах: базовый случай и рекурсивный вызов. Они позволяют функции вызывать саму себя, пока она не завершится.

Базовый случай

Базовый случай рекурсии — условие, при котором рекурсивный вызов прекращается. Без него функция будет вызывать саму себя бесконечно, а значит, стек переполнится.

Один из самых простых примеров — факториал, о котором мы писали выше. Другой — возведение числа в степень до тех пор, пока значение не станет равно искомому.

Так это выглядит в виде кода:

			def power(base, exponent):
    if exponent == 0:  # базовый случай, любое число в степени 0 равно 1
        return 1
		

То есть, базовый случай — если exponent == 0, то возвращаем 1.

Рекурсивный вызов

Рекурсивный вызов — шаг, на котором функция вызывает саму себя, но с измененными параметрами, чтобы задача стала проще. Один из еще одних классических примеров — задача с числами Фибоначчи.

			def fibonacci(n):
    if n == 0:  # базовый случай
        return 0
    if n == 1:  # базовый случай
        return 1
    return fibonacci(n - 1) + fibonacci(n - 2)  # рекурсивный вызов
		

Числа Фибоначчи — это последовательность, где каждое число равно сумме двух предыдущих: 0, 1, 1, 2, 3, 5, 8, 13, 21, …

Если вызвать fibonacci(5), то увидите следующее:

			fibonacci(5) → fibonacci(4) + fibonacci(3)
fibonacci(4) → fibonacci(3) + fibonacci(2)
fibonacci(3) → fibonacci(2) + fibonacci(1)
fibonacci(2) → fibonacci(1) + fibonacci(0)
fibonacci(1) → 1  (базовый случай)
fibonacci(0) → 0  (базовый случай)

		

После этого функция возвращает результаты обратно вверх по стеку вызовов. Обычно этот метод используется в криптографии и алгосах.

Кстати, на примере чисел Фибоначчи можно разобрать одну из проблем рекурсии — плохая производительность при отсутствии мемоизации.

Мемоизация — техника оптимизации, при которой результаты больших вычислений сохраняются и используются еще раз при повторных вызовах функции. Это особенно полезно, если работаете с рекурсиями, которые могут вычислять одни и те же значения много раз.

Так, функция в задаче с числами Фибоначчи имеет экспоненциальную сложность O(2^n), так как она многократно вычисляет одни и те же значения. Например, чтобы вычислить fibonacci(5), функция вызывает сама себя 15 раз, хотя уникальных вычислений всего 6.

Чтобы улучшить производительность, нужно использовать мемоизацию, чтобы сохранить результаты:

			def fibonacci_memo(n, memo={}):
    if n in memo:
        return memo[n]
    if n <= 1:
        return n
    memo[n] = fibonacci_memo(n - 1, memo) + fibonacci_memo(n - 2, memo)
    return memo[n]
		

Здесь сложность уменьшается до O(n), так как каждое значение вычисляется только один раз.

Стек вызовов и управление памятью

Каждый рекурсивный вызов функции добавляет новый элемент в стек вызовов. Это значит, что вызовы складывается в стеке до тех пор, пока не будет достигнут базовый случай. После этого стек начинает разворачиваться, возвращая результаты на каждом уровне.

Например:

			def countdown(n):
    if n == 0:  # базовый случай, завершение рекурсии
        print("Старт")
        return  
    print(n)  
    countdown(n - 1)  # рекурсивный вызов

countdown(3)
		

Так, когда мы вызываем сountdows(3), в стеке появляются новые вызовы:

call countdown(3) # → печатает 3

call countdown(2) # → печатает 2

call countdown(1) # → печатает 1

call countdown(0) # → печатает "Старт" и выходит

Затем стек начинает разворачиваться:

• countdown(0) завершился → удаляется из стека
• countdown(1) завершился → удаляется из стека
• countdown(2) завершился → удаляется из стека
• countdown(3) завершился → удаляется из стека

Если же в рекурсии нет базового случая, то стек вызовов никогда не освободится, и программа (в нашем случае на Питоне) выдаст ошибку RecursionError.

Вот пример бесконечной рекурсии:

			def infinite_recursion():
    return infinite_recursion()

infinite_recursion()
		

В Питоне есть ограничения до 1000 вызовов, чтобы не перегружать стек, но этот лимит можно увеличить:

			import sys
sys.setrecursionlimit(2000)
		

Рекурсия на реальных задачах

С базовым случаем и рекурсивным вызовом все понятно, поэтому давайте разбираться на более реальных и сложных примерах — с деревьями, графами и массивами.

Обход структуры данных

Рекурсия часто используется для обхода деревьев и графов. Например, бинарного дерева — в нем не более двух дочерних узлов (левый и правый). Вот три основных способа обхода:

1. Прямой обход (Pre-order): Корень → Левый узел → Правый узел.
2. Симметричный обход (In-order): Левый узел → Корень → Правый узел.
3. Обратный обход (Post-order): Левый узел → Правый узел → Корень.

Запишем в виде кода:

			class TreeNode:
    def __init__(self, value):
        self.value = value
        self.left = None
        self.right = None

# прямой обход
def pre_order_traversal(node):
    if node is None:  # базовый случай
        return
    print(node.value)  # обработка текущего узла
    pre_order_traversal(node.left)  # обход левого поддерева
    pre_order_traversal(node.right)  # обход правого поддерева

# Симметричный обход
def in_order_traversal(node):
    if node is None:  # базовый случай
        return
    in_order_traversal(node.left)  # обход левого поддерева
    print(node.value)  # текущего узла
    in_order_traversal(node.right)  # обход правого поддерева

# Обратный обход
def post_order_traversal(node):
    if node is None:  # базовый случай
        return
    post_order_traversal(node.left)  # обход левого поддерева
    post_order_traversal(node.right)  # обход правого поддерева
    print(node.value)  # обработка текущего узла
		

Дерево будет выглядеть так:

1

/ \

2 3

/ \

4 5

• Прямой обход: 1 → 2 → 4 → 5 → 3.
• Симметричный обход: 4 → 2 → 5 → 1 → 3.
• Обратный обход: 4 → 5 → 2 → 3 → 1.

Обходить можно и графы, особенно в глубине (DFS). Вот пример:

			def dfs(graph, node, visited=None):
    if visited is None:
        visited = set()  # отслеживание вершин
    if node not in visited:
        print(node)  # обработка текущей вершины
        visited.add(node)  # помечаем вершину посещенной
        for neighbor in graph[node]:  # рекурсивный обход соседних вершин
            dfs(graph, neighbor, visited)
		

Сам граф:

			graph = {
    'A': ['B', 'C'],
    'B': ['D', 'E'],
    'C': ['F'],
    'D': [],
    'E': ['F'],
    'F': []
}
		

Результат обхода: A → B → D → E → F → C.

Разбиение

Разбить можно массив или строку. Давайте разбираться на примере строки. Так, рекурсия может разбить строку на слова или разделить ее по конкретным символам. Выглядит это так:

			s = "Hello World How Are You"
def split_string(s, space=' '):
    if space not in s:  # базовый случай
        return [s]
    index = s.index(space)  # ищем индекс разделителя
    return [s[:index]] + split_string(s[index + 1:], space)  # рекурсивное разбиение
print(split_string(s))  

> ['Hello', 'World', 'How', 'Are', 'You']


		

Что такое хвостовая рекурсия

Хвостовая (оконечная) рекурсия — частный случай рекурсии. Главное отличие от обычной в том, что единственный рекурсивный вызов находится в конце перед выходом функции. В традиционной же рекурсии после рекурсивного вызова могут быть дополнительные вычисления.

Вот пример:

			def factorial_tail_recursive(n, accumulator=1):
    if n == 1:  # базовый случай
        return accumulator
    return factorial_tail_recursive(n - 1, n * accumulator)  # хвостовой вызов
		

Кстати, с помощью хвостовой рекурсии тоже можно решать задачи с числами Фибоначчи:

			def fibonacci__recursive(n, a=0, b=1):
    if n == 0:  # базовый случай
        return a
    if n == 1:  # базовый случай
        return b
    return fibonacci__recursive(n - 1, b, a + b)  # хвостовой вызов
		

Некоторые языки программирования (например, Haskell и Scala) поддерживают оптимизацию хвостовой рекурсии. Это означает, что компилятор или интерпретатор преобразует хвостовую рекурсию в итерацию — это помогает избежать переполнение стека.

Давайте посмотрим, как это работает в Scala. Вот обычная рекурсия, чтобы понять принцип:

			def sumList(list: List[Int]): Int = {
  if (list.isEmpty) 0
  else list.head + sumList(list.tail)  // обычный рекурсивный вызов
}
		

А вот рекурсия с оптимизацией:

			def sumList(list: List[Int]): Int = {
  @annotation.tailrec  // Аннотация для проверки хвостовой рекурсии
  def loop(acc: Int, list: List[Int]): Int = {
    if (list.isEmpty) acc
    else loop(acc + list.head, list.tail)  // хвостовой вызов
  }
  loop(0, list)
}
		

К сожалению, наш любимый Питон такую функцию не поддерживает, но всегда можно преобразовать «хвостика» в итерацию вручную:

			def factorial_iterative(n):
    accumulator = 1
    for i in range(1, n + 1):
        accumulator *= i
    return accumulator
		

Это пример итеративного решения факториала.

Рекурсия vs. итерация

Основные различия между рекурсией и итерацией заключаются в следующем:

• В рекурсии функция вызывает саму себя, а в итерации используются циклы.
• Интеграция требует меньше памяти, потому что нет стека вызовов.
• Рекурсия медленнее без оптимизации.
• С рекурсией легко переполнить хранилище при большой глубине.
• Рекурсия обычно более читаемая и лаконичная, но подходит для меньшего количества задач.

Итерацию лучше использовать в следующих случаях:

• Задачи, где нужна производительность. Как, например, с итеративным вычислением чисел Фибоначчи.
• Обработка больших данных, например, поиск или сортировка. Вот пример пузырьковой сортировки:

			def bubble_sort(arr):
    n = len(arr)
    for i in range(n):
        for j in range(0, n - i - 1):
            if arr[j] > arr[j + 1]:
                arr[j], arr[j + 1] = arr[j + 1], arr[j]
		

• Задачи с большой глубиной рекурсии, чтобы стек не переполнялся. Вот как итеративно обойти дерево:

			def iterative_tree_traversal(root):
    stack = [root]
    while stack:
        node = stack.pop()
        print(node.value)
        if node.right:
            stack.append(node.right)
        if node.left:
            stack.append(node.left)

		

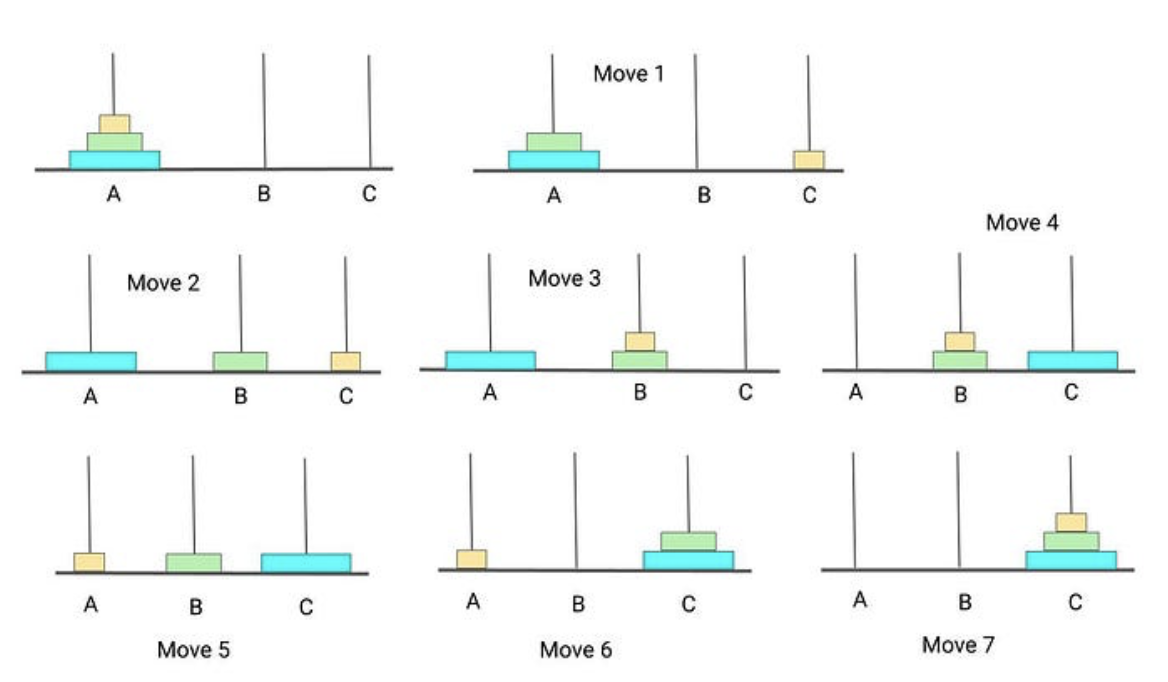
Еще один пример: задача «Ханойские башни»

«Ханойские башни» — классная головоломка, которую часто решают с помощью рекурсии. Считайте, что это еще одна классика.

Есть три стержня: A, B и C. На стержень A нанизано несколько дисков разного размера, причем диски упорядочены по размеру в виде пирамидки — вниз от маленького к большому. Суть в том, чтобы переместить все диски со стержня А на С, при этом: за один раз можно перемещать только один диск, нельзя класть больший диск на меньший, можно использовать стержень B как вспомогательный.

Рекурсивное решение задачи «Ханойские башни» основано на следующей идее:

1. Переместить (n−1) дисков с A на B, используя C как промежуточный.
2. Переместить оставшийся самый большой диск с A на C.
3. Переместить (n−1) дисков с B) на C, теперь используя A как промежуточный.

Следовательно, если количество дисков n=1, просто переместите его с А на С (базовый случай). В остальных случаях при n–1 повторить то, что указано выше.

А теперь решение с помощью кода:

			def hanoi(n, start, finish, storage):
   if n == 1:  # базовый случай
       print(f"Переместить диск 1 с {start} на {finish}")
       return
   # Рекурсивный случай
   hanoi(n - 1, start, storage, finish)  # переместить n-1 дисков на вспомогательный стержень
   print(f"Переместить диск {n} с {start} на {finish}")  # Переместить оставшийся диск на целевой стержень
   hanoi(n - 1, storage, finish, start)  # Переместить n-1 дисков с вспомогательного на целевой стержень


# Количество дисков
n = 5
# Вызов функции для решения задачи
hanoi(n, 'A', 'C', 'B')

		

Вывод:

			Переместить диск 1 с A на C
Переместить диск 2 с A на B
Переместить диск 1 с C на B
Переместить диск 3 с A на C
Переместить диск 1 с B на A
Переместить диск 2 с B на C
Переместить диск 1 с A на C
Переместить диск 4 с A на B
...
Переместить диск 3 с A на C
Переместить диск 1 с B на A
Переместить диск 2 с B на C
Переместить диск 1 с A на C

		

Поздравляем, вы великолепны. А если хотите еще потренироваться в рекурсии, то можно написать код для поиска пути в лабиринте (кстати, это чем-то напоминает онлайн-карты и навигаторы) или обратного вывода строки.