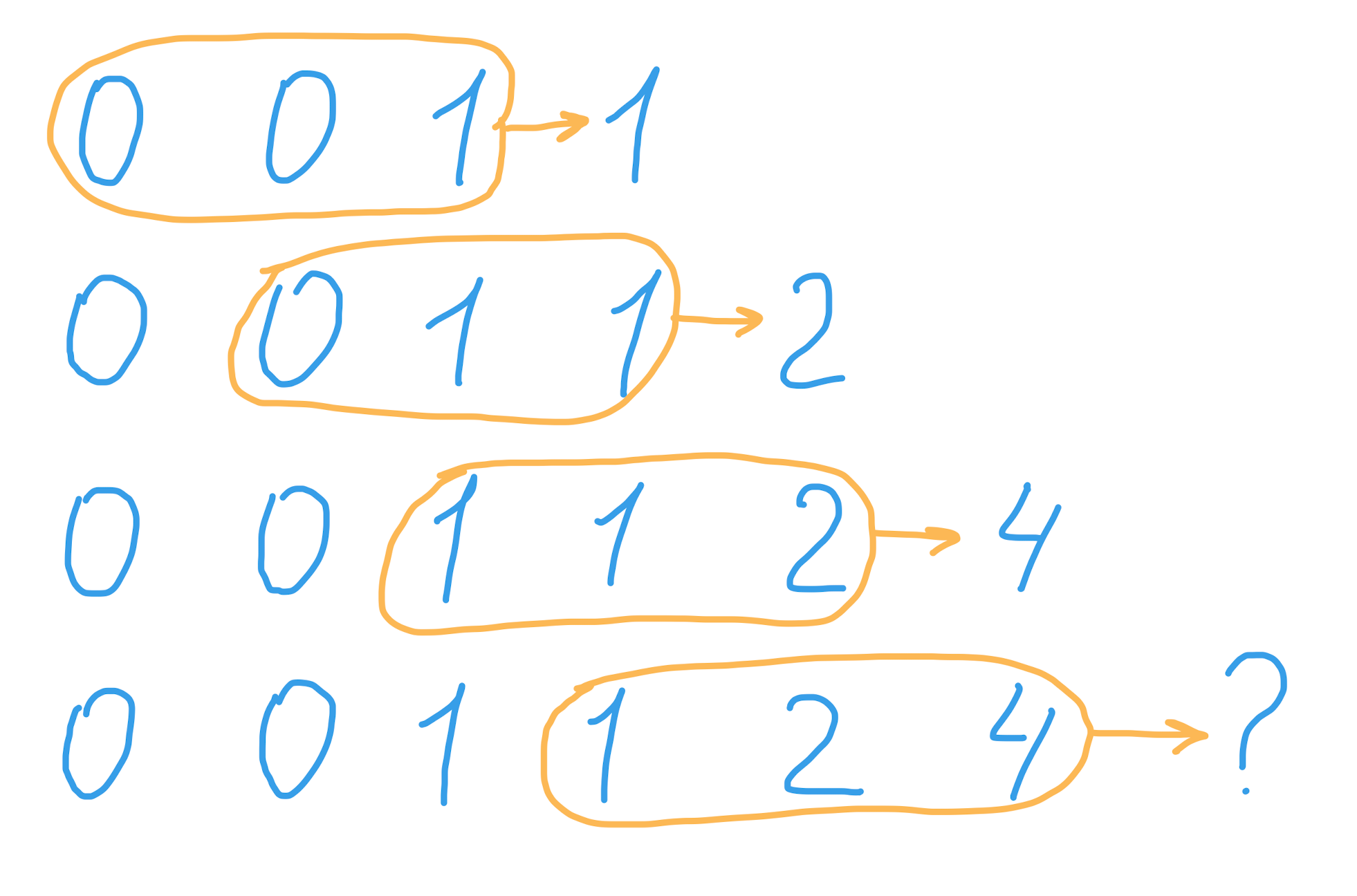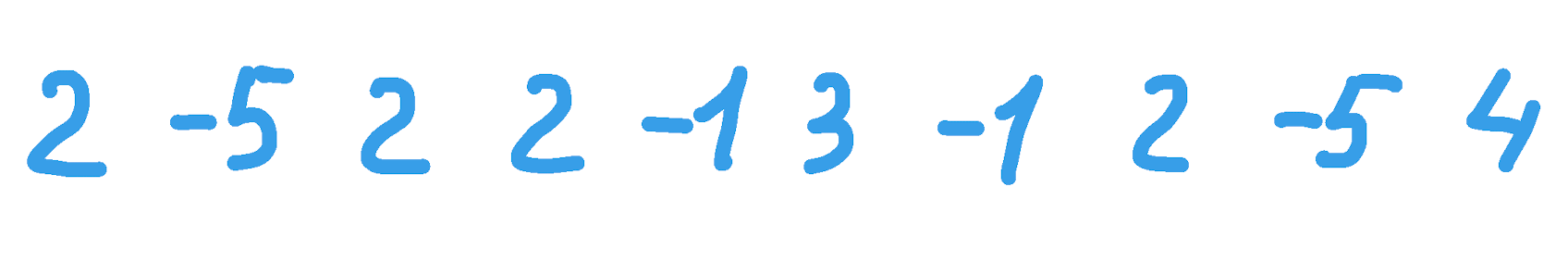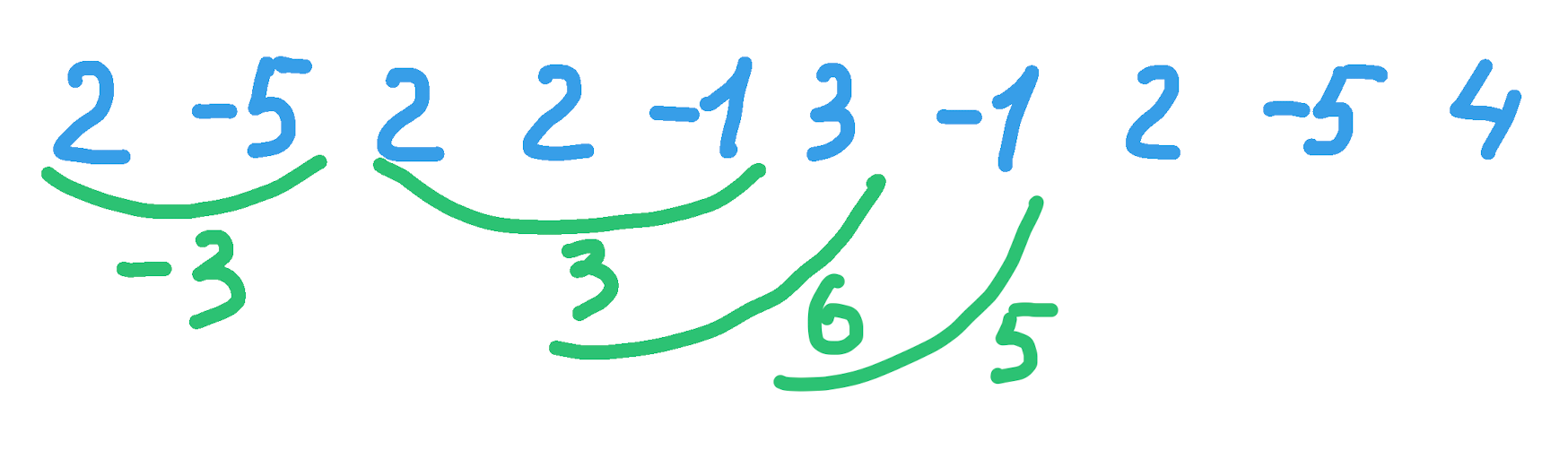Идеи динамического программирования: одномерные задачи, часть 1

Динамическое программирование — способ решения задач путём разбиения их на подзадачи, которые, в свою очередь, используются для нахождения ответа исходной задачи. В этой статье мы разберём несколько классических задач динамического программирования, которые требуют для своего решения одномерный массив, либо, в некоторых случаях, можно даже обойтись без него.

Если вы не знакомы с динамическим программированием, посмотрите эту статью для начинающих.

Числа трибоначчи

Числа трибоначчи — это числовой ряд, начинающийся с трёх чисел 0, 0, 1, где каждое последующее число вычисляется как сумма трёх чисел перед ним:

Рассмотрим следующую задачу: дан массив чисел с порядковыми номерами чисел трибоначчи, например: [73, 10, 4, 15, 20, 7], числа в массиве не превышают 100, требуется вернуть массив, содержащий числа трибоначчи под указанными номерами: [73-е число трибоначчи, 10-е число трибоначчи, и так далее].

Если вы какое-то время работаете с языками программирования, то наверняка решали задачи нахождения факториала или степени числа через рекурсию. Попробуем применить такую же идею здесь:

			const tribonacciNumber = (n) => {
  // обрабатываем граничные условия, их три,
  // т.к. рекурсия будет идти на 3 числа внутрь
  if (n === 1 || n === 2) return 0;
  if (n === 3) return 1;

  return tribonacciNumber(n - 1) +
    tribonacciNumber(n - 2) +
    tribonacciNumber(n - 3);
}
		

Запускаем функцию с вычислением времени:

			console.time();
console.log(tribonacciNumber(36));
console.timeEnd(); // 6337 ms

console.time();
console.log(tribonacciNumber(37));
console.timeEnd(); // 11361 ms

console.time();
console.log(tribonacciNumber(40));
console.timeEnd(); // 71015 ms

console.time();
console.log(tribonacciNumber(41));
console.timeEnd(); // 135573 ms
		

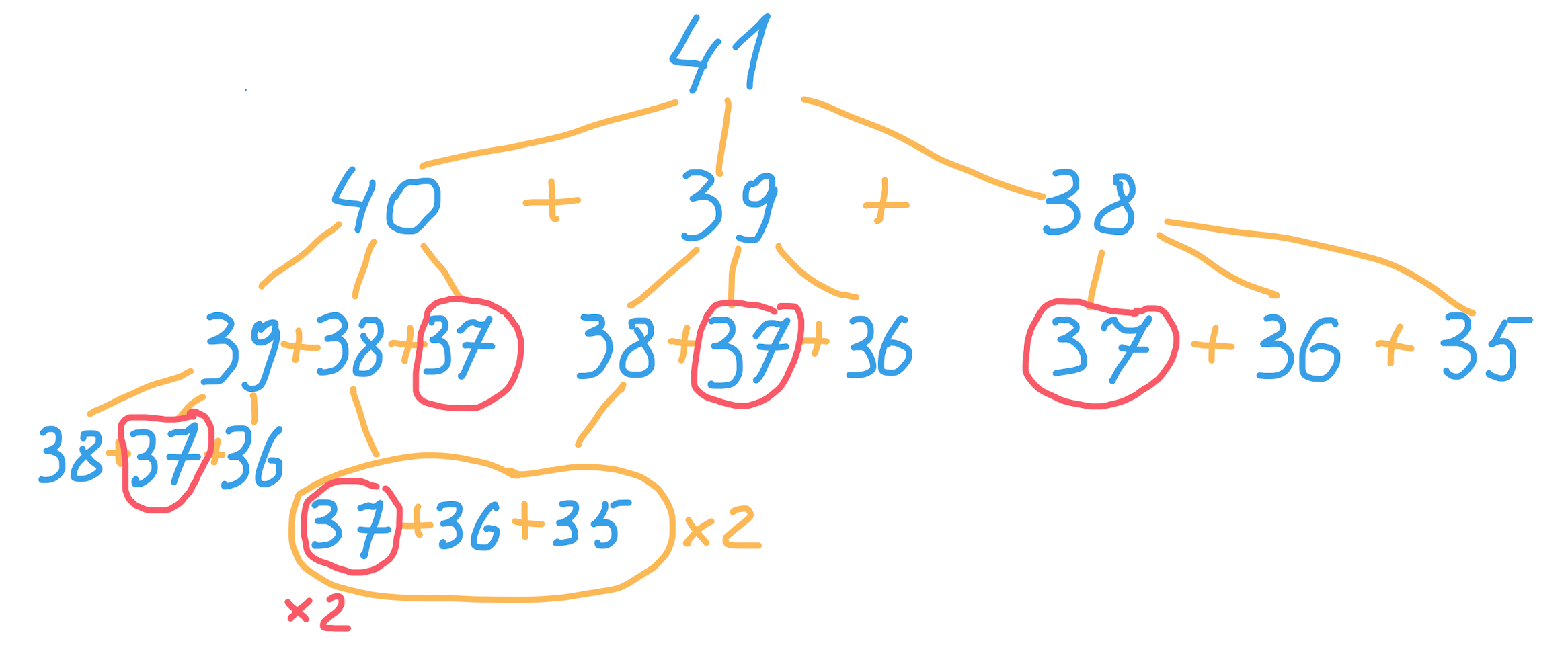
41-е число вычисляется 135 секунд. Кажется, что быстрее вручную посчитать числа, подставить в массив все 100 значений (ограничение задачи) и просто вернуть число на нужной позиции. В чём же проблема, как так получилось, что простой алгоритм работает так долго? Можно заметить, что следующее число вычисляется в 2 раза дольше, чем предыдущее. Давайте посмотрим на рекурсивное дерево вызовов:

Можно заметить, что при вычислении через рекурсию многие числа будут считаться по несколько раз, например, число 37 будет посчитано 6 раз. В замерах времени выше мы видели, что вычисление этого занимает 11 секунд, т.е. займёт половину времени от вычислений числа 41 — 66 секунд из 135.

Напрашивается решение проблемы — запоминать вычисленные значения и при необходимости просто их использовать. Давайте посмотрим, что получается в таком случае:

			// хранит вычисленные числа трибонначи,
// в виде "число трибонначи": "значение числа"
const tribonacciNumbersCache = {};

const tribonacciNumber = (n) => {
  if (n === 1 || n === 2) return 0;
  if (n === 3) return 1;

	// проверяем, было ли вычислено значение числа n
	// если да, то просто возвращаем это значение
	if (n in tribonacciNumbersCache) {
	  return tribonacciNumbersCache[n];
  }
  
	// вычисляем значения
	const nTribonacciNumber = tribonacciNumber(n - 1) +
    tribonacciNumber(n - 2) +
    tribonacciNumber(n - 3);
    
	// сохраняем вычисленное значение, для переиспользования
	tribonacciNumbersCache[n] = nTribonacciNumber;
  
	return nTribonacciNumber;
}
		

Пробуем выполнить новую функция с теми же входными данными:

			console.time();
console.log(tribonacciNumber(36));
console.timeEnd(); // 0.26 ms

console.time();
console.log(tribonacciNumber(37));
console.timeEnd(); // 0.11 ms

console.time();
console.log(tribonacciNumber(40));
console.timeEnd(); // 0.10 ms

console.time();
console.log(tribonacciNumber(41));
console.timeEnd(); // 0.09 ms
		

Во-первых, мы видим, что выполнение теперь занимает доли миллисекунд. Во-вторых, замечаем понижение времени при каждом новом вызове. Это связано с оптимизациями компилятора JavaScript после определенного количества вызова кода. После пары вызовов время уменьшается на 0.1 миллисекунды (для моего компьютера), следовательно, 100 вычислений, которые нам требуются для исходной задачи, пройдут за 0.01 секунду.

Мы уже применили идеи динамического программирования — сохранили результат вычисления подзадачи для получения результата следующей задачи. Осталось вызвать это в цикле для исходного массива и получить ответ. Но что делать, если в вычисления закрадётся ошибка? Код с рекурсией отлаживать довольно сложно.

Давайте немного упростим решение за счёт идеи предварительного вычисления всех возможных вариантов. Это займёт очень мало времени, т.к. по условию задачи максимальное число — 100, и за счет идеи отказа от рекурсии. Будем считать так, как бы мы считали эти числа на листике, руками:

			const tribonacciNumbersCache = [0, 0, 1];

// i < 100, не включая 100, т.к. 100-е число будет находиться в 99 позиции
for (let i = 3; i < 100; i++) {
  // используем предыдущие 3 значение из массива, никакой рекурсии
  tribonacciNumbersCache.push(tribonacciNumbersCache[i - 1] +
    tribonacciNumbersCache[i - 2] +
    tribonacciNumbersCache[i - 3])
}
		

Поскольку идем, увеличивая число i, и у нас изначально добавлено в массив tribonacciNumbersCache три значения, то получение элементов i - 1, i - 2 и i - 3 отработает без ошибок.

В 0 позиций массива tribonacciNumbersCache — первое число трибонначи, главное не забыть вычитать единицу при получении значения.

Напишем решение исходной задачи — по массиву номеров получить массив с числами трибонначи:

			const tribonacciNumbersCache = [0, 0, 1];

for (let i = 3; i < 100; i++) {
  tribonacciNumbersCache.push(tribonacciNumbersCache[i - 1] +
    tribonacciNumbersCache[i - 2] +
    tribonacciNumbersCache[i - 3])
}

const tribonacciNumbers = [73, 10, 4, 15, 20, 7];
// массив для сохранения самих чисел трибонначи
const tribonacciNumbersValue = [];

for (const number of tribonacciNumbers) {
  // просто получаем значения из кеша, не делая никаких вычислений
  tribonacciNumbersValue.push(tribonacciNumbersCache[number - 1])
}

console.log(tribonacciNumbersValue);
		

В консоль будет выведено [2073693258389777400, 44, 1, 927, 19513, 7]. Задача решена.

Задачи на LeetCode и CodeWars для тренировки вычислений чисел фибонначи, трибонначи.

Основные идеи

Мы использовали несколько подходов, типичных для динамического программирования:

1. Определили, как из известных данных маленьких подзадач будет вычисляться следующая подзадача, т.е. с числами трибонначи из трёх значений будет вычисляться следующее значение. Это соотношение называется рекурсивным.
2. Нашли исходные данные, чтобы можно было запустить наше вычисление.
3. Определили, откуда брать ответ — вычитали единицу при обращении к элементу массива с посчитанными значениями.

Кузнечик и кувшинки

Рассмотрим следующую задачу: есть определённое количество кувшинок, расположенных в ряд, кузнечик стоит на первой из них. Он может прыгнуть на следующую кувшинку, либо перепрыгнуть через одну. Сколько существует разных способов (путей) добраться до последней кувшинки?

Рассмотрим вариант с 4-мя кувшинками. Можем перебрать варианты и посчитать, что до последней кувшинки можно добраться 3-мя разными способами:

Грустный кузнечик прыгает по кувшинкам

Рассмотрим сколько способов существует, чтобы добраться до каждой из кувшинок. До второй — 1 способ, до третьей — 2 способа: прыгнуть сразу на неё или прыгнуть с первой кувшинки. До четвёртой уже выяснили перебором, что существует 3 способа.
Можем заметить, что на четвёртую кувшинку мы можем прыгнуть только со второй или с третьей и что количество путей до неё равно количеству путей до второй кувшинки + количество путей до третьей кувшинки. Немного порассуждаем, почему так получается.

С третьей кувшинки на четвёртую есть только один путь — прыгнуть на неё, но при этом до третьей кувшинки было 2 разных пути. Соответственно, если мы двигаемся через третью кувшинку на четвёртую, то так и остается 2 разных пути это сделать. Аналогичные рассуждения можно провести для перемещения со второй на четвёртую кувшинку. Эти два случая будут разными путями, т.к. перед попаданием на четвёртой мы были на разных кувшинках, следовательно, количество путей надо просто сложить.

Аналогичные рассуждения можно провести для дальнейших перемещений, т.е. просто складываем количество путей до предыдущих двух кувшинок.

Понятно, как переходить от одной подзадачи к другой, осталось найти начальные условия. Возьмём за начальные условия количество вариантов попасть на вторую и третью кувшинки, т.е. 1 и 2.

Для нахождения начальных условий можно использовать более математический подход: ввести отрицательные кувшинки, количество путей до них будет 0, и использовать текущую позицию как последнее значение начальных условий. При таком подходе начальные условия будут 0 и 1. В текущей задаче будем использовать первый подход, но для более сложных задач имеет смысл использовать второй.

Получается следующая функция:

			function getNumberOfWaysJumpingWaterLily(n) {
    // количество путей до 1-й и 2-й кувшинки
    const jumpWays = [1, 2];
    
    // если n будет 1 или 2, то тело цикла не выполнится ни разу
    for (let i = 2; i < n; i++) {
        // количество путей до i кувшинки складывается из 2-х путей,
        // до предыдущих кувшинок
        jumpWays.push(jumpWays[i-1] + jumpWays[i-2]);
    }
    
    // в 0 позиции - количество путей до 1-й кувшинки
    // в n - 1 позиции - количество путей до n-й кувшинки
    return jumpWays[n-1];
}

console.log(getNumberOfWaysJumpingWaterLily(10));
		

Задача решена, но можем заметить, что все значения, кроме двух последних, не используются, и упростить решение:

			function getNumberOfWaysJumpingWaterLily(n) {
    let way1 = 1;
    let way2 = 2;
    
    if (n == 1) return way1;
    if (n == 2) return way2;
    
    for (let i = 2; i < n; i++) {
        //за счёт деструктуризации массива смещаем значения
        [way1, way2] = [way2, way1 + way2];
    }
    
    return way2;
};

console.log(getNumberOfWaysJumpingWaterLily(10));
		

В цикле происходит смещение количества путей до i + 1 кувшинки. В начале way1 указывает на количество путей до первой кувшинки, way2 — до второй. После первого выполнения тела цикла way1 указывает на количество путей до второй кувшинки, way2 до третьей, и так далее. В конце выполнения цикла в way2 получится количество путей до n кувшинки.

Задача для практики на LeetCode

Максимальный(по сумме элементов) подмассив

Условие задачи: дан массив чисел, требуется найти непрерывную последовательность чисел с максимальной суммой.

Например, получен такой массив:

Массив для нахождения максимального подмассива

Рассмотрим идею решения. Начнём суммировать значения в этом массиве слева направо. Просуммировав два первых элемента: 2 — 5 = −3, получим отрицательное число. Если добавить это число к следующему, то оно уменьшит его, независимо от того положительное оно или отрицательное. Просуммировав следующие 3 элемента 2 + 2 — 1 = 3, получим положительное значение, которое при добавлении к следующему увеличит сумму с ним в любом случае.

Т.е. мы идём слева направо, суммируя элементы, если сумма становится отрицательной, то игнорируем подсумму, если положительной, то прибавляем дальше:

Суммы, используемые для нахождения максимального подмассива

В процессе этих вычислений при каждом прибавлении сравниваем число с переменной, в которой хранится максимальное подсумма.
Рассмотрим решение в коде:

			const maxSubArraySum = (nums) => {
  // массив, для хранения подсумм, сразу с одним элементом,
  // т.к. в цикле обращаемся к i - 1 элементу
  const arrayOfSums = [nums[0]];
  
  // переменная, для хранения максимальных значений
  let maxSum = nums[0];

  for (let i = 1; i < nums.length; i++) {
    // если подсумма, закончившаяся в предыдущем элементе положительная
    // то используем её с текущим числом
    if (arrayOfSums[i - 1] > 0) {
      // добавляем максимальную подсумму, с текущим числом
      arrayOfSums.push(arrayOfSums[i - 1] + nums[i]);
    } else {
      // если предыдущая подсумма отрицательна, то начинаем подсчет заново
      arrayOfSums.push(nums[i]);
    }

    // на текущем шаге учитываем подсумму, заканчивающуюся в i
    // предыдущие подсуммы были учтены на предыдущих шагах
    if (arrayOfSums[i] > maxSum) {
        maxSum = arrayOfSums[i]
    }
  }

  return maxSum;
};

const sourceArray = [2, -5, 2, 2, -1, 3, -1, 2, -5, 4];
console.log(maxSubArraySum(sourceArray));
		

Рассмотрим массив arrayOfSums, на каждом шаге итерации:

			// исходный массив
// [2, -5, 2, 2, -1, 3, -1, 2, -5, 4]
   [2, -3]
   [2, -3, 2]
   [2, -3, 2, 4]
   [2, -3, 2, 4, 3]
   [2, -3, 2, 4, 3, 6]
   [2, -3, 2, 4, 3, 6, 5]
   [2, -3, 2, 4, 3, 6, 5, 7]
   [2, -3, 2, 4, 3, 6, 5, 7, 2]
   [2, -3, 2, 4, 3, 6, 5, 7, 2, 6]
		

Видим, что максимальное значение 7. Это и будет ответ в текущей задаче.

В решении мы находим только максимальную сумму подмассива, но не находим саму часть массива. По рассмотренному массиву arrayOfSums и логике решения задачи довольно очевидно, как найти требуемый подмассив: находим 7 в массиве arrayOfSums, это будет конец подмассива. Берём слева все положительные числа, самое левое из списка положительных чисел — начало подмассива.

В текущем случае это сумма от второго до седьмого элемента (при отсчёте массива от 0). Подмассив arrayOfSums [2, 4, 3, 6, 5, 7], подмассив исходного массива nums [2, 2, -1, 3, -1, 2].

Реализуем эту идею в коде:

			const maxSubArray = (nums) => {
  const arrayOfSums = [nums[0]];
  let maxSum = nums[0];
  let maxPosition = 0;

  for (let i = 1; i < nums.length; i++) {
    if (arrayOfSums[i - 1] > 0) {
      arrayOfSums.push(arrayOfSums[i - 1] + nums[i]);
    } else {
      arrayOfSums.push(nums[i]);
    }

    if (arrayOfSums[i] > maxSum) {
      maxSum = arrayOfSums[i];
      maxPosition = i;
    }
  }

  // если максимальная сумма - отрицательная
  // значит все элементы в массиве отрицательные
  // на каждом шаге сумма вычислялась заново, и arrayOfSums равен nums
  // возвращаем максимальное из отрицательных чисел, оно будет в maxPosition
  if (maxSum < 0) {
    return nums[maxPosition];
  }

  let endOfMaxSubarray = maxPosition;
  // инициализируем startOfMaxSubarray вне for
  // т.к. переменная понадобится после выполнения цикла
  let startOfMaxSubarray = endOfMaxSubarray;
  
  for (
    ;
    // надо учесть, что можем дойти до начала массива
    startOfMaxSubarray >= 0 && arrayOfSums[startOfMaxSubarray] >= 0;
    startOfMaxSubarray--
  ) {}
  
  // i + 1, т.к. цикл завершится на отрицательном элементе
  // который не нужно суммировать, 
  // либо вне границ массива (в -1 позиции)
  // endOfMaxSubarray + 1, т.к. последний элемент не включается в slice
  return nums.slice(startOfMaxSubarray + 1, endOfMaxSubarray + 1);
};

const sourceArray = [2, -5, 2, 2, -1, 3, -1, 2, -5, 4];

// будет выведено [2, 2, -1, 3, -1, 2]
console.log(maxSubArray(sourceArray));
		

Задача для практики на LeetCode

Заключение

Мы рассмотрели несколько простых задач динамического программирования, желаю успехов в освоении этого непростого, но очень интересного подхода к решению задач.