Книга «Байесовская статистика: Star Wars, LEGO, резиновые уточки и многое другое»

Привет! От издательства «Питер» вышла новая интересная книга — «Байесовская статистика», при покупке с сайта издательства — электронная книга в подарок. Так же есть промокод на скидку в 25%.

Нужно решить конкретную задачу, а перед вами куча непонятных данных, в которой черт ногу сломит? «Байесовская статистика» расскажет, как принимать правильные решения, задействуя свою интуицию и простую математику.

Пора забыть про заумные и занудные университетские лекции! Эта книга даст вам полное понимание байесовской статистики буквально «на пальцах» — с помощью простых объяснений и ярких примеров.

Чтобы узнать, как применить байесовские подходы к реальной жизни, вы отправитесь на охоту за НЛО, поиграете в «Лего», рассчитаете вероятность выживания Хана Соло при полете через поле астероидов, а также узнаете, как оценить вероятность того, что вы не заболели (ковидом?!), несмотря на то, что нагуглили все симптомы родильной горячки.

Прикладные задачи и упражнения помогут закрепить материал и заложить фундамент для работы с широким спектром задач: от невероятных текущих событий до ежедневных сюрпризов делового мира.

Вашему внимаю предлагаю отрывок из главы.

Оценка параметров с априорными вероятностями

В этой главе вы увидите, как можно использовать наши предыдущие вероятности в сочетании с данными наблюдений, чтобы получить более точную оценку, которая сочетает существующие знания с собранными данными.

Прогнозирование коэффициентов конверсии рассылки

Чтобы понять, как изменяется бета-распределение при получении информации, посмотрим на другой коэффициент конверсии. В этом примере мы попытаемся выяснить, с какой скоростью подписчики нажимают на ссылку после того, как они открыли ваше письмо. Большинство компаний, предоставляющих услуги по управлению рассылкой, в реальном времени сообщают вам, сколько людей открыли сообщение и нажали на ссылку.

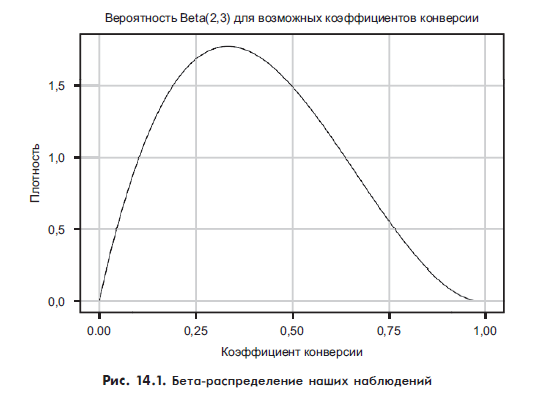
Наши данные пока говорят, что из первых пяти человек, открывших письмо, двое нажимают на ссылку. На рис. 14.1 показано бета-распределение этих данных.

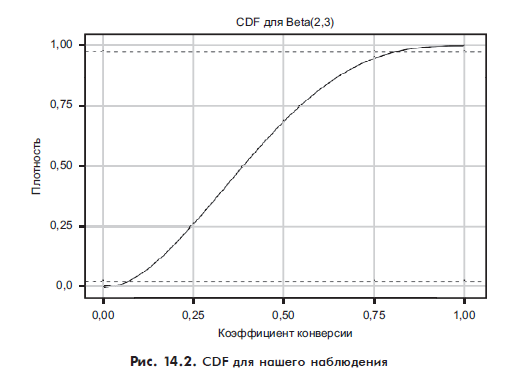
Рисунок 14.1 показывает распределение Beta(2,3). Мы использовали эти цифры, потому что два человека перешли по ссылке, а трое — нет. В отличие от предыдущей главы, где у нас был довольно узкий скачок возможных значений, здесь мы имеем огромный диапазон возможных значений для истинного коэффициента конверсии, потому что у нас очень мало информации для работы. Рисунок 14.2 показывает CDF для этих данных, чтобы помочь нам легче рассуждать об этих вероятностях.

95%-ный доверительный интервал (то есть 95%-ная вероятность того, что истинный коэффициент конверсии находится где-то в этом диапазоне) отмечен, чтобы его было легче увидеть. На данный момент наши данные говорят, что истинный коэффициент конверсии может располагаться где угодно между 0,05 и 0,8! Это отражение того, как мало информации мы на самом деле получили. Учитывая, что у нас было две конверсии, мы знаем, что истинная ставка не может быть равна 0, и, поскольку у нас было три не конверсии, мы также знаем, что она не может быть равна 1. Почти все остальное — справедливо.

Использование широкого контекста с априорными вероятностями

Подождите секунду — вы можете ничего не знать о рассылках, но 80%-ный рейтинг переходов по ссылке — это маловероятно. Я подписываюсь на множество рассылок, но определенно не перехожу к контенту в 80% случаев, когда открываю письмо. Принимать эти 80% за чистую монету кажется наивным, когда я рассматриваю собственное поведение.

Оказывается, ваш провайдер тоже считает это подозрительным. Давайте посмотрим на более широкий контекст. По данным вашего провайдера, для блогов, относящихся к той же категории, что и ваш, только 2,4% людей, открывающих письма, переходят к контенту.

Из главы 9 вы узнали, как можно использовать полученную информацию, чтобы изменить убеждение в том, что Хан Соло может успешно перемещаться по астероидной области. Наши данные говорят одно, но исходная информация утверждает другое.

Как вы уже знаете, в байесовских терминах данные, которые мы наблюдали, являются нашей правдоподобностью, а информация внешнего контекста — в данном случае из личного опыта и от провайдера — априорной вероятностью. Наша задача сейчас состоит в том, чтобы выяснить, как моделировать априорные вероятности. К счастью, в отличие от случая с Ханом Соло у нас действительно имеются данные, чтобы упростить задачу.

Коэффициент конверсии от провайдера, равный 2,4%, дает отправную точку: теперь мы знаем, что нужно бета-распределение со средним значением примерно 0,024. (Среднее значение бета-распределения составляет α/(α + β).) Однако это все еще оставляет возможные варианты: Beta(1,41), Beta(2,80), Beta(5200), Beta(24 976) и т. д. Итак, что же из этого нужно использовать? Изобразим некоторые из них на графике (рис. 14.3).

Как видите, чем меньше α + β, тем шире распределение. Проблема заключается в том, что даже самый свободный вариант, который мы имеем, Beta(1,41), кажется слишком пессимистичным, так как большая часть плотности вероятности помещается в очень низкие значения. Но мы будем придерживаться этого распределения, поскольку оно основано на 2,4%-ном коэффициенте конверсии в данных от провайдера и является самым слабым из приоритетов. «Слабая» априорная вероятность означает, что она будет легко переопределена фактическими данными, поскольку мы соберем еще больше информации. Более сильная априорная вероятность, такая как Beta(5200), потребовала бы больше доказательств для изменения (посмотрим, как это будет выглядеть дальше). Решение о том, следует ли использовать строгую априорную вероятность, является оценочным, исходя из того, насколько сильно вы ожидаете, что априорные данные описывают то, что вы делаете в данный момент. Как мы увидим, даже слабый априорный показатель может помочь сделать наши оценки более реалистичными при работе с небольшими объемами данных. Помните, что при работе с бета-распределением можно вычислить апостериорное распределение (сочетание нашей вероятности и априорной вероятности), просто сложив вместе параметры для двух бета-распределений:

			Beta(αапостериорное, βапостериорное) =

= Beta(αправдоподобности + αаприорное, βправдоподобности + βаприорное).
		

Используя эту формулу, мы можем сравнить свои убеждения с априорной вероятностью и без априорной вероятности, как показано на рис. 14.4.

Ого! Выглядит довольно отрезвляюще. Несмотря на то что мы работаем с относительно слабой априорной вероятностью, мы видим, что это оказало огромное влияние на то, что мы считаем реалистичными коэффициентами конверсии.

Обратите внимание, что для правдоподобности без априорных данных мы считаем, что коэффициент конверсии может достигать 80%. Как уже упоминалось, это очень подозрительно; любой опытный маркетолог, работающий с электронной почтой, скажет вам, что 80%-ный коэффициент конверсии — это неслыханно. Добавление априорной вероятности к правдоподобности корректирует наши убеждения, так что они становятся намного более разумными.

Но я все еще думаю, что наши обновленные убеждения немного пессимистичны. Может быть, истинный коэффициент конверсии не равен 40%, но он все же может быть лучше, чем предполагает нынешнее апостериорное распределение.

Как можно доказать, что блог имеет лучший коэффициент конверсии, чем сайты, указанные в данных провайдера, имеющие коэффициент 2,4%? Как бы поступил любой рациональный человек? Предоставил больше данных! Мы ждем несколько часов, чтобы получить больше результатов, и выясняем, что из 100 человек, открывших письмо, 25 перешли по ссылке! Давайте посмотрим на разницу между нашей новой апостериорной вероятностью и правдоподобностью (рис. 14.5).

По мере того как мы продолжаем собирать данные, мы видим, что апостериорное распределение с использованием априорной вероятности начинает смещаться в сторону без априорной вероятности. Априорная вероятность по-прежнему контролирует наши данные, давая более консервативную оценку истинного коэффициента конверсии. Однако при добавлении доказательств к нашей правдоподобности она начинает оказывать большее влияние на то, как выглядят апостериорные убеждения. Другими словами, дополнительные наблюдаемые данные делают то, что и должны: медленно раскачивают наши убеждения, чтобы соответствовать реальности. Так что давайте подождем еще ночь и вернемся, имея на руках еще больше данных!

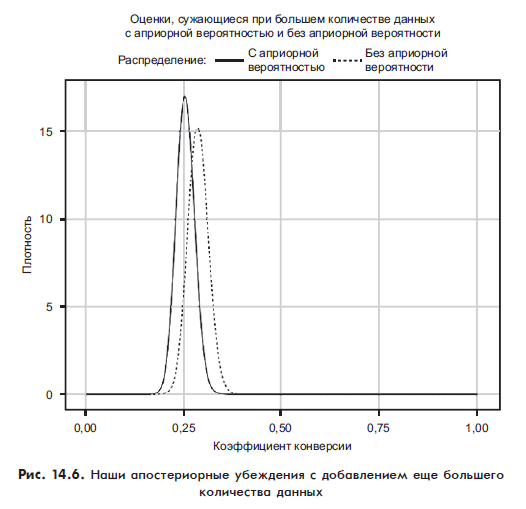
Утром мы видим, что 300 подписчиков открыли письма и 86 из них нажали на ссылку. На рис. 14.6 показаны наши обновленные убеждения.

То, что мы наблюдаем здесь, является наиболее важным моментом в байесовской статистике: чем больше данных собирается, тем больше наши априорные убеждения уменьшаются в результате доказательств. Когда у нас почти не было доказательств, наша вероятность предложила некоторые варианты, которые, как мы знаем, абсурдны (например 80% переходов) как интуитивно, так и из личного опыта. В свете небольшого количества доказательств наши априорные убеждения опровергли все имеющиеся данные.

Но по мере того как мы продолжаем собирать данные, которые не согласуются с априорными вероятностями, последующие убеждения смещаются в сторону того, что говорят нам собранные данные, и отходят от первоначальной априорной вероятности.

Другим важным выводом является то, что мы начали с довольно слабой априорной вероятности. Даже тогда, после всего лишь одного дня сбора сравнительно небольшого набора данных, мы смогли найти апостериорную вероятность, которая кажется гораздо более разумной.

Распределение априорных вероятностей в этом случае очень помогло сделать оценку намного более реалистичной при отсутствии данных. Это априорное распределение вероятностей было основано на реальных данных, поэтому мы могли быть вполне уверены, что оно поможет приблизить оценку к реальности. Тем не менее во многих случаях никаких данных для сохранения априорных вероятностей обычно нет. Так что же делать?

Априорная вероятность как средство измерения опыта

Поскольку мы знали, что идея 80%-ного коэффициента конверсии смехотворна, то использовали данные провайдера, чтобы составить более точную оценку априорной вероятности. Но даже если бы у нас не было данных, которые могли бы помочь установить априорную информацию, то мы все равно могли бы попросить кого-то, имеющего маркетинговый опыт, помочь сделать хорошую оценку. Например, опытный маркетолог знает, что стоит ожидать, к примеру, около 20% коэффициента конверсии.

Учитывая эту информацию от опытного профессионала, можно выбрать относительно слабую априорную вероятность, такую как Beta(2,8), чтобы предположить, что ожидаемый коэффициент конверсии должен составлять около 20%. Это распределение является лишь предположением, но важно то, что мы можем количественно оценить это предположение. Почти для каждого бизнеса эксперты часто могут предоставить мощную априорную информацию, основанную просто на предыдущем опыте и наблюдениях, даже если у них нет специальной подготовки по определению вероятности.

Количественно оценивая этот опыт, мы можем получить более точные оценки и посмотреть, как они могут меняться от эксперта к эксперту. Например, если маркетолог уверен, что истинный коэффициент конверсии должен составлять 20%, мы можем смоделировать это убеждение как Beta(200 800). По мере сбора данных мы можем сравнивать модели и создавать несколько доверительных интервалов, которые количественно моделируют любые экспертные убеждения. Кроме того, по мере получения все большего и большего количества информации разница из-за этих априорных убеждений будет уменьшаться.

Более подробно с книгой «Байесовская статистика» можно ознакомиться на сайте издательства.

Для читателей Tproger скидка 25% по купону — Байес.

По факту оплаты бумажной версии книги «Байесовская статистика» на e-mail высылается электронная книга.