Почему дата-сайентисту нужны ещё и графы

На небе только и разговоров что о графах. Говорят, что их сложно и скучно учить, но зато используют в таких задачах, с которыми классические методы анализа данных не справляются. Давайте разбираться, в каких именно и почему не стоит игнорировать графы, даже если вы новичок в Data Science.

Александр Тюрин

Директор по разработке моделей Управления алгоритмов машинного обучения Газпромбанка

И что это такое — графы?

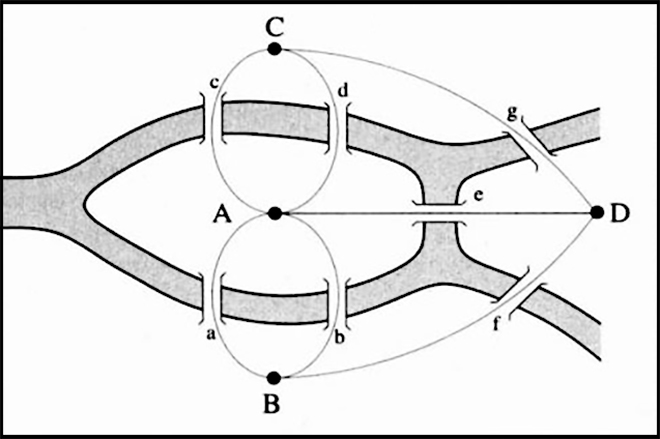
Графы — это абстракция, которую используют для выявления связей между сущностями: множество вершин и множество рёбер, которые их соединяют. Впервые теорию графов применил Леонард Эйлер для решения задачи о Кёнигсбергских мостах. Нужно было найти такой маршрут, чтобы пройти по всем семи сооружениям только один раз и вернуться в исходную точку. С помощью теории графов Эйлер доказал, что это невозможно.

Нагляднее всего оказалось строить маршрут в виде точек (вершин), которые попарно связаны между собой путями (рёбрами). Источник: https://math.stackexchange.com/questions/1173328/eulers-solution-of-seven-bridges-of-königsberg-in-layman-terms

А они вообще востребованы?

Способов анализа структурированных данных становится недостаточно, чтобы делать глубокие предсказания. Если для расчёта спроса и предложения товаров хватит классических методов вроде статистических функций, то для рекомендаций этих товаров можно применять больше действенных методов, в том числе и графы. Поэтому их используют чаще, нежели лет пять назад.

Компании вроде Uber, Google, Pinterest переходят на графы, мотивируя это тем, что производительность таких методов выше, по сравнению с другими современными ИИ-архитектурами. А по прогнозам Gartner к 2025 году графы будут использоваться в 80% инноваций в области данных и аналитики по сравнению с 10% в 2021 году.

Стоит оговориться: графы всё ещё достаточно узкопрофильное направление и используют их не повсеместно. Но дополнительный скил точно не будет лишним — появится больше сфер, в которых можно работать.

И какие задачи можно решать графами?

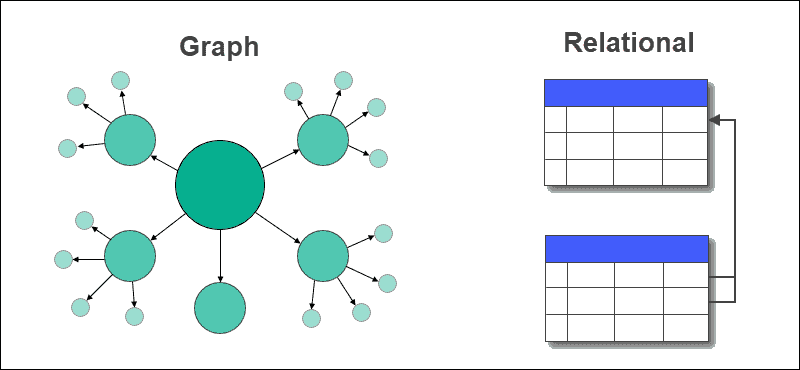
Графы помогают работать с нелинейными данными, которые сложно структурировать в табличный формат и выгоднее представлять в виде связей между объектами — то есть между вершинами через рёбра. Тогда получается сетка, похожая на карту дорог.

Сравнение графовой и реляционной (табличной) баз данных. Источник: https://phoenixnap.com/kb/graph-database

Графы и нейронные сети на их основе используют, например, в биологии. С их помощью биологические сущности (белки, РНК, химические соединения) можно представить в виде «сетки», определить, как они связаны между собой, предсказать новые взаимодействия между ними или свойства.

Здесь можно почитать про графовые методы в биологии.

Рекомендовать товар или друзей

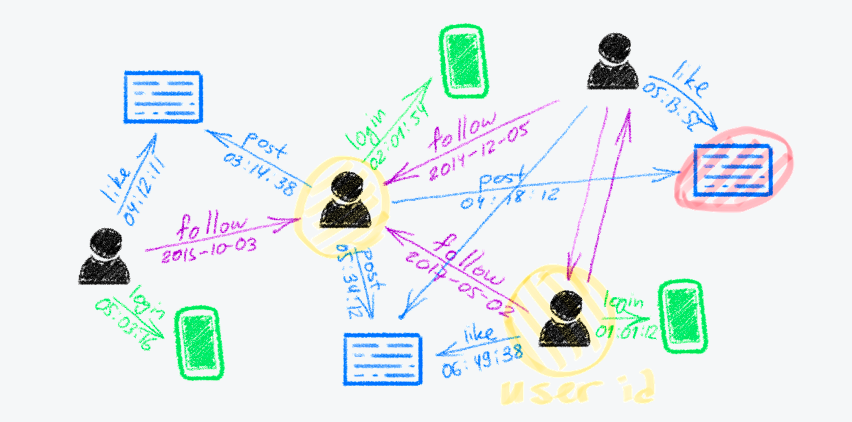
В Газпромбанке есть граф для выявления групп людей со схожими интересами. Он помогает идентифицировать паттерн поведения клиентов, исходя из которого мы предполагаем, какие приложения будут им наиболее полезны. Например, ведут они активный образ жизни, занимаются спортом — значит, порекомендуем похожие спортивные товары.

Схожая механика используется в социальных сетях и дейтинговых приложениях — для рекомендаций друзей и хранения данных, которые генерируют пользователи.

Можно обойтись и без графов: самостоятельно придумать критерии и прописать алгоритм, который будет высчитывать количество взаимодействий между людьми. Но это долго, дорого, ресурсозатратно и есть риск упустить что-то важное, но неочевидное. Графы же позволяют использовать данные сами по себе, любое взаимодействие уже даёт информацию, которую можно анализировать и потенциально применить для решения задач.

С помощью графов можно быстрее сформировать и проанализировать рекомендации, а также легче их представить: два человека — узла — пообщались, то есть между ними выстроилась связь — ребро. В реляционных базах данных хранить такие сети взаимодействий неудобно.

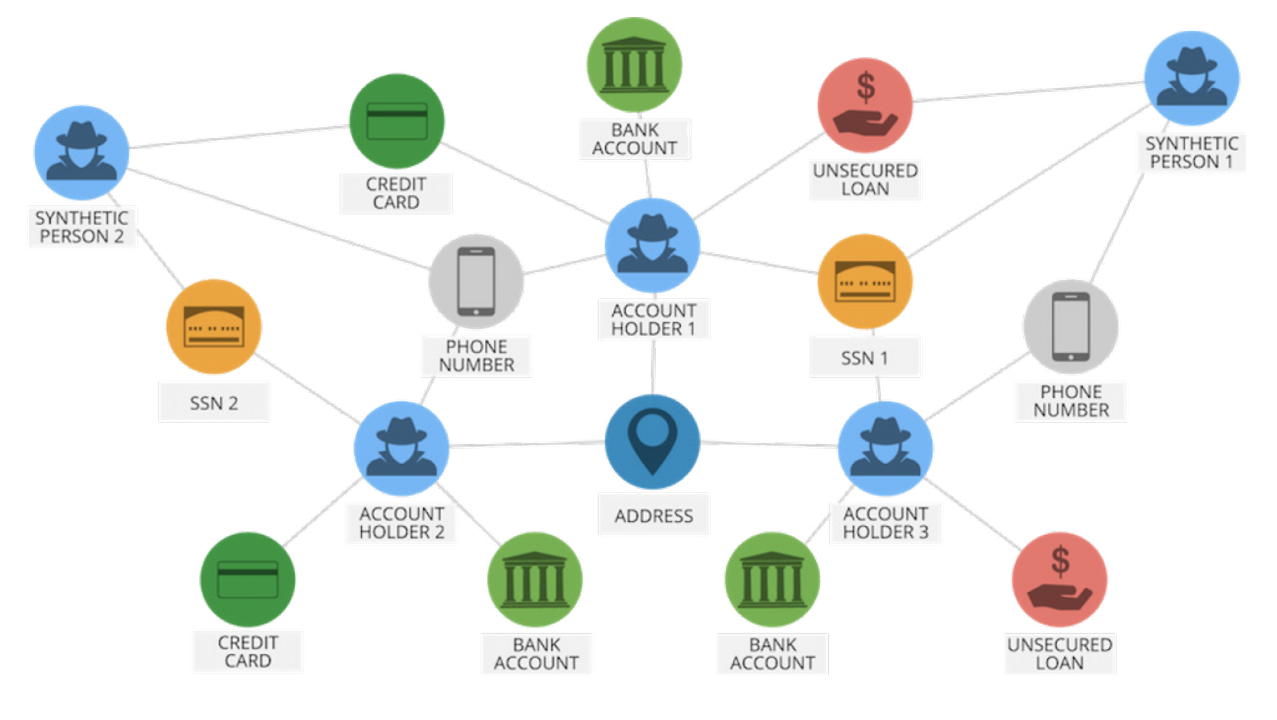
Выявлять мошенничество

Можно построить цепочку транзакционной активности: человек А перевёл деньги человеку B, а тот — человеку C. Если в этой схеме появляется лицо, которое занесено в чёрный список, то мы идентифицируем её как фрод. То есть если в длинной цепочке переводов один из узлов замечен в мошенничестве, то стоит обратить на неё пристальное внимание.

Зачастую мошенники, когда берут кредиты и хотят оформить банкротство, чтобы их не платить, используют разные адреса, номера телефонов, паспортные данные. Или меняют их незначительно, чтобы исправления не были заметны сразу. И то, и то можно назвать подозрительной активностью.

Сложно самостоятельно просчитать наперёд и учесть в алгоритмах, что у человека сегодня одни паспортные данные, а завтра другие. Для графа это не нужно прописывать: он проскорит и зафиксирует людей с такой подозрительной активностью самостоятельно.

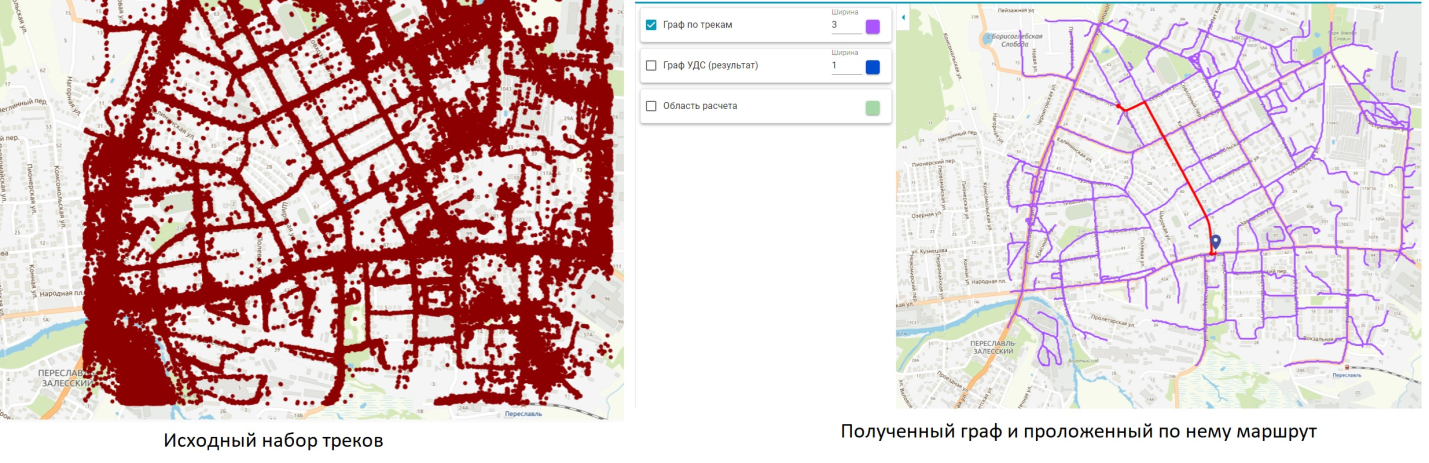
Строить маршруты

С помощью графа можно найти самый короткий и быстрый маршрут из точки А в точку B. Он будет учитывать не только длину дорог, но и поможет предсказать, где и когда трафик меньше.

Рёбра в данном случае — это изменяющиеся величины, которые отражают и учитывают, где, например, ночью дороги пустые, а где в шесть утра пробки и аварии, которые надо объехать. Источник: http://www.geocenter-consulting.ru/news/item/259

Ранжировать информацию по достоверности

В Google графы использовали для ранжирования веб-страниц. Чтобы самый полезный сайт поставить на первое место, придумали алгоритм PageRank.

Каждый сайт был узлом, а ссылки на другие сайты внутри — связями. За счёт этого сайт, который ссылался на более достоверные источники, оказывался выше. Например, если одна из страниц ссылалась на сайт правительства Соединённых Штатов, а другая — на жёлтую прессу, вторая уходила вниз в поисковой выдаче.

Сейчас используют и другие алгоритмы, тот же GPT, но в начале 2000-х Google выстрелил благодаря графам, которые качественнее определяли «авторитетность».

Хранить взаимосвязи между сущностями

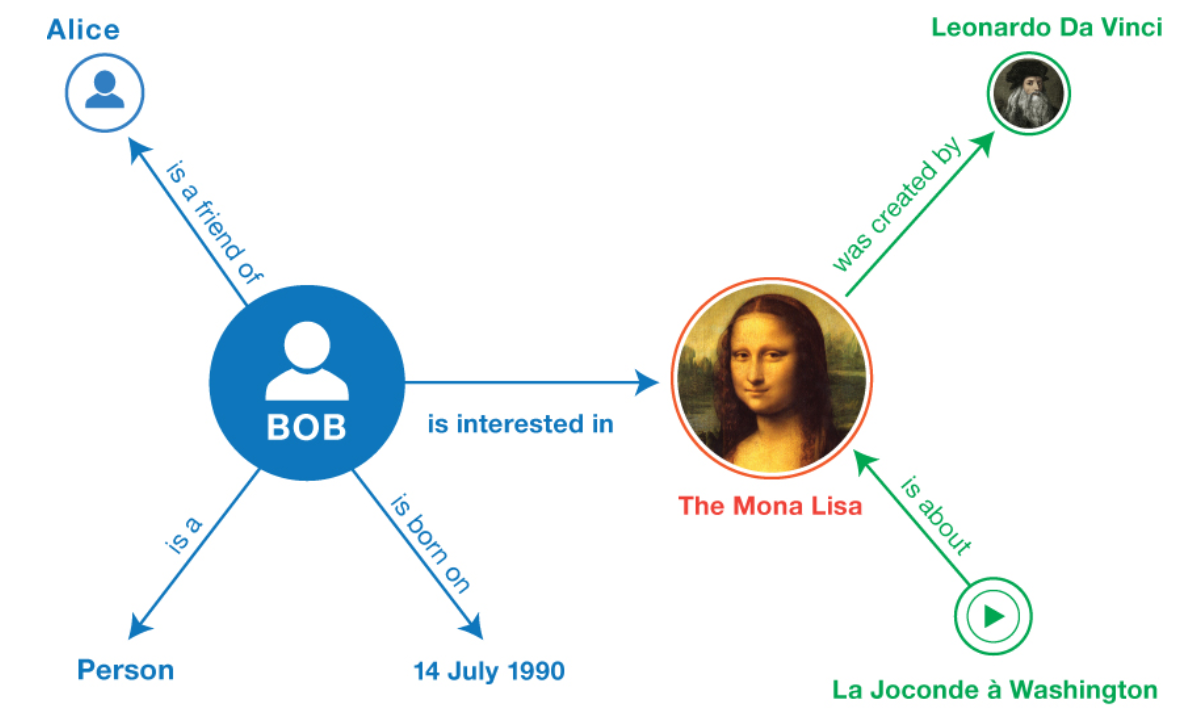
Ещё одна важная предметная область, где применяются графы — графы знаний. Это семантическая структура, в которой хранится информация о разных сущностях и взаимосвязях между ними. Вершиной‎ графа может быть как абстрактное понятие (например, концепция), так и материальный объект (например, предмет или человек).

На основе графов знаний работают, например, голосовые помощники — Alexa от Amazon.

Так могут выглядеть взаимосвязи в графах знаний:

Звучит интересно. А сложно их учить?

Действительно, графы — универсальный и многогранный инструмент, который используется для решения самых разных задач. Держать в голове весь их функционал довольно сложно. Для начала достаточно понимать, что из себя представляют графы и в каких предметных областях они применяются. А далее изучать конкретные алгоритмы и инструменты в зависимости от задачи.

Где можно узнать о них подробнее?

• ТГ-канал про графы: @sberlogawithgraphs
• Курс Стэнфордского университета
• Книга «Введение в теорию графов» Р. Уилсона
• Книга про графовые нейронные сети: Graph Representation Learning. William L. Hamilton