Применение нормального распределения для прогнозирования результативности в Scrum

В современном мире, где программное обеспечение становится основополагающим элементом практически каждого бизнес-процесса, способность точно прогнозировать временные рамки и результаты разработки ПО становится критически важной. Однако динамичная природа проектов по разработке программного обеспечения часто приводит к значительным колебаниям в производительности и прогрессе, что затрудняет точное прогнозирование результатов.

Применяя концепции и методологии, зародившиеся в теории вероятностей и статистическом анализе, давайте попробуем понять, как нормальное распределение (также известное как распределение Гаусса) может быть использовано для моделирования и анализа производительности разработки (velocity) в методологиях Agile и Scrum, а конкретно – предположить результат, который команда сможет получить в будущем. Но так же понять, является ли полученный результат нормой или есть отклонения, на которые команда должна реагировать.

Эта статья будет полезна как новичкам, так и опытным специалистам в области управления проектами по разработке ПО, предоставляя им новые инструменты и перспективы, необходимые для достижения успеха в постоянно меняющемся и высоко конкурентном технологическом мире.

Для наших изысканий возьмем реальные данные из одного моего реального проекта и его реальных результатов.

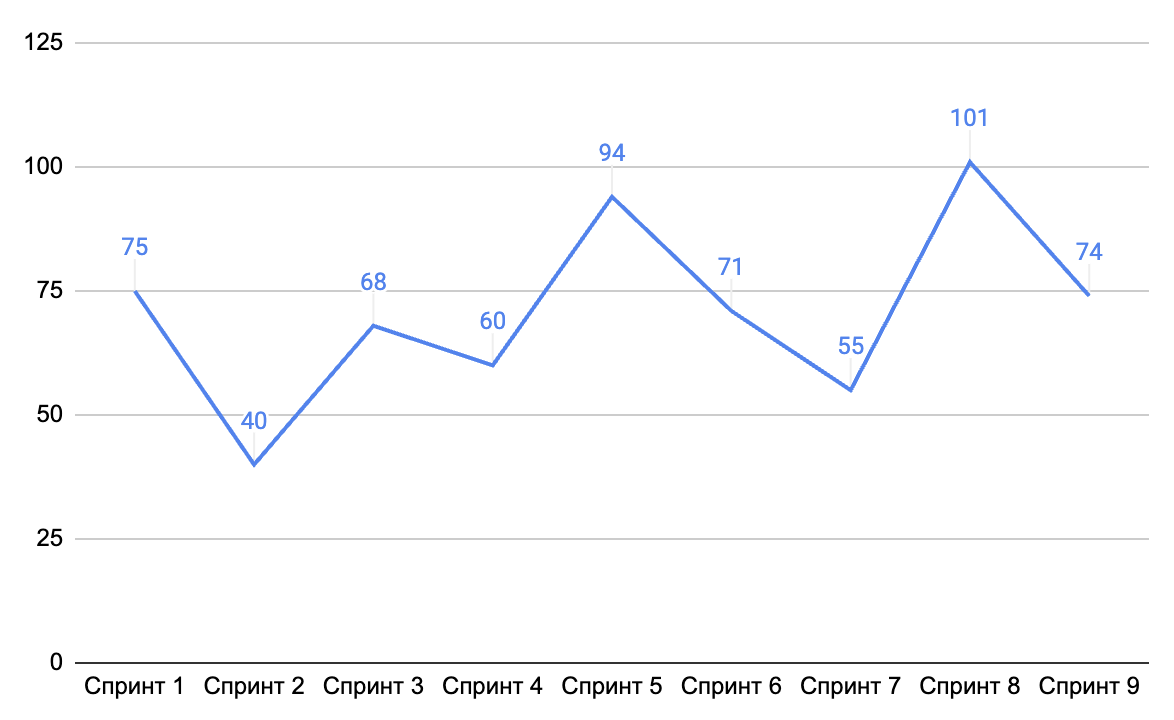
У нас имеется результаты последних спринтов в Story Points:

			75 40 68 60 94 71 55 101 74 13 183
		

Давайте попробуем рассчитать среднее отклонение от нормы. То есть поймём, при каких результатах спринта нам надо задуматься и постараться понять есть ли проблема и в чем она состоит, а при каких результатах у нас все хорошо в работе команды.

Для прогнозирования результатов следующих спринтов на основе нормального распределения, нам необходимо провести статистический анализ имеющихся данных и использовать эти параметры для создания прогноза. Давайте разберем этот процесс пошагово.

Для начала представим наши результаты в таблице и на графике:

1. Спринт 1 – 75.
2. Спринт 2 – 40.
3. Спринт 3 – 68.
4. Спринт 4 – 60.
5. Спринт 5 – 94.
6. Спринт 6 – 71.
7. Спринт 7 – 55.
8. Спринт 8 – 101.
9. Спринт 9 – 74.
10. Спринт 10 – 13.
11. Спринт 11 – 183.

При анализе данных, особенно если они содержат экстремальные значения (как, например, 13 или 183 в вашем наборе данных), важно рассмотреть, не являются ли эти точки выбросами, вызванными необычными обстоятельствами, и не должны ли они быть исключены из анализа.

Для расчета стандартного отклонения без учета экстремальных значений, нам нужно сначала идентифицировать, какие значения можно считать экстремальными. В контексте вашего набора данных, значения, такие как “13” и “183”, кажутся аномально низким и высоким соответственно. Давайте исключим их из наших расчетов.

Далее нам нужно пересчитать среднее значение без учета этих экстремальных значений. У нас есть следующие значения: 75, 40, 68, 60, 94, 71, 55, 101, 74 (исключены “13” и “183”).

Подсчитаем среднее:

			Среднее = (75+40+68+60+94+71+55+101+74) / 9 ≈ 70.89.
		

Теперь вычислим квадраты отклонений от среднего и найдем их сумму:

			(75 - 70.89)^2 + (40 - 70.89)^2 + (68 - 70.89)^2 + (60 - 70.89)^2 + (94 - 70.89)^2 + (71 - 70.89)^2 + (55 - 70.89)^2 + (101 - 70.89)^2 + (74 - 70.89)^2
		

Проведем подсчет:

			(4.11)^2 + (-30.89)^2 + (-2.89)^2 + (-10.89)^2 + (23.11)^2 + (0.11)^2 + (-15.89)^2 + (30.11)^2 + (3.11)^2 = 16.89 + 954.59 + 8.35 + 118.59 + 534.07 + 0.0121 + 252.39 + 906.63 + 9.67 = 2801.1681
		

Таким образом, сумма квадратов отклонений для данного набора данных (исключая экстремальные значения) составляет примерно 2801.17.

Теперь найдем исправленную дисперсию – среднюю сумма квадратов отклонений каждого значения от среднего значения. Мы уже вычислили сумму квадратов отклонений. Теперь, чтобы найти дисперсию, нам нужно разделить эту сумму на количество наблюдений.

Из предыдущих расчетов у нас есть:

• Сумма квадратов отклонений: 2801.17.
• Количество наблюдений (N): 9 (поскольку мы исключили два экстремальных значения).

			Дисперсия=Сумма квадратов отклонений / N =2801.17 / 9≈311.24
		

Таким образом, дисперсия для данного набора данных составляет примерно 311.24.

Стандартное отклонение является мерой разброса значений относительно среднего значения (математического ожидания) и вычисляется как квадратный корень из дисперсии. Таким образом, стандартное отклонение для вашего набора данных составляет примерно 17.64. Это значит, что в среднем значения отклоняются от среднего (70.89) на 17.64 единицы.

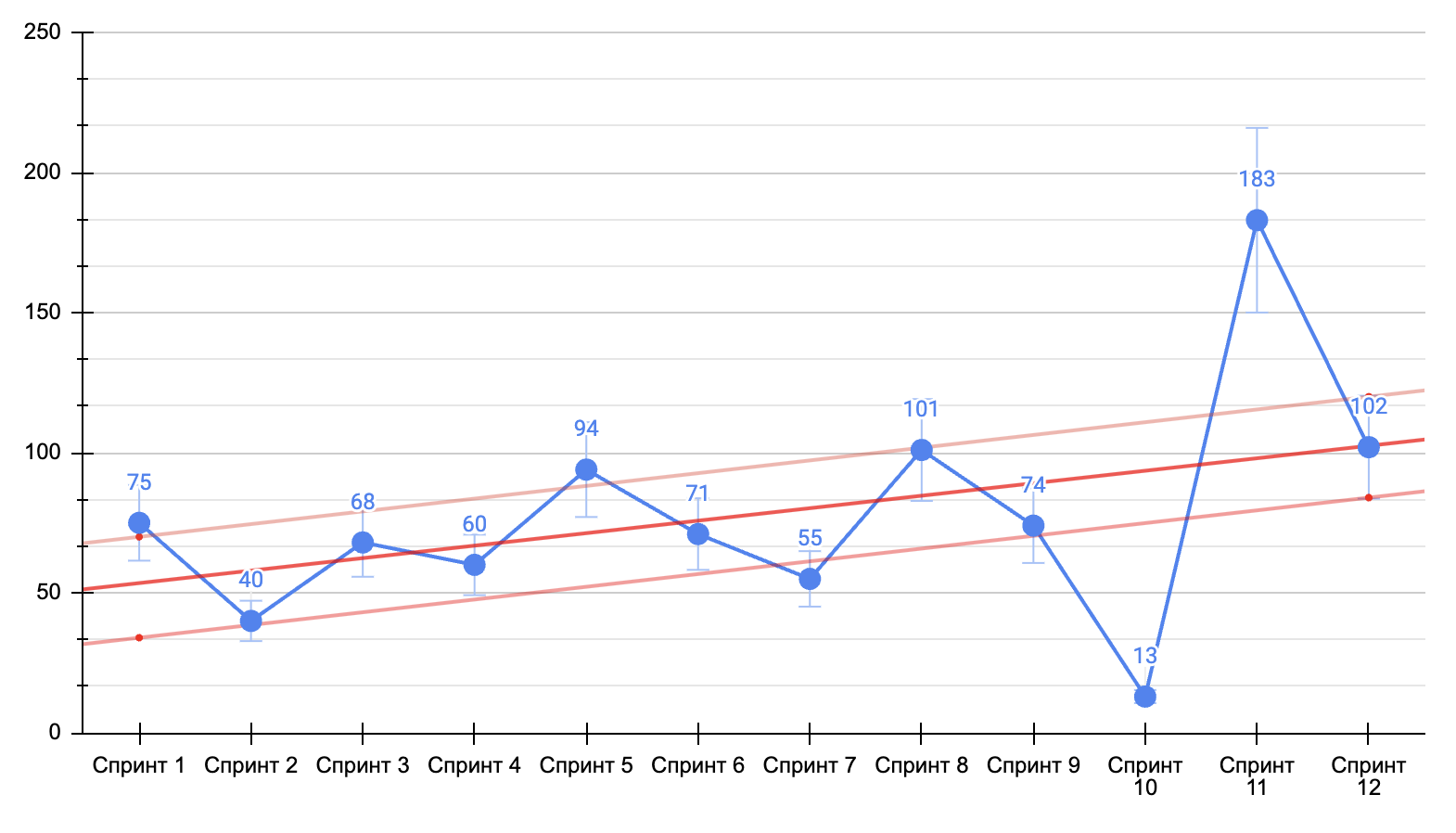
Теперь давайте сделаем наложим тренд (красная линия) на наш график с учетом всех спринтов и попытаемся предсказать результат следующего спринта

Выходит мы можем ожидать результатом следующего спринта примерно 102 SP. Давайте учетом того, что стандартное отклонение для вашего набора данных составляет примерно 17.64 наш нормальный результат, округленный до целых SP, который будет в пределах нормы составит 84-120 SP.

Применив математический анализ, мы смогли предсказать результат нашего следующего спринта с учетом данных за прошлый период и добавить к ним возможную погрешность, которая является нормой.