Python vs C++: какой язык быстрее найдет все простые числа до миллиарда

для

Рассказываем, какие есть алгоритмы для поиска простых чисел и реализуем наиболее популярный и простой на Python и C++.

486 открытий2К показов

Баттлы языков — извечная тема, которая никогда себя не изживет. Понятно, что язык программирования нужно выбирать под конкретные цели. Но если мы только учимся, можно попробовать решить какую-нибудь задачку с помощью двух разных инструментов — хотя бы для того чтобы понять, какой нравится больше.

Сегодня будем искать все простые числа до миллиарда с помощью кода на Python и C++. Если вы думаете, что результат совсем очевиден, то это не так.

Напоминание: простые числа — те, которые имеют два различных делителя. Простыми словами, они делятся только сами на себя и на единицу. Например: 2, 3, 5, 7 и так далее.

Для начала: быстро окунемся в математику

Есть несколько алгоритмов, которые помогут найти все простые числа до N. Это материал для отдельной статьи, поэтому пробежимся по основным.

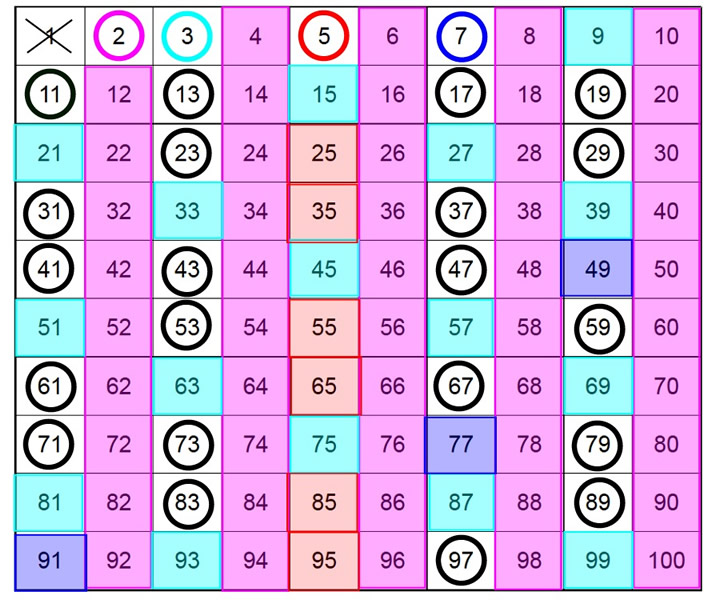
Решето Эратосфена

Один из самых древних и известных алгоритмов, чтобы найти простые числа до N. Плюс он понятный, не занимает слишком много памяти (если речь не идет об очень больших N). Работает так:

Создается список чисел от 2 до N.
Все кратные числа кратные 2 (4, 6, 8, ...) помечаются как составные.
Переходим к 3 и вычеркиваем все числа, кратные ему.
То же самое повторяем со всеми числами из списка до N
Так до тех пор, пока не проверятся все числа до N.

Python vs C++: какой язык быстрее найдет все простые числа до миллиарда 1

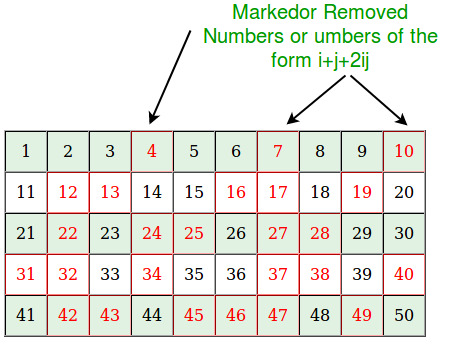
Решето Сундарама

Этот алгоритм работает немного по другой логике:

Создается список чисел от 1 до (N-1)/2.
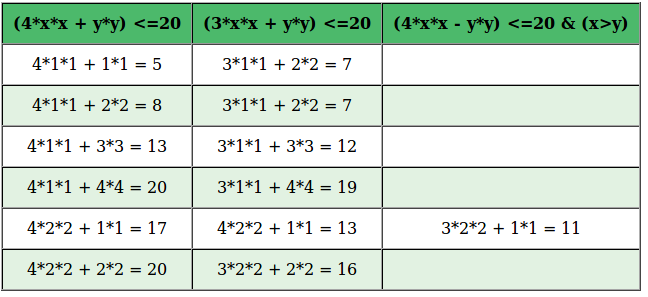
Исключаются числа типа i + j + 2ij, где i и j — натуральные числа, и i <= j.
Оставшиеся числа умножаются на 2 и увеличиваются на 1 — так получаем простые числа.

Python vs C++: какой язык быстрее найдет все простые числа до миллиарда 2

Этот алгоритм занимает меньше памяти, чем решето Эратосфена, поскольку работает только с половиной диапазона. Но при этом он сложнее в плане понимания и реализации.

Решето Аткина

Это уже современный алгоритм (появился в начале 21 веке). Он использует более сложные математические концепции и работает так:

Создается список чисел от 1 до N.
Используются квадратичные формы, чтобы предварительно отсеять составные числа.
Затем составные числа просеиваются финально для полного исключения.

Python vs C++: какой язык быстрее найдет все простые числа до миллиарда 3

Решето Аткина более эффективно, когда речь идет об огромных числах, по сравнению с первыми двумя алгоритмами. Оно тоже не простое в реализации, плюс может быть медленнее при работе с небольшим N.

Это три основных алгоритма для поиска простых чисел до N. Сейчас существуют различные оптимизации этих методов, например, колесная факторизация (оптимизированный алгоритм Эратосфена).

Ищем простые числа до миллиарда на Python и C++

Python — не самый быстрый язык для таких операций. Если не использовать библиотеки, то программа выдает ограничение и не может завершиться. Например, вот код на чистом Питоне с алгоритмом Эратосфена:

			import time

def sieve_of_eratosthenes(limit):
    sieve = [True] * (limit + 1)
    sieve[0] = sieve[1] = False
    # Реализуем решето
    for i in range(2, int(limit**0.5) + 1):
        if sieve[i]:
            sieve[i*i : limit+1 : i] = [False]*len(sieve[i*i : limit+1 : i])
    return [i for i, is_prime in enumerate(sieve) if is_prime]

start_time = time.time()

limit = 100_000_000
primes = sieve_of_eratosthenes(limit)

print(f"Найдено {len(primes)} простых чисел до {limit}")
print(f"Время выполнения: {time.time() - start_time:.4f} секунд")

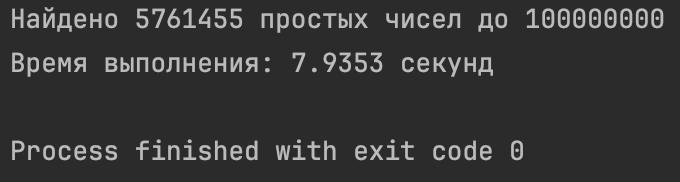
PyCharm с ограничением 1 000 000 000 не завершает программу. Если же поставить лимит = 100 000 000, то получим такой результат (почти 8 секунд!):

Python vs C++: какой язык быстрее найдет все простые числа до миллиарда 4

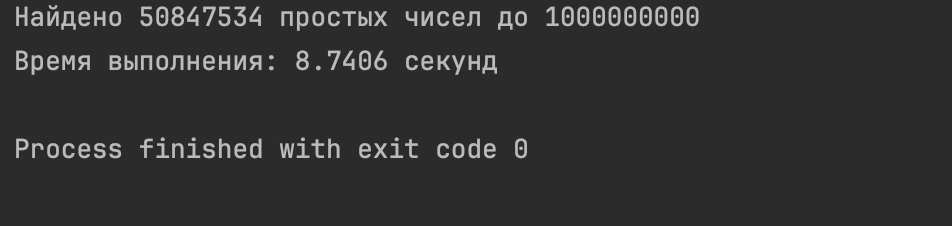
Теперь попробуем проделать то же самое с библиотекой numpy, которая как раз подходит для работы с большими числами:

			import numpy as np
import time

def sieve_of_eratosthenes(limit):
    # массив, где все числа простые
    sieve = np.ones(limit, dtype=bool)
    sieve[0] = sieve[1] = False
    # решето
    for i in range(2, int(np.sqrt(limit)) + 1):
        if sieve[i]:
            sieve[i*i:limit:i] = False
    return np.where(sieve)[0]
    
start_time = time.time()

limit = 1_000_000_000
primes = sieve_of_eratosthenes(limit)

print(f"Найдено {len(primes)} простых чисел до {limit}")
print(f"Время выполнения: {time.time() - start_time:.4f} секунд")

Результат будет таким:

Python vs C++: какой язык быстрее найдет все простые числа до миллиарда 5

Учитывайте, что мы искали здесь числа до миллиарда!

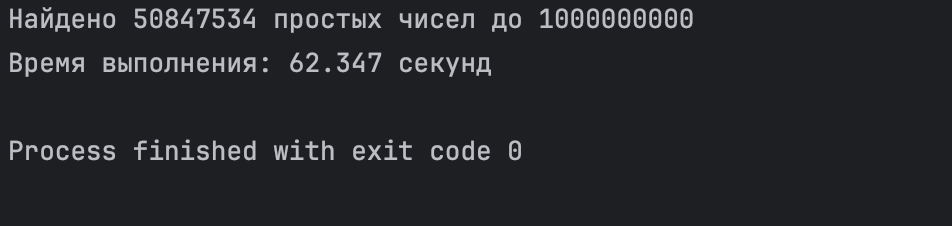
Давайте попробуем сделать то же самое на С++:

			#include <iostream>
#include <vector>
#include <cmath>
#include <chrono>

std::vector<int> sieve_of_eratosthenes(int limit) {
    std::vector<bool> sieve(limit, true);
    
    if (limit > 0) sieve[0] = false;
    if (limit > 1) sieve[1] = false;
    
    for (int i = 2; i <= std::sqrt(limit); i++) {
        if (sieve[i]) {
            for (int j = i * i; j < limit; j += i) {
                sieve[j] = false;
            }
        }
    }
    
    std::vector<int> primes;
    for (int i = 0; i < limit; i++) {
        if (sieve[i]) {
            primes.push_back(i);
        }
    }
    
    return primes;
}

int main() {
    const int limit = 1'000'000'000;
    
    auto start_time = std::chrono::high_resolution_clock::now();
    
    std::vector<int> primes = sieve_of_eratosthenes(limit);
    
    auto end_time = std::chrono::high_resolution_clock::now();
    auto duration = std::chrono::duration_cast<std::chrono::milliseconds>(end_time - start_time);
    
    std::cout << "Найдено " << primes.size() << " простых чисел до " << limit << std::endl;
    std::cout << "Время выполнения: " << duration.count() / 1000.0 << " секунд" << std::endl;
    
    return 0;
}

Эта программа будет выполняться больше минуты:

Python vs C++: какой язык быстрее найдет все простые числа до миллиарда 6

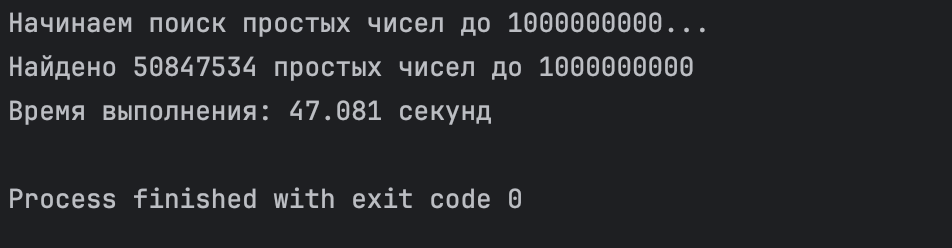
Чтобы оптимизировать программу, можно использовать сегментированное решето Эратосфена:

			#include <iostream>
#include <vector>
#include <cmath>
#include <chrono>

// используем сегментированное решето и более компактное хранение для больших чисел
void segmented_sieve(uint64_t limit, uint64_t& count) {
    const uint64_t segment_size = 1 << 20; // ~1 МБ для компактности в кэше

    uint64_t sqrt_limit = static_cast<uint64_t>(std::sqrt(limit)) + 1;

    std::vector<bool> is_prime(sqrt_limit + 1, true);
    is_prime[0] = is_prime[1] = false;

    // ищем все простые числа до sqrt_limit
    for (uint64_t i = 2; i * i <= sqrt_limit; i++) {
        if (is_prime[i]) {
            for (uint64_t j = i * i; j <= sqrt_limit; j += i) {
                is_prime[j] = false;
            }
        }
    }

    // собираем малые простые числа
    std::vector<uint64_t> small_primes;
    for (uint64_t i = 2; i <= sqrt_limit; i++) {
        if (is_prime[i]) {
            small_primes.push_back(i);
            count++; 
        }
    }

    std::vector<bool> block(segment_size);

    uint64_t low = sqrt_limit + 1;
    while (low <= limit) {
   
        uint64_t high = std::min(low + segment_size - 1, limit);

        std::fill(block.begin(), block.end(), true);

        for (uint64_t prime : small_primes) {
            // находим первое кратное простого числа в текущем сегменте
            uint64_t start = std::max(prime * prime, (low + prime - 1) / prime * prime);

            // отмечаем все кратные этого простого числа в текущем сегменте
            for (uint64_t j = start; j <= high; j += prime) {
                block[j - low] = false;
            }
        }

        // подсчитываем простые числа в текущем сегменте
        for (uint64_t i = 0; i < high - low + 1; i++) {
            if (block[i]) {
                count++;
            }
        }
        // следующий сегмент
        low += segment_size;
    }
}

std::vector<uint64_t> get_first_n_primes(uint64_t n) {
    std::vector<uint64_t> primes;
    primes.reserve(n);

    primes.push_back(2);

    for (uint64_t i = 3; primes.size() < n; i += 2) {
        bool is_prime = true;
        for (uint64_t j = 0; j < primes.size() && primes[j] * primes[j] <= i; j++) {
            if (i % primes[j] == 0) {
                is_prime = false;
                break;
            }
        }
        if (is_prime) {
            primes.push_back(i);
        }
    }

    return primes;
}

int main() {
    const uint64_t LIMIT = 1000000000;

    auto start_time = std::chrono::high_resolution_clock::now();

    uint64_t count = 0;
    segmented_sieve(LIMIT, count);

    auto end_time = std::chrono::high_resolution_clock::now();
    auto duration = std::chrono::duration_cast<std::chrono::milliseconds>(end_time - start_time);

    std::cout << "Найдено " << count << " простых чисел до " << LIMIT << std::endl;
    std::cout << "Время выполнения: " << duration.count() / 1000.0 << " секунд" << std::endl;
    

    return 0;
}

Время выполнения уменьшилось на 20 секунд:

Python vs C++: какой язык быстрее найдет все простые числа до миллиарда 7

Итоги

В нашей задачке numpy действительно может оказаться быстрее, чем обычная реализация на C++. На то есть несколько причин:

Если в NumPy используется эффективный векторизованный алгоритм — в нашем случае решето Эратосфена, — преимущества SIMD-операций (одновременное выполнение одной операции над множеством данных) могут сильно ускорить вычисления.
Неоптимизированная реализация решета на C++ с обычными циклами может быть медленнее оптимизированной векторизованной реализации в NumPy.
NumPy использует внутренне оптимизированные C/C++ библиотеки, в которых есть куча оптимизаций для работы с массивами.

Но эффективно оптимизированный код на C++ (например, с использованием SIMD-инструкций, оптимизации кэш-памяти, параллелизма) почти всегда будет быстрее любой реализации на Python/numpy. Правда, такой код будет занимать сотни строк.

Производительность зависит от конкретных алгоритмов, поэтому так себе метод на C++ проиграет хорошему на numpy. Во многих задачах по работе с большими данными плюсы будут более быстрыми, но для типичного пользования numpy — отличная альтернатива.

486 открытий2К показов

Также рекомендуем

На улице ML-специалистов праздник: состоялся крупнейший апдейт NumPy за последние 18 лет

Команда NumPy выпустила релиз под версией 2.0.0 — первый мажорный релиз с 2006 года. Новых возможностей появилось немерено

«Хаос и беспорядок»: эксперт назвал минусы микросервисной архитектуры

Микросервисы — это не всегда решение. Эксперт разобрал главные минусы: хаос в архитектуре, рост затрат, сложная отладка и непредсказуемость системы

Как работают управляющие конструкции в Python: if, else, match, for, while

Управляющие конструкции в программировании. Показываем, как работают if, else, switch, for, while. Рассматриваем пошаговую инструкцию и практические примеры ✔ Tproger

Вышла Visual Studio Code 1.93: поддержка профилей, улучшенная работа с Python и прочие нововведения

Visual Studio Code версии 1.93 представила множество нововведений, включая редактор профилей для переключения между различными наборами настроек, что особенно полезно для разработчиков с разными рабочими процессами. Также улучшена поддержка Python, добавлена возможность работы с тестами Django, и улучшена отладка