Сравниваем LLM-модели, чтобы потом внедрить без мороки

В основе LLM-моделей (англ. «модель большого языка») лежит фундаментальная цель прогнозирования. Исходя из контекста, они предсказывают следующие слова. Их еще называют стохастическими («вероятностными») попугаями.

Такой навык неоценим при генерации текста и решении всевозможных задач. Врожденная креативность таких «учеников» открывает море возможностей для контент-мейкеров, предлагая им источник вдохновения и помощь.

Моделей уже собралась целая коллекция — почти 30 штук (рейтинг на sapling.ai). Не только лишь Яндекс может составить OpenAI конкуренцию. Давайте сравним некоторые популярные решения с точки зрения разработчиков-внедренцев.

Мировое сообщество постоянно создает передовые языковые решения. Число параметров (считай, способностей оперировать словами, аббревиатурами и словосочетаниями) перевалило у некоторых за 1,5 триллиона единиц, модели стали демонстрировать «побочные эффекты»: резюмирование текста, разъяснения шуток, автодополнение кода и многое другое.

В качестве метрик для сравнения буду использовать:

• Количество тредов на StackOverflow;
• Объем параметров;
• Цена 1К токенов для малых проектов;
• Наличие условно бесплатного тарифа;
• Доступность гражданам РФ (усложнен ли деплой после ввода санкций);
• Способность решить математическую задачу.

GPT-4

Уволив и вернув Сэма Альтмана, OpenAI обратили внимание общественности на раскол мировоззрений: даже среди технических евангелистов есть лагеря оптимистов и пессимистов. Дело не столько в вере в скорейшую сингулярность с роботами-медсестрами, излечением деменции мозговыми чипами и полноценными виртуальными собеседниками. Люди сомневаются, успеют ли дожить до такого.

Среди всех моделей эта самая обсуждаемая, как в новостях, так и на форумах. Число тредов на StackOverflow перевалило за 4500 тысячи, а это много для отдельно взятой технологии. Компания не предлагает бесплатного тарифа для своих пользователей и в целом предлагает достаточно высокий ценник (0,06$ за тысячу токенов – примерно 800 слов)..

Задача:

			Исследуй ряд на сходимость:
\sum_{n=1}^\infty = \frac{n+2}{n^2+n+1}
		

Для начала – решение системы Wolfram Alpha (ряд сходится):

Ответ нейросети:

Если вы хотите познакомиться с API GPT поближе, изучите статью о собственных данных для GPT-4.

Деплоить приложение на GPT-4 в России – задача не для слабонервных по части оплаты. Приходится ехать за границу и создавать юрлицо на территории, скажем, Восточной Европы + банковский счет. Карточки из Казахстана не принимаются.

Google BARD

Примечательно, что модель обладает уникальной способностью генерировать точные и глубокие научные объяснения. BARD превосходно анализирует сложные проблемы и предлагает логические решения. Учебный корпус BARD включает в себя обширный массив текстовых данных — научные работы, книги и статьи. Основная цель ее — связные рассуждения.

Чтобы пообщаться с этой нейросетью, достаточно зайти на bard.google.com с VPN:

Решение задачи:

С оплатой, полагаю, в случае BARD будет также, как и с Google Cloud в целом. Поскольку на момент ввода санкций слишком большое число российских юрлиц пользовались продуктами Google, обходные решения об оплате нашлись довольно быстро, пускай и с огромной комиссией. Дорожку протоптали, и LLM наверняка подключится к той же системе биллинга.

LLaMA

Эта модель демонстрирует впечатляющие мультимодальные возможности, позволяющие ей обрабатывать и генерировать текст в сочетании с другими типами данных — визуальными, слуховыми, LLaMA может создавать более полные и контекстуально соответствующие результаты.

Условия задачи по-русски модель не поняла, потому переформулируем на английский:

			Check this series for convergence:
\sum_{n=1}^\infty = \frac{n+2}{n^2+n+1}
		

Ответ нейросети верный:

			Sure! To check the convergence of the series, we can use the ratio test. 
The ratio test states that if the limit of the ratio of consecutive terms of a 
series is less than 1, then the series converges. If the limit of the ratio is 
greater than or equal to 1, then the series diverges.In this case, the ratio of 
consecutive terms is:

$$\frac{a_n}{a_{n-1}} = \frac{\frac{n+2}{n^2+n+1}}{\frac{n-1+2}{n^2-n+1}} = 
\frac{n+2}{n-1+2}\cdot\frac{n^2-n+1}{n^2+n+1} = \frac{n+2}{n-1+2}\cdot\frac{1 - 
\frac{1}{n}}{1 + \frac{1}{n}}$$

As $n$ approaches infinity, the term $\frac{1}{n}$ approaches 0, so the ratio 
approaches:

$$\lim_{n\to\infty}\frac{a_n}{a_{n-1}} = 
\lim_{n\to\infty}\frac{n+2}{n-1+2}\cdot\lim_{n\to\infty}\frac{1 - \frac{1}{n}}
{1 + \frac{1}{n}} = \frac{1}{1} = 1$$

Since the limit of the ratio is equal to 1, 
we cannot conclude that the series converges or diverges using the ratio test.
		

Помимо теста соотношения (Ratio Test) модель предложила альтернативный метод с неверным выводом.

Эта модель завоевала свое место под солнцем в сообществе экспериментаторов, поскольку предлагает условной бесплатный тариф.

YandexGPT 2

На мой взгляд, этот амбициозный проект вполне сможет перетянуть на себя одеяло на российском рынке. При наличии линейки продуктов Yandex Cloud с бесшовной интеграцией YaLM 2.0 шансы здорово подрастают.

Однако когда сравниваешь модели по числу параметров, отечественные импортозаместители сразу выглядят проигрышно. Не беда, создатели быстро исправляют ошибки и совершенствуют свои детища.

Решение задачи о сходимости верное:

			Для исследования сходимости ряда \sum_{n=1}^{\infty} \frac{n+2}{n^2 + n + 1} мы 
можем применить признак сравнения с другим рядом. Мы хотим сравнить наш ряд с 
рядом, сходимость которого уже известна.

Рассмотрим ряд \sum_{n = 1}^{\infty} \frac{1}{n^2}, который сходится как ряд, квадрат 
гармонического ряда.

Теперь сравним общий член нашего ряда с общим членом ряда \frac{1}{n^2}:
\frac{n + 2}{n^2 + n + 1} > \frac{1}{n^2} при достаточно больших n, потому что 
числитель и знаменатель первого выражения растут быстрее, чем у второго.

Таким образом, наш ряд сходится, так как он меньше сходящегося ряда \sum_{n = 1}
^{\infty}\frac{1}{n^2}.
		

GigaChat

Самая маленькая, если судить по числу параметров, модель: всего 18 млрд. параметров (в 88+ раз меньше GPT-4).

Это решение радует наличием условно бесплатного тарифа, однако малое количество тредов на форумах настораживает. Сама по себе новизна продукта — не проблема, но вероятность выбраться из затыка, если разработчика-предшественник с другого конца планеты уже такое спросил, увеличивается.

К сожалению, GigaChat не справился с задачей на сходимость ряда и даже рассказал о несуществующем тесте Сундарама-Рамануджана:

Заключение

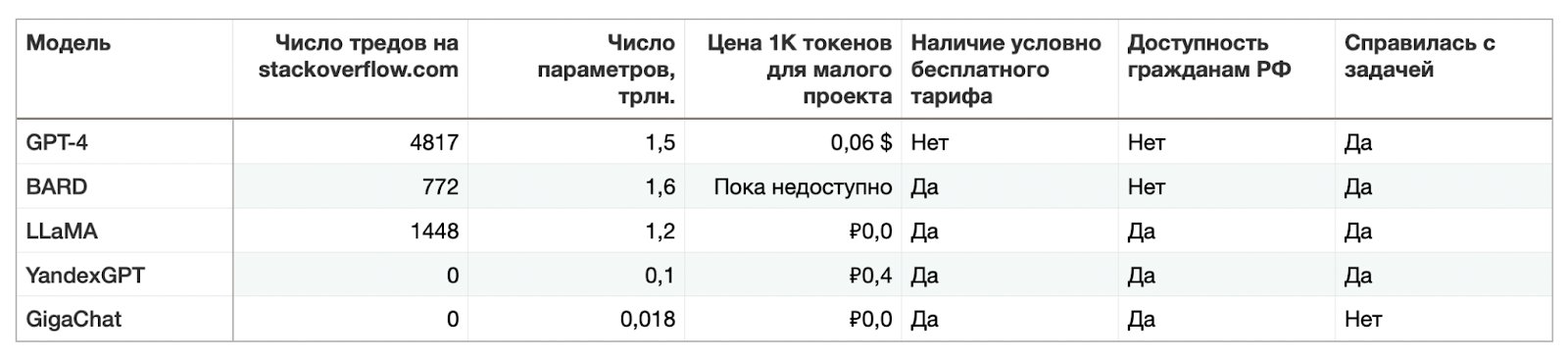
Для вас я свела сравнительные характеристики моделей в таблицу: