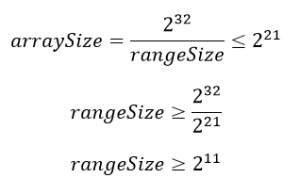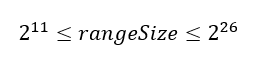Алгоритм, который генерирует целое число, отсутствующее в файле

Дан входной файл, содержащий четыре миллиарда целых 32-битных чисел. Предложите алгоритм, генерирующий число, отсутствующее в файле. Имеется 1 Гбайт памяти для этой задачи. Дополнительно: а что если у вас всего 10 Мбайт? Количество проходов по файлу должно быть минимальным.

В нашем распоряжении 232 (или 4 миллиарда) целых чисел. У нас есть 1 Гбайт памяти, или 8 млрд бит.

8 млрд бит — вполне достаточный объем, чтобы отобразить все целые числа. Что нужно сделать?

1. Создать битовый вектор с 4 миллиардами бит. Битовый вектор — это массив, хранящий в компактном виде булевы переменные (может использоваться как int, так и другой тип данных). Каждую переменную типа int можно рассматривать как 32 бита или 32 булевых значения.
2. Инициализировать битовый вектор нулями.
3. Просканировать все числа (num) из файла и вызвать BV.set(num, 1).
4. Еще раз просканировать битовый вектор, начиная с индекса 0.
5. Вернуть индекс первого элемента со значением 0.

Следующий код реализует наш алгоритм:

			byte[] bitfield = new byte [0xFFFFFFF/8];
void findOpenNumber2() throws FileNotFoundException {
	Scanner in = new Scanner(new FileReader("file.txt"));
	while (in.hasNextInt()) {
		int n = in.nextInt ();
		/* Находим соответствующее число в bitfield, используя
		* оператор OR для установки n-го бита байта
		* (то есть 10 будет соответствовать 2-му биту индекса 2
		* в массиве байтов). */
		bitfield [n / 8] |= 1 << (n % 8);
	}

	for (int i = 0; i < bitfield.length; i++) {
		for (int j = 0; j < 8; j++) {
		/* Получает отдельные биты каждого байта. Когда будет найден
		* бит 0, находим соответствующее значение. */
			if ((bitfield[i] & (1 << j)) == 0) {
				System.out.println(i * 8 + j);
				return;
			}
		}
	}
}
		

Решение для 10 Мбайт памяти

Можно найти отсутствующее число, воспользовавшись двойным проходом по данным. Давайте разделим целые числа на блоки некоторого размера (мы еще обсудим, как правильно выбрать размер). Пока предположим, что мы используем блоки размером 1000 чисел. Так, blоск0 соответствует числам от 0 до 999, block1 — 1000 — 1999 и т.д.

Нам известно, сколько значений может находиться в каждом блоке. Теперь мы анализируем файл и подсчитываем, сколько значений находится в указанном диапазоне: 0-999, 1000-1999 и т.д. Если в диапазоне оказалось 998 значений, то «дефектный» интервал найден.

На втором проходе мы будем искать в этом диапазоне отсутствующее число. Можно воспользоваться идеей битового вектора, рассмотренного в первой части задачи. Нам ведь не нужны числа, не входящие в конкретный диапазон.

Как же выбрать размер блока? Давайте введем несколько переменных:

• Пусть rangeSize — размер диапазонов каждого блока на первом проходе.
• Пусть arraySize — число блоков при первом проходе. Обратите внимание, что arraySize = 232/rangeSize.

Нам нужно выбрать значение rangeSize так, чтобы памяти хватило и на первый (массив) и на второй (битовый вектор) проходы.

Первый проход: массив

Массив на первом проходе может вместить 10 Мбайт, или 223 байт, памяти. Поскольку каждый элемент в массиве относится к типу int, а переменная типа int занимает 4 байта, мы можем хранить примерно 221 элементов.

Второй проход: битовый вектор

Нижеприведенный код предоставляет одну реализацию для этого алгоритма:

			int bitsize = 1048576; // 2^20 bits (2^17 bytes)
int blockNum = 4096; // 2^12
byte[] bitfield = new byte[bitsize/8];
int[] blocks = new int[blockNum];

void findOpenNumber() throws FileNotFoundException {
	int starting = -1;
	Scanner in = new Scanner (new FileReader ("file.txt"));
	while (in.hasNextInt()) {
		int n = in.nextInt();
		blocks[n / (bitfield.length * 8)]++;
	}
	
	for (int i = 0; i < blocks.length; i++) {
		if (blocks[i] < bitfield.length * 8) {
			/* если значение < 2^20, то отсутствует как минимум 1 число
			 * в этой секции. */
			starting = i * bitfield.length * 8;
			break;
		}
	}
	
	in = new Scanner(new FileReader("input_file.txt"));
	while (in.hasNextInt()) {
		int n = in.nextInt();
		/* Если число внутри блока, в котором отсутствуют числа,
		 * мы записываем его */
		if (n >= starting && n < starting + bitfield.length * 8) {
			bitfield[(n - starting) / 8] |= 1 << ((n - starting) % 8);
		}
	}
	
	for (int i = 0 ; i < bitfield.length; i++) {
		for (int j = 0; j < 8; j++) {
			/* Получаем отдельные биты каждого байта. Когда бит 0
			 * найден, находим соответствующее значение. */
			if ((bitfield[i] & (1 << j)) == 0) {
				System.out.println(i * 8 + j + starting); return;
			}
		}
	}
}
		

А что если вам нужно решить задачу, используя более серьезные ограничения на использование памяти? В этом случае придется сделать несколько проходов. Сначала пройдитесь по «миллионным» блокам, потом по тысячным. Наконец, на третьем проходе можно будет использовать битовый вектор.

Разбор взят из перевода книги Г. Лакман Макдауэлл и предназначен исключительно для ознакомления.Если он вам понравился, то рекомендуем купить книгу «Карьера программиста. Как устроиться на работу в Google, Microsoft или другую ведущую IT-компанию».