Алгоритмическая задача про острова 

Ранее мы разбирали алгоритмическую задачу про острова в заданиях с собеседований для программистов. К существующему решению мы получили замечание от нашего пользователя и решили разобраться в сложности алгоритма подробнее.

Давайте проанализируем выбранный нами вариант и рассмотрим тот, который предложил пользователь Типичного Программиста.

1. Условие
2. Решение
3. Программный код
4. Проверяем решение
5. Сложность алгоритма
6. Решение от пользователя

Условие

Для двумерного массива M x N, состоящего из единиц, которые обозначают сушу, и нулей, обозначающих воду, верните количество островов.

Остров окружён водой и образован соединением соседних земель по горизонтали и вертикали. Вы можете предположить, что все четыре края матрицы окружены водой.

Примечание Если островов нет, возвращаем 0. Помечаем острова через 1, а воду обозначаем как 0.

Решение алгоритмической задачи про острова

Поиск в глубину — классический подход в решении подобных задач. Его суть заключается в том, что мы проходим по карте и для каждой 1 запускаем поиск в глубину, чтобы осмотреться вправо, влево, вверх и вниз. При каждом запуске поиска в глубину для корневого узла будем увеличивать счётчик с количеством островов.

Другими словами

Для начала нам нужно найти в матрице хотя бы одну единицу: начинаем построчный обход с нулевого индекса [0,0]. Когда мы находим единицу, помечаем её, как просмотренную, и также просматриваем соседние клетки по направлениям вправо, вниз, влево, вверх.

Если предыдущая ячейка была сушей, а следующая оказалась водой, мы возвращаемся к суше и просматриваем ячейки по перечисленным направлением в том же порядке.

Программный код

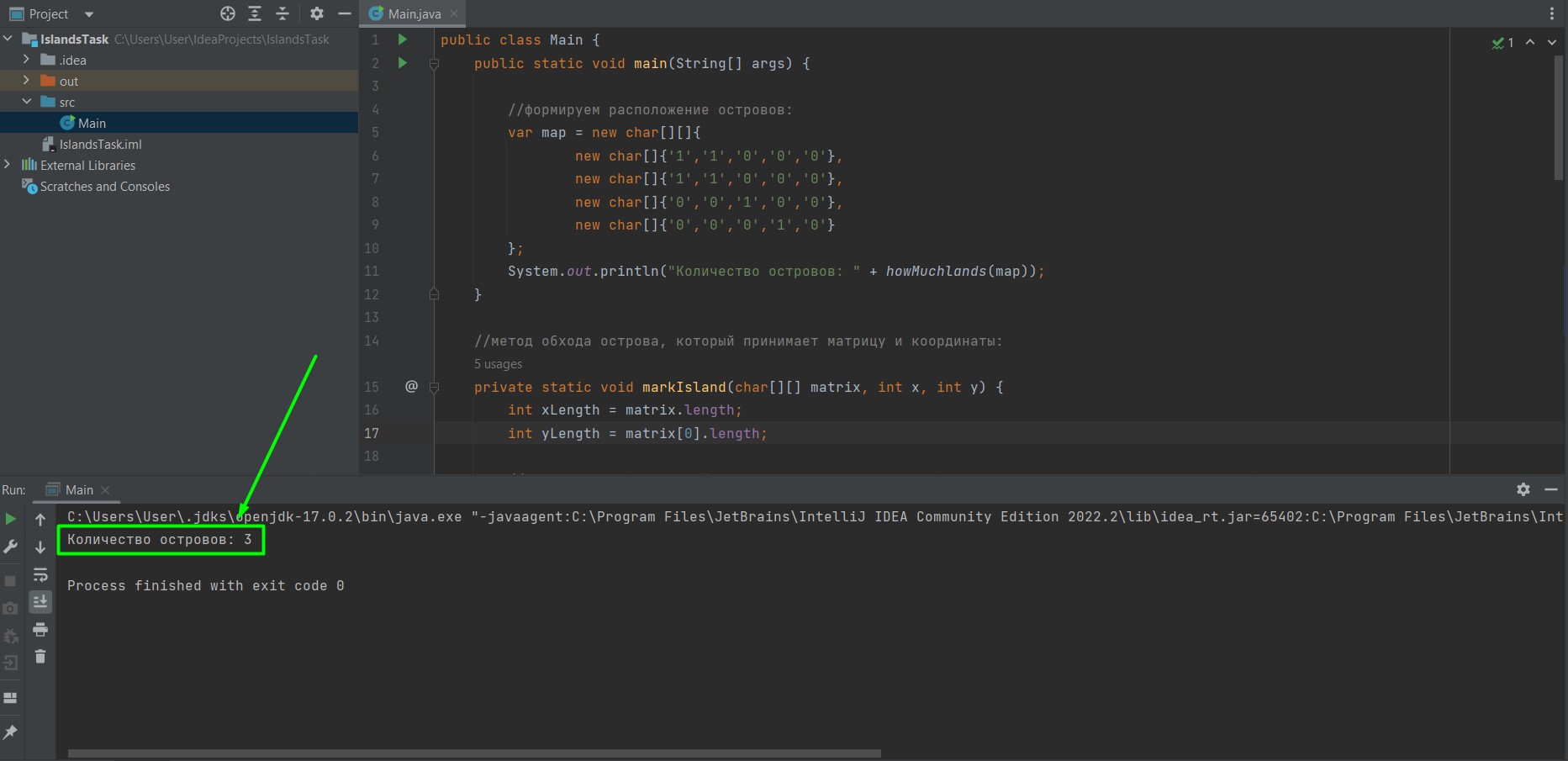
Напишем код на Java, используя три метода. Включая main, у нас также будет метод обхода острова, чтобы понять, что находится вокруг (есть ли там ещё земля или только вода), а также метод подсчёта островов, в котором и будет запускаться метод обхода.

Никаких дополнительных инструментов для реализации не нужно. В main пишем статичное расположение островов, но при желании можно поиграться с рандомной подстановкой 0 и 1.

			public class Main {
    public static void main(String[] args) {

        //формируем расположение островов:
        var map = new char[][]{
                new char[]{'1','1','0','0','0'},
                new char[]{'1','1','0','0','0'},
                new char[]{'0','0','1','0','0'},
                new char[]{'0','0','0','1','0'}
        };
        System.out.println("Количество островов: " + howMuchlands(map));
    }

    //метод обхода острова, который принимает матрицу и координаты:
    private static void markIsland(char[][] matrix, int x, int y) {
        int xLength = matrix.length;
        int yLength = matrix[0].length;

        //условие выхода за край матрицы:
        if (x < 0 || y < 0 || x >= xLength || y >= yLength || matrix[x][y] == '0') {
            return;
        }

        //если не вышли за границу, помечаем ячейку как 0:
        matrix[x][y] = '0';

        //осматриваемся:
        markIsland(matrix, x - 1, y); //вверх
        markIsland(matrix, x + 1, y); //вниз
        markIsland(matrix, x, y - 1); //влево
        markIsland(matrix, x, y + 1); //вправо
    }

    //метод расчёта:
    public static int howMuchlands(char[][] matrix) {
        int xLength = matrix.length;
        if (xLength == 0) return 0;
        int yLength = matrix[0].length;
        //переменная, хранящая кол-во островов:
        int numIslands = 0;

        //перебор строк:
        for (int i = 0; i < xLength; i++) {
            //перебор столбцов:
            for (int j = 0; j < yLength; j++) {
                if (matrix[i][j] == '1') {
                    //если находим "1", то увеличиваем каунтер островов:
                    numIslands++;
                    //запускаем метод обхода острова по периметру:
                    markIsland(matrix, i, j);
                }
            }
        }
        return numIslands;
    }
}
		

Проверяем решение

В случае с нашей картой и с учётом того, что по диагонали острова не соединяются, мы должны получить в результате три острова, что и видим на выходе программы:

Здесь вы можете запустить аналгичную программу на C#, а также изменить шаблон карты по своему усмотрению.

Сложность алгоритма

Сложность решения алгоритмической задачи про острова — O(m*n), где m — количество строк, а n — количество столбцов нашей матрицы.

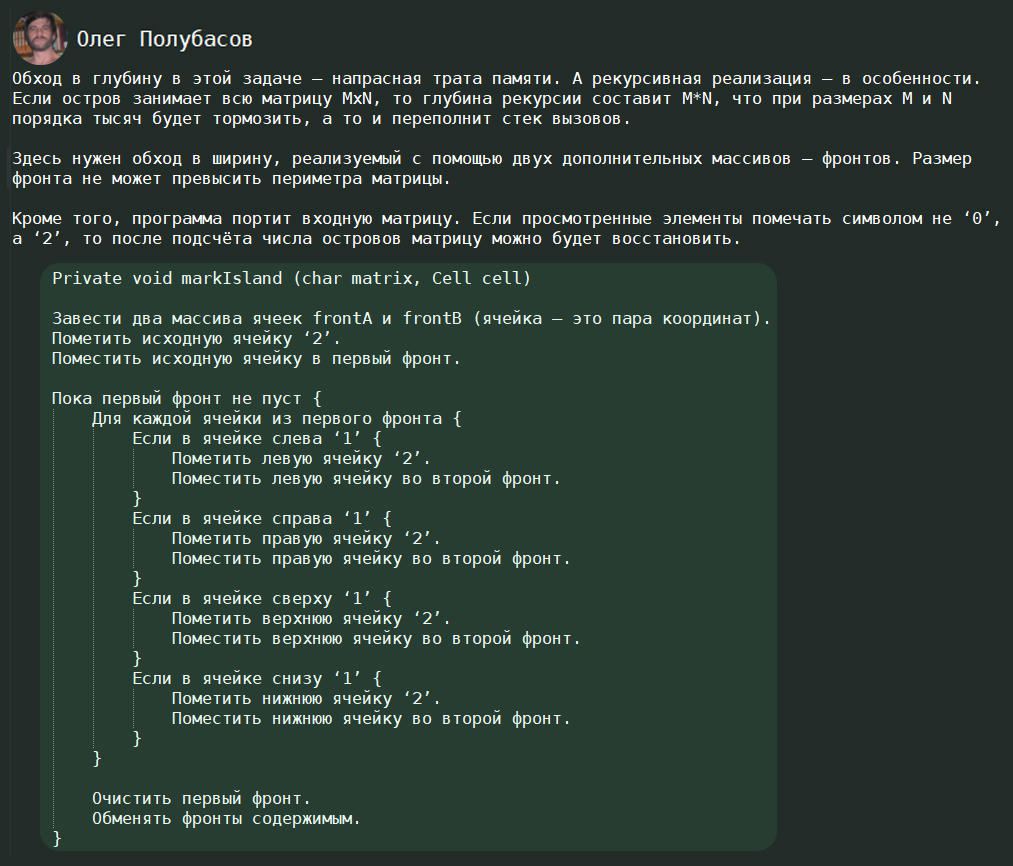
Решение от пользователя

Есть вариант более быстрого решения, при котором программа не затормозит в случае большого массива данных:

А с каким решением согласны вы? Может, у вас есть своё? Предложите альтернативную реализацию в комментариях.