Задача про вероятность попадания баскетбольного мяча в корзину

Вы должны выбрать одну из двух ставок. При первом варианте вы должны забросить баскетбольный мяч в корзину. Если попадёте, то получите 50 тыс. рублей. Во втором варианте вам надо попасть два раза из трёх бросков, и тогда вы также получите те же 50 тыс. рублей. Какой из этих вариантов вы предпочтёте?

Обозначим вероятность попадания в корзину р. При первом броске у вас шанс выигрыша 50 тыс. рублей равен р. В случае промаха вы ничего не получите. В среднем можно ожидать, что ваш выигрыш составит 50 000 × р.

При втором варианте вы бросаете три раза и должны попасть в корзину дважды, чтобы получить деньги. Вероятность попадания при каждой отдельной попытке по-прежнему составляет р. Вероятность промаха при любой попытке равна 1 – p.

При втором варианте имеется 23, или 8, сценариев развития. Давайте перечислим их в виде таблички. Знак ✓ означает, что вы попали, пустое место свидетельствует о том, что вы промахнулись.

Первый сценарий относится к ситуации, когда вы полностью провалили игру. Вы промазали при всех трёх бросках. Вероятность такого исхода составляет 1 – р, умноженная сама на себя три раза. Разумеется, при таком развитии событий никаких денег вы не получите.

В четырех из восьми сценариев вы выигрываете деньги. В трёх из них вы промахиваетесь один раз. У этих сценариев вероятность составляет p2(1 – p). В одном случае вы попадаете все три раза, вероятность чего равна p3. Сложите все эти вероятности. Три раза p2(1 – p) можно представить в виде 3p2 – 3p3. Добавьте к этой сумме p3, и вы получите 3p2 – 2p3. Ожидание составляет 50 000 × (3p2 – 2p3).

Какой из вариантов для вас лучше?

Ожидание при первом варианте: 50 000 × р.
Ожидание при втором варианте: 50 000 × (3p2 – 2p3).

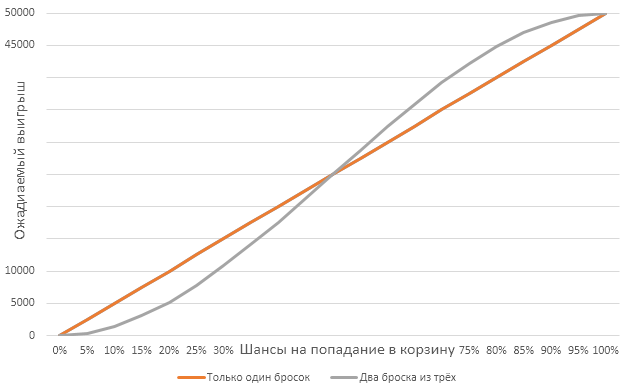
Вы можете быть полным профаном в баскетболе (р приблизительно равно 0) или мастером бросков, играющим в НБА. В качестве ссылки сделаем то, чего вы не сделаете на собеседовании, если вам дадут такую задачу: переведём формулу в электронную таблицу и составим график. Этот график показывает, как меняется ожидаемая величина выигрыша в зависимости от р.

Прямая диагональная линия отражает первый вариант ставки, S-образная кривая — второй. Первый вариант лучше для вас, если ваши шансы на попадание в корзину ниже 50%. В противном случае вам лучше выбрать второй вариант.

Это вполне объяснимо. Плохой игрок не может надеяться на победу ни при том, ни при другом варианте. Он должен рассчитывать лишь на слепую удачу, которая, очевидно, случится, скорее всего, один раз, а не дважды. Поэтому плохому игроку лучше выбрать первый вариант. Очень хороший игрок должен победить при любой ставке, хотя есть небольшая вероятность, что при единственном броске он промахнётся. Два из трех бросков лучше отражают степень его мастерства, и поэтому он захочет выбрать этот вариант. Существует юридическое правило: если вы виноваты, вы хотите, чтобы ваше дело рассматривал суд присяжных (потому что всё может случиться); если невиновны, для вас лучше, чтобы ваше дело рассматривал один судья.

Если вы дошли в своих рассуждениях до этого момента, то интервьюер на собеседовании задаст вам следующий вопрос: какое значение р заставит вас перейти от одного варианта к другому? Чтобы ответить на этот вопрос, приравняйте вероятности выигрыша в обеих ставках. Вы получите уровень мастерства, при котором выбор ставки можно сделать путем подбрасывания монеты.

p = 3p2 – 2p3

Разделите обе части уравнения на p:

1 = 3p – 2p2,

и тогда вы получите

2p2 – 3p + 1 = 0.

Добравшись до этого места, вы можете просто решить это квадратное уравнение, мысленно поблагодарив своего школьного учителя математики. Интервьювер отметит не только знание вами материала учебника, но и то, как живо вы выполните эти вычисления. Вы знаете, что р — вероятность — должна быть между 0 и 1. Лучше всего попробовать разумное значение: «Хорошо, мне необходимо число от 0 до 1. Давайте попробуем 0.5». Такой ответ сработает.

Разбор по книге «Are You Smart Enough to Work at Google?».