Подборка задачек: считаем спички, капли и вычисляем лживых осьминогов
Предлагаем вам немного отдохнуть от рутины и порешать увлекательные логические задачки про спички, капли и приключения короля осьминогов.
Игра со спичками
N спичечных кучек с различным количеством спичек расположены в ряд (предположим, что кучек четное количество). Два игрока по очереди забирают себе по крайней куче, пока не останется ни одной. Игрок с большим количество спичек побеждает.
Вы бы предпочли ходить первым или вторым? Это имеет значение?
Предположим, что вы ходите первым — предложите алгоритм для получения максимального количества спичек, которое вы сможете выиграть.
Стратегия, просто основанная на заборе максимальной из 2-х крайних куч, может не работать. В следующем примере первый игрок проигрывает, если забирает максимальную из 2-х куч каждый ход:
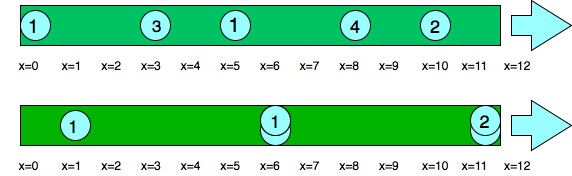
Расстановка 18 20 15 30 10 14:
- Первый игрок забирает 18, осталось: 20 15 30 10 14.
- Второй игрок забирает 20, осталось: 15 30 10 14.
- Первый игрок забирает 15, осталось: 30 10 14.
- Второй игрок забирает 30, осталось: 10 14.
- Первый игрок забирает 14, осталось: 10.
- Второй игрок забирает 10, конец игры.
Второй игрок (20+30+10) собрал в итоге больше, чем первый (18+15+14) и выиграл.
Line matchsticks game
There are n piles with different number of matchsticks in a line. (Assume n is even). Two players take turns to take a pile from one of the ends of the line until there are no more piles left. The player with the larger amount of matches wins.
Would you rather go first or second? Does it matter?
Assume that you go first, describe an algorithm to compute the maximum amount of matches you can win.
Note that the strategy to pick maximum of two corners may not work. In the following example, first player loses the game when he/she uses strategy to pick maximum of two corners.
Example 18 20 15 30 10 14
- First Player picks 18, now row of matches is 20 15 30 10 14
- Second player picks 20, now row of matches is 15 30 10 14
- First Player picks 15, now row of matches is 30 10 14
- Second player picks 30, now row of matches is 10 14
- First Player picks 14, now row of matches is 10
- Second player picks 10, game over.
The total value collected by second player is more (20 + 30 + 10) compared to first player (18 + 15 + 14). So the second player wins.
Возможность походить первым означает, что Вы не проиграете. Используя следующую стратегию, Вы будете всегда выигрывать или, как минимум, заканчивать ничьей.
- Посчитайте сумму всех нечетных кучек (пусть будет X).
- Посчитайте сумму всех четных кучек (пусть будет Y).
- Если X > Y, начинайте с левой кучки. Всегда выбирайте нечетные кучки в свой ход.
- Если X < Y, начинайте с правой и выбирайте четные кучки.
- Если X = Y, вы гарантируете ничью в случае, если будете брать только четные или нечетные кучки.
Что означает «выбирать всегда четные/нечетные» кучки? Посмотрим на следующем примере шести кучек:
18 20 15 30 10 14
Сумма нечетных = 18+15+10 = 43
Сумма четных = 20 + 30 + 14 = 64.
Поскольку сумма четных больше, первый игрок решает собрать все четные кучки. Он забирает 14, так что второй игрок может взять только 10 или 18. Чтобы он ни выбрал у первого игрока всегда будет возможность четную кучку и заблокировать доступ к четным кучкам для второго игрока.
Going first will guarantee that you will not lose. By following the strategy below, you will always win the game (or get a possible tie).
- Count the sum of all matches that are odd-numbered. (Call this X)
- Count the sum of all matches that are even-numbered. (Call this Y)
- If X > Y, take the left-most pile first. Choose all odd-numbered piles in subsequent moves.
- If X < Y, take the right-most pile first. Choose all even-numbered piles in subsequent moves.
- If X == Y, you will guarantee to get a tie if you stick with taking only even-numbered/odd-numbered piles.
You might be wondering how you can always choose odd-numbered/even-numbered piles. Look at the illustration using an example where you have 6 piles:
Example:
18 20 15 30 10 14
Sum of odd piles= 18 + 15 + 10 = 43
Sum of even piles = 20 + 30 + 14 = 64.
Since the sum of even match piles is more, the first player decides to collect all even coins. He first picks 14, now the other player can only pick a pile (10 or 18). Whichever is picked the other player, the first player again gets an opportunity to pick an even pile and block all even piles.
Капли в трубе
Рассмотрим трубу длиной L. В трубе присутствует N капель на N различных позициях. Каждая капля движется к концу трубы (x = L) с разной скоростью. Когда капля смешивается с другой каплей, она принимает скорость капли с которой смешивается. Напишите программу для определения количества капель, которые вытекут из трубы.
См. рисунок ниже:
Пример:
Вход: длина = 12, позиции = [10,8, 0, 5, 3], скорость = [2, 4, 1, 1, 3].
Выход: 3.
Объяснение:
Капли, начинающие с позиций x=10 и x=8 станут одной каплей, встретившись в х=12 через одну секунду. Капля, начинающие с позиции 0 ни с кем не смешается, поэтому выйдет как есть. Капли, начинающие с позиций x=5 и x=3 объединятся в одну каплю на позиции х=6 во время равное t=1 сек. Никакие другие капли им не встретятся до конца трубы, поэтому ответом к задаче будет 3. Рассмотрим иллюстрацию.
Цифры на каплях означают скорость:
Droplets in the pipe
Consider a pipe of length L. The pipe has N water droplets at N different positions within it. Each water droplet is moving towards the end of the pipe (x=L) at different rates. When a water droplet mixes with another water droplet, it assumes the speed of the water droplet it is mixing with. Write a program to determine the no of droplets that come out of the end of the pipe.
Refer to the figure below:
Examples:
Input: length = 12, position = [10, 8, 0, 5, 3], speed = [2, 4, 1, 1, 3].
Output: 3.
Explanation:
Droplets starting at x=10 and x=8 become a droplet, meeting each other at x=12 at t=1 sec. The droplet starting at 0 doesn’t mix with any other droplet, so it is a drop by itself. Droplets starting at x=5 and x=3 become a single drop, mixing with each other at x=6 at t=1 sec. Note that no other droplets meet these drops before the end of the pipe, so the answer is 3.
Refer to the figure below. Numbers on circles indicates speed of water droplets.
При решении этой задачи используется жадная техника. Капля смешивается с другой каплей, только если выполняются два условия:
- Если капля быстрее той, с которой она смешивается.
- Если позиция быстрой капли находится за позицией медленной капли.
Используем массив для хранения пар значений — позиции и времени, нужного для достижения конца трубы. Отсортируем массив по позиции. Теперь у нас есть понимание, какие капли расположены за какими и их время для достижения конца трубы. Большее время означает меньшую скорость и меньшее время означает большую скорость. Все капли, находящиеся сзади медленных капель смешиваются с ними. А все капли находящиеся перед медленными каплями смешиваются со следующими медленными каплями и т.д. Например, время до конца трубы будет — 12, 3, 7, 8, 1 (отсортировано по позиции).
- Нулевая (индекс в массиве) капля — самая медленная и не смешается со следующей каплей.
- Первая капля быстрее второй, следовательно, они смешаются.
- Вторая капля быстрее чем третья и все три сольются. Они не смешаются с четвёртой, которая быстрее.
Используем стек для хранения локальных максимумов времени. Количество локальных максимумов + остаток (капли, после последнего максимума) = общее количество вытекших капель.
This problem uses greedy technique. A drop will mix with another drop if two conditions are met:
- If the drop is faster than the drop it is mixing with.
- If the position of the faster drop is behind the slower drop.
We use an array of pairs to store the position and the time that ith drop would take to reach the end of the pipe. Then we sort the array according to the position of the drops. Now we have a fair idea of which drops lie behind which drops and their respective time taken to reach the end.More time means less speed and less time means more speed. Now all the drops before a slower drop will mix with it. And all the drops after the slower drop with mix with the next slower drop and so on.
For example if the times to reach the end are- 12, 3, 7, 8, 1 (sorted according to positions).
0th drop is slowest, it won’t mix with the next drop, 1st drop is faster than the 2nd drop so they will mix and 2nd drop is faster than 3rd drop so all three will mix together. They cannot mix with the 4th drop because that is faster.
So we use a stack to maintain the local maxima of the times.
No of local maximal + residue(drops after last local maxima) = total no of drops.
Король Осьминог
У короля Осминога есть слуги с шестью, семью и восемью ногами. Слуги с семью ногами всегда лгут, но слуги с 6 или 8 ногами всегда говорят правду.
Однажды встретились 4 слуги:
- Синий заметил: «Всего у нас 28 ног»;
- Зеленый ответил: «У нас 27 ног»;
- Желтый сказал: «У нас 26 ног»;
- А красный заметил: «У нас 25 ног»;
Слуга какого цвета сказал правду?
King Octopus
King Octopus has servants with six, seven, or eight legs. The servants with seven legs always lie, but the servants with either six or eight legs always say the truth.
One day, 4 servants met :
- The blue one says: “Altogether we have 28 legs”;
- the green one says: “Altogether we have 27 legs”;
- the yellow one says: “Altogether we have 26 legs”;
- the red one says: “Altogether we have 25 legs”.
What is the colour of the servant that says the truth?
Зеленый слуга сказал правду.
Будем предполагать, что один из слуг сказал правду и попробуем доказать это. Поскольку трое несогласны, следовательно, 3 всегда врут.
Предположим, что прав был синий, тогда у синего 6 или 8 ног. А у каждого из остальных по семь ног, поскольку лживые слуги имеют 7 ног. Следовательно, суммарное количество ног должно быть 6 + 7 + 7 + 7 = 27 или 8 + 7 + 7 + 7 = 29. Но поскольку синий сказал, что ног 28, следовательно он лжет. Если мы применим такую же логику для остальных высказываний, мы убедимся, что правду о количество ног сказал только зеленый слуга.
The green one is telling the truth.
Lets assume that one of them is telling the truth and then try to prove that. Since the four are disagreeing then 3 must be lying.
Lets say blue is telling the truth: so the blue one has either 6 or 8 legs. And each of the other octopus is lying hence has 7 legs. So our total legs becomes: 6 + 7 + 7 + 7 = 27 legs or 8 + 7 + 7 + 7 = 29 legs. But since blue said altogether we have 28 legs, we know he is lying.
If you follow this same logic for all of them, you realize that only the Green octopus can be telling the truth as the number of legs adds up.