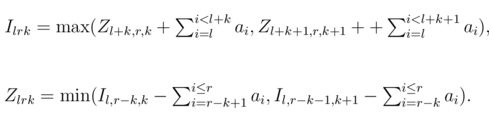14 алгоритмических задач с разбором решений — итоги «Технокубка» 2017

Технокубок — это олимпиада по программированию, организованная Mail.Ru Group, МГТУ им. Н. Э. Баумана и МФТИ для учеников 8-11 классов, а также потенциальная возможность попасть в лучшие технические вузы благодаря успехам в программировании.

Позади два отборочных тура Технокубка 2016/2017, 25 декабря прошел и третий отборочный раунд. Теперь ожидается главное событие — очное состязание в марте 2017. До него еще несколько месяцев, можно проштудировать пару ресурсов или заглянуть в группу чемпионата Вконтакте. Кроме того, полезно будет посмотреть разбор задач прошедших отборочных раундов (приведен ниже).

Первый “Пилотный” Технокубок был организован в крайне сжатые сроки. С момента возникновения идеи (а ее, к слову, подал один из студентов МГТУ им. Н. Э. Баумана) до презентации проекта руководству прошел всего месяц. В заочных этапах школьникам предлагалось решить пять задач, по результатам которых 150 участников каждого отборочного тура приглашались в финал. Во время очного этапа в течение трех часов участники решали задачи на площадках МГТУ им. Н. Э. Баумана и МФТИ. Все происходило в режиме онлайн. Ребята соревновались в написании кода и “взламывании” чужих задач — по словам участников, это было азартно и увлекательно. Codeforces и преподаватели вузов, которые разрабатывали задания, старались сделать их максимально интересными.

Технокубок сегодня — это 5500 пользователей, 1000 участников в каждом отборочном раунде, 200 лучших, уже прошедших в финал. В ходе олимпиады участникам предлагается решать алгоритмические задачи и придумывать тесты для решений своих коллег. Если ты не увлечен программированием, справиться с заданиями Технокубка невозможно. Участники чемпионата – ребята, которые целенаправленно собираются поступать в ведущие технические вузы.

С 2017 года победа и призерство в чемпионате дают официальные льготы при поступлении в российские вузы. Партнер Технокубка, МФТИ, предлагает победителям 100 баллов по информатике. А поступление в МГТУ им. Н. Э. Баумана для победителей чемпионата возможно вовсе без вступительных испытаний.

И напоследок — обещанный разбор задач первого и второго отборочных раундов.

Разбор задач первого отборочного раунда

727A — Превращение: из A в B

У Василия есть число a, которое он хочет превратить в число b. Для этого он может производить два типа операций:

• умножить имеющееся у него число на 2 (то есть заменить число x числом 2·x);
• приписать к имеющемуся у него числу цифру 1 справа (то есть заменить число x числом 10·x + 1).

Вам надо помочь Василию получить из числа a число b с помощью описанных операций, либо сообщить, что это невозможно.

Обратите внимание, что в этой задаче не требуется минимизировать количество операций. Достаточно найти любой из способов получить из числа a число b.

Разбор решения

Будем решать задачу в обратную сторону — попытаемся получить из числа B число A.

Заметим, что если число B заканчивается на 1, то последняя операция, которую использовал Василий — приписать к числу справа 1. Поэтому удалим последнюю цифру из B и перейдем к новому числу.
Если же последняя цифра четная, то последняя операция, которую использовал Василий — умножить число на 2. Поэтому поделим B пополам и перейдем к новому числу.
Если же B заканчивается на нечетную цифру, отличную от 1, то ответ — “NO”.
После того как мы перешли к новому числу, нужно вновь выполнить описанный алгоритм. Если на каком-то шаге мы получили число, равное A, то мы нашли ответ, а если же мы получили число, меньшее A, то ответ “NO”.

727B — Сумма чека

Василий вышел из магазина, и ему стало интересно пересчитать сумму в чеке. Чек представляет собой строку, в которой названия покупок и их цены записаны подряд без пробелов. Чек имеет вид «name1price1name2price2…namenpricen», где namei (название i-го продукта) — это непустая строка длины не более 10, состоящая из строчных букв латинского алфавита, а pricei (цена i-го продукта) — это непустая строка, состоящая из точек и цифр. Продукты с одинаковым названием могут иметь разные цены.

Цена каждого продукта записана в следующем формате. Если продукт стоит целое количество рублей, то копейки не пишутся.

Иначе, после записи количества рублей к цене приписывается точка, за которой следом ровно двумя цифрами записаны копейки (если копеек менее 10, то используется лидирующий ноль).

Также, каждые три разряда (от менее значимых к более значимым) в записи рублей разделяются точками. Лишние лидирующие нули недопустимы, запись цены всегда начинается с цифры и заканчивается цифрой.

Например, записи цен:

• «234», «1.544», «149.431.10», «0.99» и «123.05» являются корректными,
• «.333», «3.33.11», «12.00», «.33», «0.1234» и «1.2» не являются корректными.

Напишите программу, которая по содержимому чека найдет суммарную цену всех покупок.

Разбор решения

В данной задаче нужно было аккуратно сделать то, что написано в условии. Можно было сначала выделить все последовательности из подряд идущих цифр и точек, которые являлись ценами.

Затем нужно было выделить целое количество рублей из каждой цены и отдельно считать сумму всех целых цен в переменную r. То же нужно было делать для копеек из каждой цены и складывать их в переменную c.

После обработки всех цен нужно было перевести копейки в рубли, то есть прибавить к r величину c / 100 (целая часть от деления c на 100), а c присвоить значению c%100 (остаток от деления c на 100). После этого осталось только аккуратно вывести ответ, не забыв, что если c < 10, то сначала для копеек нужно вывести 0, а затем c, так как количество копеек по условию обязательно должно состоять из двух цифр.

727C — Восстановления массива

Это интерактивная задача. Вам нужно использовать операцию flush после вывода каждого запроса. Например, в C++ вы должны использовать функцию fflush(stdout), в Java — использовать System.out.flush(), а в Паскале — flush(output).

В этой задаче вам надо восстановить массив, который заранее вам неизвестен. Вы можете считать, что жюри загадало некоторый массив a, про который вам известна только его длина n.

Единственное допустимое действие — узнать сумму пары элементов, указав их индексы i и j (индексы должны быть различными). В результате запроса для индексов i и j вы получите сумму ai + aj.

Известно, что восстановить весь загаданный массив можно не более чем за n запросов. Напишите программу, которая восстановит загаданный жюри массив a длины n за не более чем n запросов на сумму двух элементов (в каждом запросе индексы двух элементов должны быть различны).

Протокол взаимодействия

Каждый тест в этой задаче состоит из одного массива, который ваша программа должна восстановить.

В первой строке входных данных следует целое положительное число n (3 ≤ n ≤ 5000) — длина загаданного массива. В первую очередь ваша программа должна прочитать это число.

Далее ваша программа должна выводить в стандартный вывод запросы на сумму двух элементов массива, либо сообщить о том, что загаданный жюри массив уже найден.

В случае, если программа осуществляет запрос на сумму, то следует вывести строку вида «? i j» (i и j — различные целые числа от 1 до n) — индексы элементов массива, сумму которых ваша программа запрашивает.

В случае, если программа сообщает восстановленный массив, то следует вывести строку вида «! a1 a2 … an» (гарантируется, что все ai в правильно восстановленном массиве — положительные целые числа и не превосходят 105), где ai равно числу, стоящему в массиве в позиции i.
Результатом запроса на сравнение является единственное целое число, равное ai + aj.

Для массива длины n ваша программа должна сделать не более n запросов на сумму. Обратите внимание, что вывод строки вида «! a1 a2 … an» не считается запросом и не учитывается при подсчете их количества.

Не забывайте использовать операцию flush после каждой выведенной строки.

После вывода ответа ваша программа должна завершиться.

Разбор решения

Изначально сделаем три запроса на сумму чисел a1 + a2 = c1, a1 + a3 = с2 и a2 + a3 = c3.

После этого мы получаем систему из трех уравнений с тремя неизвестными a1, a2, a3. После простых вычислений получим, что a3 = (c3 - c1 + c2) / 2. После этого легко находятся a1 и a2. Теперь мы знаем значения a1, a2, a3, потратив на это 3 запроса.

Затем для всех i от 4 до n нужно сделать запрос на сумму a1 + ai. Если очередная сумма равна ci, то ai = ci - a1 (напомним, что мы уже знаем значение a1).

Таким образом можно восстановить весь массив, потратив на это ровно n запросов.

727D — Распределение футболок

В качестве сувениров на соревновании по программированию было решено вручить футболки. Всего в типографии были напечатаны футболки шести размеров: S, M, L, XL, XXL, XXXL (размеры перечислены в порядке возрастания). Для каждого размера от S до XXXL вам известно количество футболок такого размера.

Во время регистрации организаторы попросили каждого из n участников указать размер футболки. Если участник колебался между двумя размерами, то он мог указать два соседних — это означает, что ему подойдет футболка любого из двух размеров.

Напишите программу, которая определит, возможно ли из напечатанных в типографии футболок сделать подарок каждому участнику соревнования. Конечно, каждому участнику должна достаться футболка его размера:

• требуемого размера, если указан один размер;
• любого из двух размеров, если указаны два соседних размера.

В случае положительного ответа программа должна найти любой из вариантов раздачи футболок.

Разбор решения

Пусть в массиве cnt хранится, сколько в типографии есть футболок каждого из размеров.

Изначально раздадим футболки тем, кто точно хочет футболку одного размера, уменьшая при этом соответствующее значение в массиве cnt. Если в какой-то момент футболки не хватило, то ответа не существует.

Теперь осталось раздать футболки тем, кто хочет футболку одного из двух размеров. Поступим жадным образом. Раздадим по максимуму футболки размера S тем, кто хочет их или футболки размера M.

После этого перейдем к футболкам размера M и сначала раздадим их по максимуму тем, кто хочет футболки размера S или M, но кому не хватило футболок S, а затем, если остались футболки размера M, раздадим их тем, кто хочет их или футболки размера L. Аналогичным образом раздадим футболки оставшихся размеров.

Если после всех операций с футболками у кого-то футболки не оказалось, значит ответа не существует, в противном случае, ответ найден.

727E — Игры на диске

У Толи было n компьютерных игр, и он решил записать их на один диск. После этого он решил написать маркером названия всех своих игр на этом диске по кругу по часовой стрелке друг за другом. Названия всех игр были различные, а длина каждого названия была ровно k. Написанные названия на диске не перекрываются между собой.

После того, как Толя написал названия всех игр, на диске получилась циклическая строка длины n·k.

Прошло несколько лет и Толя уже и забыл, какие игры записаны на его диске. Он помнит, что всего в то время было g популярных игр, и на его диске могут быть только лишь эти игры, причем каждая из g игр может быть записана на диске не более одного раза.

Перед вами стоит задача восстановить любой корректный список игр, которые Толя мог записать на свой диск.

Разбор решения

С помощью алгоритма Ахо-Корасика построим суффиксное дерево на множестве названий игр так, что в вершине дерева, соответствующей названию некоторой игры, (вершине на глубине k) будем хранить номер этой игры.

Построенный бор позволяет приписывать к некоторой строке символы один за другим и определять вершину в нем, соответствующую наидлиннейшему префиксу из всех префиксов названий игр, совпадающему с суффиксом нашей строки. Если длина этого префикса равна k, то суффикс совпадает с некоторым названием игры.

Запишем строку из входных данных дважды и посчитаем idxi — индекс игры, название которой совпадает с подстрокой удвоенной строки с индекса i - k + 1 по индекс i включительно (если такой нет, то -1).

Теперь остается перебрать индекс символа, который является последним в записи названия некоторой игры на диск. Очевидно, этот индекс можно перебирать от 0 до k - 1. С фиксированным индексом f достаточно проверить, что все названия с последними символами в индексах f + ik mod nk для 0 ≤ i < n являются различными (для этого смотрим, что среди idx(f + ik)%nk + nk нет -1 и все они различны). Если это выполняется — выводим YES и легко восстанавливаем ответ. Если ни для одного f условия не выполнились, выводим NO.

Асимптотика решения — O(nk + ∑|ti|)

727F — Задачи Поликарпа

Поликарп — опытный участник соревнований по программированию Codehorses. Теперь он решил попробовать себя в качестве автора задач.

Он отослал координатору раундов набор из n задач. Каждая задача характеризуется своим качеством, качество i-й задачи равно ai (ai может быть положительно, отрицательно или равно нулю). Задачи отсортированы по предполагаемой сложности, которая никак не связана с качеством. Таким образом, самая простая задача имеет номер 1, а самая сложная — номер n.

В настоящий момент настроение координатора равно q. Известно, что после чтения очередной задачи его настроение изменяется на качество этой задачи, то есть после того, как координатор прочитает задачу с качеством b, к его настроению добавляется величина b. Координатор всегда читает задачи подряд от самой простой к самой сложной, порядок чтения задач изменять нельзя.

Если в какой-то момент текущее настроение координатора становится отрицательным, то он немедленно прекращает чтение и полностью отклоняет весь комплект задач.

Поликарп хочет выбросить минимальное количество задач так, чтобы настроение координатора всегда было неотрицательным. Так как Поликарп не знает точно текущее настроения координатора, то у него есть m гипотез вида «текущее настроение координатора q = bi».

Для каждой из m гипотез найдите минимальное количество задач, которое надо удалить из комплекта, чтобы при чтении оставшихся задач от самой простой к самой сложной настроение координатора всегда было больше или равно 0.

Разбор решения

Для начала решим задачу для одного значения Q. Нетрудно показать, что оптимальным поведением является следующее: добавляем в множество оставленных задач очередную задачу качества ai; пока значение настроения (сумма качеств и Q) является отрицательным, удаляем из множества оставленных задач задачу с наихудшим качеством. Качество такой задачи обязательно будет отрицательным, поэтому мы не испортим значения настроения на предыдущих задач. Такое моделирование просто осуществляется с помощью структур std::set или std::priority_queue.

Соображение выше позволяет нам отвечать на запрос за O(n log n), однако O(mn log n) не укладывается в ограничение по времени. Поэтому нужно заметить, что при увеличении Q количество удаленных задач не увеличивается, а возможных таких количеств всего n. Таким образом, на задачу нужно взглянуть с обратной стороны: для 0 ≤ x ≤ n посчитать, какое наименьшее значение может иметь Q так, что количество удаленных задач не превосходит x. Эта задача просто решается для каждого x с помощью бинпоиска за O(n log n log MAXQ), в сумме по всем x получим O(n2 log n log M AXQ). Если еще и учесть, что нас интересуют только m значений Q, то бинпоиск осуществлять можно только по ним и получить O(n2 log n log m)

По сохраненным значениям для каждого ответа x остается только найти первый ответ, наименьшее значение Q для которого не больше значения Q в запросе. Это можно делать наивно за O(n) или же с помощью бинарного поиска за O(log n) (значения Q для ответов не возрастают), получая O(mn) или O(m log n) в сумме.
Наилучшая асимптотика составит O(n2 log n log m + m log n), однако решения за O(n2 log n log MAXQ + mn) тоже проходят все тесты.

Разбор задач второго отборочного раунда

729A — Интервью с Олегом

Поликарп взял у Олега интервью и записал его себе в блокнот без знаков препинания и пробелов, чтобы сэкономить время и успеть все записать. В итоге, интервью представляет собой строку s, состоящую из n строчных букв латинского алфавита.

В речи Олега есть слово-паразит ogo, а также все слова, которые получаются из слова ogo приписыванием справа к нему слога go. Например, слова ogo, ogogo, ogogogo являются паразитами, а слова go, og, ogog, ogogog и oggo — не являются.

Слова-паразиты имеют максимальный возможный размер, то есть, например, в речи ogogoo нельзя считать, что слово-паразит это ogo, а goo является частью обыкновенной фразы интервью. В данном случае словом-паразитом является подстрока ogogo.

До печати Поликарпу необходимо заменить каждое слово-паразит на последовательность из трёх звездочек. Обратите внимание, что независимо от длины слова-паразита оно заменяется ровно на три звёздочки.

Поликарп быстро справился с этой задачей. А сможете ли это сделать вы? Время пошло!

Разбор решения

В этой задаче достаточно идти по строке слева направо и из каждого очередного индекса искать наидлиннейшую подстроку вида “ogo…go”. Если такая найдена, то к ответу надо дописать “***” и перейти за ее конец, иначе надо дописать к ответу очередную букву и перейти к следующей позиции.

729B — Прожекторы

Театральная сцена представляет собой прямоугольное поле размером n × m. Директор театра выдал вам план сцены, согласно которому на ней будут располагаться актёры. На плане отмечено в каких клетках будут стоять актёры, а в каких нет.

Прожектор, установленный на сцену, будет светить в одном из четырёх направлений (если смотреть на план сцены сверху) — влево, вверх, вправо или вниз. Таким образом, под позицией прожектора понимается клетка, в которую он установлен, а также направление, в котором он светит.

Перед вами стоит задача поставить на сцену прожектор в хорошую позицию. Позиция называется хорошей, если одновременно выполняются два условия:

• в соответствующей ей клетке нет актёра;
• в направлении, в котором светит прожектор, находится хотя бы один актёр.

Перед вами стоит задача посчитать количество хороших позиций для установки прожектора. Две позиции установки прожектора считаются различными, если отличаются клетки расположения прожектора, или направление, в котором он светит.

Найдем количество хороших позиций, где прожектор направлен влево. Это можно сделать отдельно по каждой строке. Для этого надо сканировать строку слева направо, поддерживая флаг, что была встречена ‘1’ (например, в переменной f). Тогда при обработке очередного значения:

• если оно равно ‘0’, то к ответу следует прибавить единицу, если f равен true;
• если оно равно ‘1’, то f := true.

Аналогично можно посчитать количество позиций для других трех направлений.

729C — Дорога до кинотеатра

Вася находится в центре проката машин и хочет как можно скорее добраться до кинотеатра. Сеанс, на который он уже купил билет, начнётся через t минут. Считайте, что есть прямая дорога от центра проката машин до кинотеатра длиной s километров. Введём систему координат так, что центр проката машин находится в точке 0, а кинотеатр находится в точке s.

Известно, что по пути от центра проката машин до кинотеатра есть k заправочных станций, причём на всех можно заливать неограниченное количество топлива совершенно бесплатно! Считайте, что операция залива топлива осуществляется мгновенно.

В центре проката есть n машин, i-я из которых характеризуется двумя числами ci и vi — стоимостью аренды машины и вместимостью её бака. Таким образом, на заправке нельзя заливать в машину топлива больше вместимости её бака vi. В центре проката все машины изначально полностью заправлены.

Каждая из машин может ехать в одном из двух скоростных режимов: обычном и ускоренном. В обычном режиме машина проезжает 1 километр за 2 минуты, при этом тратит на это 1 литр топлива. В ускоренном режиме машина проезжает 1 километр за 1 минуту, при этом тратит на это 2 литра топлива. Режим может быть изменён в любой момент. Изменять режим разрешается неограниченное количество раз.

Перед вами стоит задача выбрать машину с минимальной стоимостью аренды, на которой Вася успеет добраться до кинотеатра до начала своего сеанса, то есть не позднее, чем через t минут. Считайте, что в центре проката все машины изначально полностью заправлены.

Разбор решения

Понятно, что существует такое значение размера бака (назовем его w), что если машина имеет бак равный или больший w, то она доедет до кинотеатра вовремя, иначе — не успеет.

Значение w можно найти бинарным поиском, ведь функция can(w) (сможет ли и успеет ли доехать машина) является монотонной — она сначала имеет значения false, затем true.

После нахождения w достаточно среди всех машин с размером бака w или более выбрать наиболее дешевую.

Функцию can(w) можно реализовать, жадно моделируя процесс. Легко написать формулу для нахождения количества километров, которые можно проехать в режиме ускорения, если ближайшая заправка находится на расстоянии x, а сейчас у нас f литров бензина:

• если x > f, то доехать вообще нельзя и функция can(w) должна вернуть false,
• если x ≤ f, то в режиме ускорения проехать можно min(x, f - x) километров.

Таким образом, за один проход по массиву заправок в порядке возрастания их отдаления можно посчитать значение can(w).

729D — Морской бой

Галя играет в одномерный морской бой на поле размера 1 × n. В этой игре на клеточном поле расположены a кораблей, каждый состоит из b последовательных клеток. При этом одна клетка не может являться частью более чем одного корабля, однако, корабли могут соприкасаться.

Гале неизвестно положение кораблей. Галя может делать выстрелы по клеткам, при этом после каждого выстрела ей сообщается, является эта клетка частью какого-нибудь корабля (в таком случае считается, что Галя «попала»), или нет (тогда Галя «промахнулась»).

Галя уже сделала k выстрелов и все из них были промахами.

Перед вами стоит задача определить минимальное количество позиций, выстрелив в которые, Галя гарантированно попадет хотя бы в один из кораблей.

Гарантируется, что существует хотя бы одна расстановка кораблей, удовлетворяющая описанным условиям.

Разбор решения

Заметим факт, что если на поле есть b подряд идущих нулей, то обязательно надо выстрелить в один из них. Предположим, что все корабли были максимально прижаты вправо. Поставим двойки в те клетки, где могут находиться максимально прижатые вправо корабли. Проитерируемся по клеткам поля, начиная слева, и будем стрелять в клетку, если в ней стоит 0 и до этого был b - 1 подряд идущий ноль. После этого останется выстрелить в одну любую клетку, в которой стоит двойка. Все описанные выстрелы и будут ответом.

729E — Подчиненные

В крупной компании работают n сотрудников, каждый из которых имеет уникальный номер от 1 до n. Из них ровно один сотрудник является главным, его номер равен s. Также известно, что все сотрудники, кроме главного, имеют ровно одного непосредственного начальника.

Каждому из сотрудников было поручено подать информацию о том, сколько начальников у него есть (не только непосредственных). Под начальниками сотрудника понимается его непосредственный начальник, а также непосредственный начальник непосредственного начальника данного сотрудника, и так далее. Например, если в компании три сотрудника, первый из которых главный, у второго сотрудника непосредственный начальник — первый сотрудник, а у третьего сотрудника непосредственный начальник второй сотрудник, то у третьего сотрудника всего два начальника — один непосредственный и один не непосредственный. Главный сотрудник является начальником всех сотрудников, кроме самого себя.

Некоторые из сотрудников поторопились, ошиблись в подсчете и подали неверную информацию. Перед вами стоит задача определить минимально возможное число сотрудников, которые могли допустить ошибку при подаче информации.

Разбор решения

Изначально, если главный сотрудник сообщил, что у него есть начальники, заменим as на ноль. Если есть сотрудники, которые не являются главными, но сообщили число 0, будем считать, что они сообщили какое-нибудь число, большее, чем могли сообщить остальные сотрудники, например n.

Обязательно должен быть сотрудник, у которого ровно один начальник. Если такого нет, возьмем сотрудника, который сообщил максимальное число (учитывая все описанное выше), и заменим это число на единицу. Аналогичную операцию нужно выполнить для числа 2, 3 и так далее, до тех пор, пока остаются сотрудники, которых мы еще не рассмотрели.

После того, как все сотрудники рассмотрены, осталось посчитать количество сотрудников, чьи числа были изменены — это и будет ответом.

729F — Игра финансистов

Финансистам Игорю и Жене стало скучно вечером, и они решили сыграть в игру. Для этого они приготовили n ценных бумаг, в которых содержится информация о доходе предприятия за какие-то промежутки времени. Обратите внимание, что доход может быть и положительным, и нулевым, и даже отрицательным.

Игорь и Женя выложили все бумаги в ряд и решили ходить по очереди. Игорь будет брать бумаги слева, а Женя справа. Первым ходит Игорь и берет 1 или 2 по своему выбору ценные бумаги слева. Далее, во время очередного хода игрок может взять k или k + 1 бумагу со своей стороны, если игрок, ходивший перед ним, взял ровно k бумаг. Ход пропускать не может ни один из игроков. Игра заканчивается, когда закончатся бумаги на столе, либо когда игрок не сможет сделать ход.

Перед вами стоит задача определить разность между суммой доходов бумаг, которые забрал себе Игорь, и суммой доходов бумаг, которые забрал себе Женя, если оба игрока играют оптимально. Игорь хочет максимизировать разность, а Женя — минимизировать.

Разбор решения

Будем решать задачу методом динамического программирования. Достаточно понятно, что позиция характеризуется тремя числами: границами отрезка бумаг, которые все еще лежат на столе, и количеством бумаг, которые взял предыдущий игрок; а также очередностью хода. Поэтому пусть Ilrk — это результат игры, если бы на столе изначально лежали только бумаги с l по r, первым ходил Игорь, и делал бы ход на k или k + 1. Аналогично, пусть Zlrk — то же, но первым ходит Женя. Ясно, что в общем случае:

Надо аккуратно обработать случаи, когда игрок не может забрать нужное число бумаг. Ответ на задачу — значение I1n1.

На первый взгляд кажется, что такое решение имеет асимптотику O(n3). Однако при пристальном рассмотрении это не так. Какие значения могут принимать l, r и k?

Во-первых, (k(k+1))/2 ≤ n, т. к. если последний игрок взял k бумаг, то всего взято уже не менее 1 + 2 + 3 + … + k = (k(k+1))/2 бумаг. Отсюда, k не превышает √(2n).
Во-вторых, посмотрим на разность числа бумаг, взятых Женей и Игорем, то есть на величину d = (n - r) - (l - 1). Пусть при этом игроки сделали поровну ходов, то есть сейчас ходит Игорь. Тогда 0 ≤ d ≤ k - 1. Действительно, на каждом ходу Женя берет либо столько же бумаг, сколько и Игорь, либо на одну больше, при этом увеличивается “длина” хода. Всего длина хода увеличилась на k - 1, а значит, эта разность не больше k - 1. Таким образом, мы можем нумеровать состояния числами l, d и k, при этом всего состояний O(n2). Состояния, в которых ход Жени, не будем рассматривать, а сразу добавим в переход и перебор обоих возможных ответных ходов (всего четыре перехода). Итоговая асимптотика O(n2), при этом проще всего реализовать данное решение с помощью рекурсивного перебора с запоминанием.

737E — Тане – 5 лет!

Тане исполнилось 5 лет и все её друзья собрались на праздновании дня рождения. Всего, включая Таню, на празднике присутствуют n детишек.

Праздник уже подходит к концу, но напоследок запланированы игровые автоматы. В зале, где проходит праздник, есть m игровых автоматов, которые пронумерованы от 1 до m. Каждый из детей уже составил список тех автоматов, в которые он хочет поиграть. Более того, если ребенок хочет поиграть на каком-то автомате, то он знает точно, сколько ему надо времени, чтобы насладиться игрой на нём. На любом автомате единовременно может играть только один ребенок.

Так как праздник уже затянулся, то все взрослые гости уже хотят по домам. Чтобы ускорить процесс вы можете дополнительно заказывать вторые экземпляры автоматов, для того чтобы арендовать второй экземпляр автомата j надо заплатить pj бурлей. Арендовав автомат, его можно использовать до конца праздника.

Как скоро все дети смогут поиграть в соответствии со своими пожеланиями, если у вас есть бюджет b бурлей на аренду дополнительных автоматов. Для каждого автомата в наличии есть только один запасной, так что арендовать третий экземпляр автомата нельзя.

Дети могут прерываться во время игры произвольным образом. Если i-й ребенок хочет поиграть на j-м автомате, то после аренды еще одного автомата j допустимо, что часть времени он сыграет на основном экземпляре j-го автомата, а часть — на дополнительном (причем любая из этих частей может выродиться в пустую). Переключение между автоматами может происходить мгновенно в целочисленные моменты времени. Конечно, ребенок не может играть на двух автоматах одновременно.

Помните, что цели сэкономить нет (на детях не экономят!), требуется минимизировать время окончания игры последнего из детей.

Разбор решения

Сначала решим задачу в упрощенной формулировке: пусть не существует никаких дубликатов автоматов (или, иначе говоря, что бюджета b не хватает на аренду любого из дубликатов).

Можно считать, что каждый ребенок хочет поиграть в каждый из автоматов. Действительно, просто будем считать, что в этом случае ti, j = 0. Таким образом, можно считать, что значения t представляют собой прямоугольную таблицу — для каждой пары ребенок/автомат в ячейке записано время игры.

Очевидно, что минимальное время, когда все игры подойдут к концу, не меньше суммы значений в каждой из строк Ri = ti, 1 + ti, 2 + … + ti, m. Аналогично, так как на каждом автомате единовременно играет не более одного ребенка, то минимальное время, когда все игры подойдут к концу не меньше суммы значений в каждом из столбцов Cj = t1, j + t2, j + … + tn, j.

Следовательно, минимальное время не меньше max(R1, R2, …, Rn, C1, C2, …, Cm). На самом деле всегда существует такое расписание, что искомое минимальное время равно максимуму из всех сумм по строкам и всем сумм по столбцам. Назовем эту величину буквой T.

Покажем этот факт, а заодно и предложим способ нахождения искомого расписания.

Построим взвешенный двудольный граф, в каждой доле которого n + m вершин.

Представим, что у каждого автомата есть вымышленный ребенок, то есть теперь детей становится n + m (n настоящих и m вымышленных). Вершины первой доли будут соответствовать детям: u1, u2, …, un — вершины, соответствующие настоящим детям, и un + 1, un + 2, …, un + m — вершины, соответствующие вымышленным детям, причем un + j — это вымышленный ребенок автомата j.

Аналогично, представим, что у каждого ребенка есть вымышленный автомат (их будет n). Вершины второй доли будут соответствовать автоматам: первые m вершин настоящим — обозначим их как v1, v2, …, vm, а следующие n вымышленным — vm + 1, vm + 2, …, vm + n. Вершина vm + i будет соответствовать вымышленному автомату ребенка i.

Проведем ребра. У нас будет четыре типа ребер:

1. между настоящими детьми и настоящими автоматами,
2. между вымышленными детьми и настоящими автоматами,
3. между настоящими детьми и вымышленными автоматами,
4. между вымышленными детьми и вымышленными автоматами.

Ребра будем проводить так, чтобы сумма весов инцидентных ребер для каждой вершины оказалась равна T.

Ребра типа 1. Будем проводить ребро между ui и vj, если ti, j > 0. Вес ребра назначим ti, j. Наличие такого ребра и обозначает, что ребенок должен поиграть на автомате нужное количество минут.

Ребра типа 2. Наличие такого ребра и обозначает, что автомат будет иметь вынужденный простой в некоторое количество минут (иными словами, на нем будет в это время играть вымышленный ребенок этого автомата). Для всех j от 1 до m найдем a - Cj. Если эта величина положительна, то проведем ребро между un + j и vj такого веса.

Ребра типа 3. Наличие такого ребра и обозначает, что ребенок будет иметь вынужденный простой в некоторое количество минут (можно считать, что ребенок это время играет на вымышленном автомате). Для всех i от 1 до n найдем a - Ri. Если эта величина положительна, то проведем ребро между ui и vm + i такого веса.

Ребра типа 4. После добавления ребер типов 1-3 очевидно, что суммы весов инцидентных ребер для всех вершин u1, u2, …, un, v1, v2, …, vm в точности равна T. Для вершин же un + 1, un + 2, …, un + m, vm + 1, vm + 2, …, vm + n такая сумма пока меньше либо равна T. Добавим серию ребер между этими вершинами так, чтобы сделать и эти суммы равными T. Это всегда можно сделать, просто жадно добавляя такие ребра.

Известен следующий факт: в произвольном регулярном двудольном графе существует совершенное паросочетание (следствие теоремы Холла).

Если посмотреть на данный нам граф как на невзвешенный мультиграф (граф с кратными ребрами), где вес ребра в нашем графе обозначает количество ребер между парой вершин, то получившийся граф будет регулярным графом и для него будет верен факт выше (то есть будет существовать совершенное паросочетание).

Найдем совершенное паросочетание алгоритмом Куна во взвешенном графе (как показано выше оно обязательно найдется). Выберем вес минимального ребра в нем, пусть эта величина равна M. Тогда назначим детей на автоматы для каждого ребра между вершинами u1, u2, …, un и v1, v2, …, vm на время M. Кроме того, из веса каждого ребра паросочетания вычтем M. Если вес ребра стал равен 0, то удалим ребро.

После этого граф останется таким, что сумма весов ребер для каждой вершины — константа. Значит в нем опять есть совершенное паросочетание. Проделаем с ним ту же операцию.

Будем так действовать, пока в графе есть хотя бы одно ребро. Найденное расписание — искомое.

На самом деле для ускорения в этой части решения можно не искать каждый раз с нуля паросочетание, а достраивать из ненасыщенных вершин первой доли, если такие находятся. Этот алгоритм суммарно будет работать за O(e2), где e — это первоначальное количество ребер, то есть e = O(nm), то есть асимптотика алгоритма становится O(n2m2). Конкретно в этой задаче ограничения были маленькие, и строить паросочетания можно было каждый раз с нуля алгоритмом Куна.

Кроме того, на самом деле мы строим оптимальную покраску двудольного графа. Наверное, для ее нахождения можно просто применить известный алгоритм (почитайте про оптимальную реберную покраску двудольного графа).

Итак, мы решили задачу без аренды дубликатов автоматов. Кроме того, величину ответа можно найти совсем просто как максимум из всех сумм по строкам и всем сумм по столбцам матрицы времен ребенок/автомат.

Если допустимы аренды дубликатов, то они эквивалентны добавлению столбца, в который можно распределить частично значения из данного столбца. Конечно, выгодно делать такое со столбцом если сумма по нему Cj = T (то есть в него упирается ответ). Такое имеет смысл делать только одновременно со всеми столбцами, для которых Cj = T.

Поэтому этап определения, какие автоматы надо арендовать, выглядит так. Посчитаем сумму арендных плат для всех автоматов, что Cj = T. Если эта величина меньше или равна бюджету b, то арендуем все эти автоматы. Добавим соответствующие столбцы в таблицу, раскидав максимально поровну в них значения из дублируемых столбцов. Пересчитаем T. Повторим процесс и прервем его, когда сумма арендных плат за очередную операцию больше b.

737F — Грязные тарелки

После очередного праздника у Никиты на кухне образовалась стопка грязных тарелок. Их надо помыть и поставить в сушилку, при этом в сушилке тарелки тоже должны стоять в стопке, причем размеры тарелок должны возрастать сверху вниз. Все размеры тарелок различны.

У Никиты не очень много свободного места, а именно, есть место только для еще одной стопки тарелок. Поэтому он может выполнять лишь две операции:

Взять любое количество от 1 до a верхних тарелок из стопки с грязными тарелками, помыть их и положить в том же порядке на верх промежуточной стопки.
Взять любое количество от 1 до b верхних тарелок из промежуточной стопки и положить в том же порядке на верх стопки в сушилке.
Обратите внимание, что при выполнении любой из операций тарелки кладутся на стопку в том же порядке, в каком они были перед выполнением операции.

Вам известны размеры тарелок s1, s2, …, sn в порядке их лежания в стопке с грязными тарелками сверху вниз, а также числа a и b. Все размеры тарелок различны. Напишите программу, которая будет определять, может ли Никита расположить все тарелки в сушилке в возрастающем сверху вниз порядке, и если может, то найдите какой-нибудь, не обязательно оптимальный, порядок действий для этого.

Разбор решения

Для начала попробуем решить задачу, когда нет ограничений на a и b. Понятно, что если так переложить нельзя, то нельзя и с ограниченными a и b.

Рассмотрим, какие операции можно и нельзя совершать. Понятно, что нельзя переносить на стопку в сушилке тарелки не по порядку, т. к. убрать мы их оттуда не можем. Также ясно, что если в какой-то момент мы можем перенести некоторую последовательность тарелок с верха промежуточной стопки на верх итоговой стопки, и они займут там правильное место, то это можно сделать прямо сейчас. То же относится и к стопке с грязной посудой, но это займет две операции. Также, легко заметить еще одну ситуацию, попав в которую, мы уже не сможем дойти до ответа: если в промежуточной стопке непосредственно на тарелке размера x лежит тарелка размера y, и y < x - 1. Действительно, ни при какой последовательности действий мы не сможем вставить между ними “недостающие” тарелки. Назовем положение тупиковым, если в нем сложилась такая ситуация.

Назовем операцию, которая перемещает тарелки в сушилку так, что они там располагаются на правильных местах, выкладыванием. Т. к. выкладывание можно производить в любой момент, то будем после каждой операции проверять возможность такой операции и производить ее, если можно. Далее будем разбирать ситуации, когда выкладывание невозможно.

Назовем последовательность тарелок почти убывающей, если она состоит из одного или нескольких блоков тарелок, в каждом из которых размеры тарелок – последовательные целые числа, при этом в каждом следующем блоке все размеры меньше, чем в предыдущем. Иначе говоря, почти убывающая последовательность выглядит так: x1, x1 + 1, x1 + 2, …, y1, x2, x2 + 1, x2 + 2, …, y2, x3, …, при этом x1 > y2, x2 > y3 и так далее. Рассмотрим максимальную последовательность тарелок сверху грязной стопки, являющуюся почти убывающей последовательностью. Понятно, что до того, как мы перенесем всю стопку, операция, переносящая в промежуточную стопку что-то кроме элементов этой последовательности, создаст тупиковое положение, т. к. размер последней тарелки в этой последовательности хотя бы на 2 меньше размера следующей тарелки. Также понятно, что мы не сможем сделать выкладывание до того, как перенесем всю последовательность в промежуточную стопку. Так или иначе, единственно возможные ближайшие действия это перенести эту последовательность в промежуточную стопку, вопрос только в каком порядке. Возможны два случая:

• Размеры тарелок в этой последовательности образуют непрерывный отрезок целых чисел, иными словами, y2 = x1 - 1, y3 = x2 - 1 и т. д.. В таком случае мы можем перекладывать блоки последовательно на промежуточную стопку, чтобы иметь возможность потом перенести целиком. Очевидно, тупикового положения внутри последовательности не образуется. Если оно образовалось на стыке с тем, что лежит ниже, то оно бы образовалось и при любом другом переносе этой стопки. Аналогичное утверждение можно сделать про верхний стык с тем, что мы позже положим сверху. Значит, такой перенос оптимален, давайте его выполним.
• Есть “дырки” во множестве размеров тарелок в последовательности. Тогда можно заметить, что, если мы не перенесем всю последовательность одной операцией в промежуточную стопку в том же порядке, то в процессе переноса этой последовательности в любом другом порядке мы обязательно попадем в тупиковое положение. Строго можно это показать, предположив, что мы перенесли какую-то часть последовательности, которая была ниже “дырки”, выше нее, или же наоборот. В таком случае нам ничего не остается, кроме как переместить всю последовательность целиком.

Видно, что мы в каждой ситуации нашли оптимальный ход, а значит, решать задачу с a = b = ∞ можно, моделируя эти оптимальные ходы за O(n2), или, при желании, за O(n). Если в конце все тарелки окажутся в сушилке, то мы нашли решение, иначе решения нет.

Теперь разберемся с ограничениями на a и b. Операцию выкладывания из грязной стопки по-прежнему можно осуществлять, перекладывая тарелки по одной в промежуточную стопку, и затем снова по одной в сушилку. Выкладывание из промежуточной стопки не всегда выполнимо, поэтому надо следить за размером блоков в промежуточной стопке. Однако, если есть выкладывание, которое можно выполнить, то его нужно выполнить, а если его нельзя выполнить, то мы не сможем выложить тарелки нужным образом. Поэтому далее опять будем считать, что все возможные выкладывания сделаны. Опять рассмотрим наибольшую почти убывающую последовательность в грязной стопке, и те же два случая:

• Если есть “дырки”, то, как мы уже выяснили, единственно возможной операцией является перенос всей последовательности за одну операцию. Если длина превышает a, то мы вообще никак не можем расположить тарелки в правильном порядке.
• Если “дырок” нет, то возможны варианты. Т. к. нас теперь интересует длина блоков в промежуточной последовательности, то не всегда выгодно выстраивать тарелки в возрастающем сверху вниз порядке. Рассмотрим несколько случаев:Значения a и b таковы, что мы можем выполнить с этой последовательностью то же, что и при бесконечных a и b. Тогда нужно это сделать, т. к. если сверху или снизу с этой последовательностью объединится еще один или несколько блоков, то это единственное расположение в промежуточной стопке, не являющееся тупиковым. Иначе, мы будем выкладывать ровно эту последовательность за одну операцию, а т. к. ее размер не превышает b, то все хорошо.Иначе, нужно перемещать последовательность в промежуточную стопку как-то по-другому. Пусть, для начала, длина последовательности превышает b. Рассмотрим случаи:Если в последовательности всего один блок, то нужно переложить так, чтобы последовательность убывала сверху вниз, перекладывая тарелки по одной. Действительно, сделать верхней тарелку с наименьшим размером, или сделать самой нижней тарелку с наибольшим размером (для того, чтобы было возможно объединение с соседними блоками) без допущения тупикового положения или того, что длина блока больше b, невозможно, а значит, лучше всего сделать все блоки размера 1, т. к. так мы точно сможем их выложить.В случае, если блоков больше двух, то единственный способ их переложить, чтобы не возникло тупикового положения, это переместить все вместе. Если это невозможно, то решения нет.Теперь, если блоков ровно два, то единственные последовательности перекладываний, не приводящая к тупиковому положению, это в две операции либо переложить сначала часть верхнего блока, потом все остальное, или наоборот, сначала первый блок и часть второго, затем оставшуюся часть второго. Необходимо сделать так, чтобы размер перекладываемых блоков был не больше a, а после перекладывания — не больше b (после перекладывания размеры блоков перераспределятся). Легко написать неравенства на выполнимость таких операций. Также можно проверить, что невозможно получить верхней тарелкой самую маленькую, или нижней — самую большую, поэтому эти блоки ни с чем не объединятся. Поэтому нам подойдет любая последовательность операций, удовлетворяющая неравенствам на размер перемещаемых частей.Пусть теперь b таково, что мы можем переместить всю последовательность за раз, но a меньше размера какого-то из блоков, поэтому мы не можем сделать последовательность возрастающей.Если блок всего один, то, опять же, надо просто переложить все тарелки по одной.Если блоков больше двух, то мы не можем их переложить, не допустив тупикового положения. Значит, решения не существует.Если блоков ровно два, то тут ситуация аналогична случаю с двумя блоками, когда не хватало размера b, разве что не обязательно рассматривать ограничения на размер блока после перекладывания (т. к. он будет меньше b).

Таким образом, опять же, на каждом шаге у нас есть оптимальный ход. Решение — моделировать оптимальные ходы. Можно реализовать за O(n), но, чтобы не запутывать излишними действиями, были даны ограничения, позволяющие написать решение за O(n2).

Mail.Ru Group, МГТУ им. Н. Э. Баумана и МФТИ благодарят за помощь в организации и проведении чемпионата своих партнеров: Сodeforces, Мел, GeekBrains, Tproger.ru, Абитуриент.про, Учеба.ру, Решу ЕГЭ, GeekTime.