Задача про воду, накапливающуюся между стенами

Эту задачу задавали на собеседовании в Twitter.

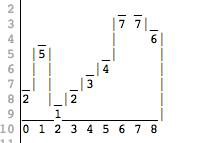
Рассмотрим следующую картинку:

На этой картинке изображены стены различной высоты в некотором плоском мире. Картинка представлена массивом целых чисел, где индекс — это точка на оси X, а значение каждого индекса — это высота стены (значение по оси Y). Картинке выше соответствует массив [2, 5, 1, 2, 3, 4, 7, 7, 6].

Теперь представьте, что начался дождь, который не прекращается и поливает стены сверху равномерным потоком. Сколько воды соберется в «лужах» между стенами?

Единицей объема воды считаем квадратный блок 1×1. На картинке выше всё, что расположено слева от точки 1, выплескивается. Вода справа от точки 7 также прольется. У нас остается лужа между 1 и 6 — таким образом, получившийся объем воды равен 10.

Первый вариант решения (неверный)

Можно предположить, что нужно найти локальные максимумы и подсчитать пространство между ними, заполненное водой. Алгоритм будет довольно простой, но ответ на самом деле некорректен.

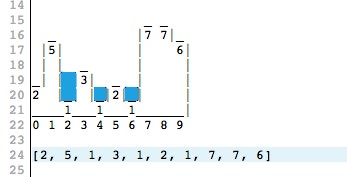
Рассмотрим пример:

Решение будет таким:

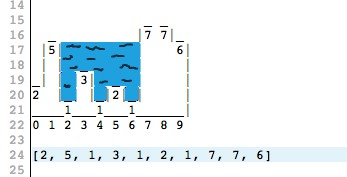
Хотя на самом деле должно быть таким:

Правильный вариант решения

Если мы проходим по списку слева направо, количество воды в каждом индексе будет не больше абсолютного максимума, который мы обнаружим заранее. Это означает, что если мы точно знаем, что есть что-то большее или равное где-то справа, то мы можем точно определить, сколько воды мы можем удержать без выплескивания. То же справедливо и для противоположного направления: если мы знаем, что нашли слева стену выше самой высокой в правой части, то это означает, что мы с уверенностью можем заполнить ее водой.

Итак, теперь решение выглядит следующим образом: найти абсолютный максимум, после чего пройти слева до максимума и затем пройти справа до максимума. Это решение требует два прохода: один для поиска максимума, и второй — разбитый на две части.

Решение в приведенном ниже коде работает в один проход, избегая поиска максимума проходом двух «указателей» навстречу друг другу с противоположных концов массива. Если наибольшее значение, найденное слева от левого указателя меньше, чем наибольшее значение найденное справа от правого указателя, то мы сдвигаем левый указатель на один индекс вправо. В противном случае, двигаем правый указатель на один индекс влево. Повторяем до тех пор, пока два указателя не пересекутся. (На словах звучит запутанно, код на самом деле очень простой).

Вариант реализации на Java

			/* package whatever; // don't place package name! */

import java.util.*;
import java.lang.*;
import java.io.*;

/* Name of the class has to be "Main" only if the class is public. */
class Ideone
{
	public static void main (String[] args) throws java.lang.Exception
	{
		int[] myIntArray = {2, 5, 1, 2, 3, 4, 7, 7, 6}; 
		System.out.println(calculateVolume(myIntArray));
	}
	
	public static int calculateVolume(int[] land) {
		
		int leftMax = 0;
		int rightMax = 0;
		int left = 0;
		int right = land.length - 1;
		int volume = 0;
		
		while(left < right) {
			if(land[left] > leftMax) {
				leftMax = land[left];
			}
			if(land[right] > rightMax) {
				rightMax = land[right];
			}
			if(leftMax >= rightMax) {
				volume += rightMax - land[right];
				right--;
			} else {
				volume += leftMax - land[left];
				left++;
			}
		}
		return volume;
	}
}
		

Для тех, кто предпочитает Gist.