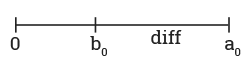Напишите функцию, меняющую местами значения переменных, не используя временные переменные

Это классическая задача, которую любят предлагать на собеседованиях, и она достаточно проста. Пусть a0 — это исходное значение a, а b0 — исходное значение b. Обозначим diff разницу а0 - b0.

Давайте покажем взаимное расположение всех этих значений на числовой оси для случая, когда a > b:

Присвоим а значение diff. Если сложить значение b и diff, то мы получим a0 (результат следует сохранить в b). Теперь у нас b = а0 и a = diff. Все, что нам остается сделать, — присвоить b значение а0 - diff, а это значение представляет собой b - a.

Приведенный далее код реализует этот алгоритм:

			public static void swap(int a, int b) {
	// Пример для a = 9, b = 4
	a = a - b; // a = 9 - 4 = 5
	b = a + b; // b = 5 + 4 = 9
	a = b - a; // a = 9 - 5

	System.out.println("a: " + a);
	System.out.println("b: " + b);
}
		

Можно решить эту задачу с помощью битовой манипуляции. Такой подход позволит нам работать с разными типами данных, а не только с integer.

			public static void swap_opt(int a, int b) {
	//Пример для a = 101 (в двоичной системе) и b = 110
	a = a ^ b; // a = 101^110 = 011
	b = a ^ b; // b = 011^110 = 101
	a = a ^ b; // a = 011^101 = 110

	System.out.println("a: " + a);
	System.out.println("b: " + b);
}
		

Этот код использует операцию XOR. Проще всего понять, как работает код, взглянув на два бита — р и q. Давайте обозначим как р0 и q0 исходные значения.

Если мы сможем поменять местами два бита, то алгоритм будет работать правильно. Давайте рассмотрим работу алгоритма пошагово:

1. p = p0^q0 /* 0 если р0 = q0, 1 если р0 != q0 */
2. q = p^q0 /* равно значению р0 */
3. 3. p = p^q /* равно значению q0 */

В строке 1 выполняется операция p = p0^q0, результатом которой будет 0, если p0 = q0, и 1, если p0 != q0.

В строке 2 выполняется операция q = p^q0. Давайте проанализируем оба возможных значения p. Так как мы хотим поменять местами значения p и q, в результате должен получиться 0:

• p = 0: в этом случае p0 = q0, так как нам нужно вернуть p0 или q0. XOR любого значения с 0 всегда дает исходное значение, поэтому результатом этой операции будет q0 (или p0).
• p = 1: в этом случае p0 != q0. Нам нужно получить 1, если q0 = 0, и 0, если p0 = 1. Именно такой результат получается при операции XOR любого значения с 1.

В строке 3 выполняется операция p = p^q. Давайте рассмотрим оба значения p. В результате мы хотим получить q0. Обратите внимание, что q в настоящий момент равно p0, поэтому на самом деле выполняется операция p^p0.

• p = 0: так как p0 = q0, мы хотим вернуть p0 или q0. Выполняя 0^p0, мы вернем p0(q0).
• p = 1: выполняется операция 1^p0. В результате мы получаем инверсию p0, что нам и нужно, так как p0 != q0.

Остается только присвоить p значение q0, a q — значение р0. Мы удостоверились, что наш алгоритме корректно меняет местами каждый бит, а значит, результат будет правильным.

Разбор взят из перевода книги Г. Лакман Макдауэлл и предназначен исключительно для ознакомления.Если он вам понравился, то рекомендуем купить книгу «Карьера программиста. Как устроиться на работу в Google, Microsoft или другую ведущую IT-компанию».