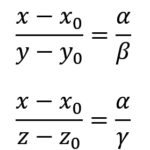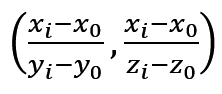Разбор задач из онлайн-соревнования по бэкенду Yandex.Taxi Coding Fest

В июле прошло онлайн-соревнование по бэкенду Yandex.Taxi Coding Fest. Перед вами задачи, которые предлагались на соревновании, и их решения с подробным разбором.

1. Группировка рекомендуемых точек подачи на прямой

Формулировка задачи

На улицу Льва Толстого заказали такси N раз. Известны точки на улице, куда подъехали водители. Назовём их точками прибытия. Приложение запоминает точки прибытия и на их основе просчитывает рекомендуемые точки подачи. Точки подачи нужны, чтобы приложение порекомендовало пользователю, куда лучше заказать автомобиль.

Сформируйте из точек прибытия на улице Льва Толстого наименьшее количество рекомендуемых точек подачи. Каждая рекомендуемая точка должна быть одной из списка точек прибытия. Расстояние от каждой точки прибытия до ближайшей рекомендуемой не должно превосходить R.

Формат ввода

В первой строке задаётся два числа N (0 ≤ N ≤ 105) и R (0 ≤ R ≤ 109) через пробел. В следующей строке записано N целых чисел (координаты точек), каждое из которых по абсолютной величине не превосходит 109.

Формат вывода

Выведите одно целое число, показывающее наименьшее количество точек, которые надо выбрать в качестве рекомендуемых точек подачи.

Примеры

Формат вывода

Выведите одно целое число, показывающее наименьшее количество точек, которые надо выбрать в качестве рекомендуемых точек подачи.

Примеры

Входные данные №1

3 2

3 5 1

Выходные данные №1

1

Входные данные №2

3 2

4 7 1

Выходные данные №2

3

Входные данные №3

6 1

6 2 4 3 5 1

Выходные данные №3

2

Разбор задачи

Для начала переведём задачу в математическую постановку.

Нужно выбрать такое наименьшее количество точек на числовой прямой, чтобы расстояние от каждой имеющейся точки до выбранной нами не превосходило R. Можно считать, что каждая выбранная нами точка вырезает на плоскости отрезок длиной 2R, и после вырезаний должны пропасть все точки. Для решения задачи нам сначала надо отсортировать точки. После сортировки у нас появляется самая левая точка. Легко доказать, что эта точка в оптимальном решении должна входить ровно в один отрезок, причём этот отрезок должен быть максимально отодвинут вправо. Чтобы выбрать наиболее подходящую точку, мы проходимся циклом по точкам слева направо и ищем самую правую, у которой расстояние до первой точки не превосходит R. Потенциально это может быть и самая правая точка.

Как только мы нашли эту точку, мы виртуально вырезаем отрезок длиной 2R и пропускаем все точки, что находятся внутри него (слева от первой и справа от последней точки отрезка).

После этого действия у нас снова остался отсортированный список точек, к которому мы применяем тот же алгоритм. Осталось посчитать, сколько точек нам удалось выбрать.

2. Такси в отеле

Формулировка задачи

При отеле в курортном городе работает такси. Оно забирает постояльцев отеля из аэропорта, а в день отъезда отвозит назад. Нам известны дни приездов и отъездов автомобилей этого такси и число клиентов отеля, которые каждый раз приезжали или уезжали. В один и тот же день может быть как несколько приездов, так и несколько отъездов посетителей.

В отеле по нечётным числам месяца готовит шеф-повар Мефодий, по чётным — шеф-повар Кирилл. Они поспорили, кому тяжелее работать. Повара хотят посчитать максимальное число посетителей, для которых готовил каждый из них с первого дня по текущий включительно.

Напишите программу, которая, используя данные про приезды и отъезды посетителей, выводит на стандартный вывод два числа через пробел. Первое число — максимальное количество посетителей, для которых готовил Мефодий. Второе — максимальное количество посетителей, для которых готовил Кирилл.

Условие: для приезжающих постояльцев в день приезда готовить нужно, а для отъезжающих в этот день — уже не нужно (то есть нужно готовить только для тех, кто остаётся в отеле как минимум на ночь). Изначально в отеле посетителей не было.

Формат ввода

На входе на первой строке есть одно число N (2 ≤ N ≤ 105), где (N − 1) — число записей в логе.

Далее следует строка с информацией про номер текущего дня M — целое положительное число (0 ≤ M ≤ 103). После идёт (N − 1) — строка с данными о приездах и отъездах такси с посетителями по текущий день в виде набора строк в следующем формате:

arrival arrival_day_number clients_count

departure departure_day_number clients_count

Строки, начинающиеся со слова arrival, соответствуют приезду clients_count клиентов в день под номером arrival_day_number.

Строки, начинающиеся со слова departure, соответствуют отъезду clients_count клиентов в день под номером departure_day_number.

При этом выполняются условия:

0 < clients_count ≤ 103

0 ≤ arrival_day_number ≤ 105

0 ≤ departure_day_number ≤ 105

Формат вывода

Два числа — максимальные количества посетителей, для которых готовили Мефодий и Кирилл соответственно.

Примеры

Входные данные

7

3

arrival 3 2

departure 2 5

arrival 3 2

arrival 2 2

arrival 1 10

departure 3 7

Выходные данные

10 7

Разбор задачи

Задача имеет несколько разных подходов к решению. Разберём один из них.

Нас просят найти два числа: максимальные количества посетителей в день, для которых готовил каждый из поваров.

Для начала считаем данные о приездах и отъездах посетителей в массив структур, каждая из которых хранит в себе информацию об одном из событий: в какой из дней был приезд или отъезд и сколько людей в этот день приехало или выехало из отеля соответственно.

Далее отсортируем этот массив событий в хронологическом порядке. После этого, чтобы посчитать интересующие нас показатели, нужно пройти по получившемуся массиву событий слева направо, поддерживая текущее число посетителей отеля, для которых нужно готовить, и обновляя два максимума — количества посетителей в чётные и нечётные дни. При этом стоит обратить внимание на два нюанса:

1. В один и тот же день может быть несколько приездов и отъездов, поэтому нужно явно посчитать, сколько людей приехало и выехало в каждый из дней, суммируя приезжающих и вычитая выезжающих.

2. Если в некоторый момент времени мы рассматриваем день с, например, чётным номером N, а на предыдущей итерации цикла был рассмотрен день с номером меньшим (N − 1), то, при условии, что текущее число посетителей отеля, для которых нужно готовить превысило максимум для нечётных дней, нужно обновить и этот максимум (по нечётным дням).

3. Очередь такси в космическом порту

Формулировка задачи

Водитель такси прибывает в космопорт Луны. Все такси в ожидании заказа выстраиваются в очередь возле шлюзов космической станции.

Считаем, что автомобили образуют очередь, если все они находятся на одной прямой. Длина очереди не может быть менее 3. Координаты автомобиля задаются тремя целыми числами. В одной точке пространства не может находиться более одного автомобиля.

Помогите водителю найти самую короткую очередь. В случае, если невозможно найти минимальную очередь длиной ≥ 3, в качестве ответа верните 0.

Формат ввода

Первая строка содержит целое неотрицательное число — количество записей с координатами такси. Каждая следующая строка состоит из трёх целых чисел, разделённых пробелами, образующих тройку координат x, y, z.

Формат вывода

Одно число — минимальная длина очереди.

Примеры

Входные данные №1

10

1 1 1

2 2 2

3 3 3

4 4 4

5 5 5

6 6 6

7 7 7

3 6 9

2 4 6

1 2 3

Выходные данные №1

3

Входные данные №2

5

1 1 1

2 2 2

3 3 3

4 1 4

9 9 9

Выходные данные №2

4

Разбор задачи

Очевидно, что задача сводится к поиску подмножеств точек, лежащих на одной прямой, и выбору подмножества минимальной мощности ≥ 3.

Вспомним каноническое уравнение прямой:

Где (α, β, γ)  – координаты вектора, коллинеарного этой прямой.

Из данного уравнения явным образом следует:

Таким образом, получаем простой алгоритм решения задачи.

На каждом шаге будем поочерёдно выбирать каждую из N точек за (x0, y0, z0). Разобьём всё остальное множество точек на подмножества по ключу 

и запомним минимальную мощность получившихся подмножеств.

С точки зрения реализации, удобно перейти от операций с рациональными дробями к операциям с тройкой целых чисел (Δxi, Δyi, Δzi).

Для этого необходимо нормировать (xi − x0, yi − y0, zi − z0) по НОД(xi − x0, yi − y0, zi − z0).

Полученный алгоритм будет иметь вычислительную сложность O(n2) и требования к памяти O(n).

4. Телепорт

Формулировка задачи

Яндекс.Такси открыло услугу межконтинентальной телепортации автомобилей. Телепорт представляет собой замкнутую область (полигон), в котором одновременно могут находиться несколько автомобилей. Телепорт открывается в определённые моменты времени — заранее они не известны. Одновременно может телепортироваться только одна машина. Если в момент открытия портала в полигоне находится более одного автомобиля, то будет телепортирован тот, который лучше всего синхронизирован с полем телепорта (дольше других непрерывно находился в зоне телепортации). Зная траектории движения автомобилей и моменты времени открытия портала, выведите соответствие порядкового номера открытия портала и автомобиля. Если в момент открытия портала в полигоне не было автомобилей, выведите -1.

Формат ввода

В первой строке находится число N — количество вершин в полигоне. В следующей строке находится N пар целых чисел Pxi и Pyi (разделённые пробелом), задающих вершины полигона. Никакие из двух сторон полигона не пересекаются. В следующей строке находится число M — количество автомобилей. Далее следует M строк, в каждой из которых идёт количество треков i-го автомобиля Ti; следом за ней — Ti * 3 целых чисел, разделённых пробелом. Каждая тройка - это одна координата автомобиля, состоящая из времени точки t и координат точки x и y. В следующей строке находится количество открытий телепорта K. За ней на этой же строке через пробел находится K чисел, обозначающих время открытия телепорта Ki. Гарантируется, что все времена будут строго возрастающими.

Ограничения:

3 ≤ N ≤ 100

-109 ≤ Pxi, Pyi, x, y ≤ 109

0 ≤ M ≤ 104

1 ≤ K ≤ 104

0 ≤ t ≤ 106

0 ≤ Ki ≤ 107

Суммарное количество всех треков Ti всех автомобилей не превышает 105, при этом каждый автомобиль имеет хотя бы один трек. У каждого автомобиля все треки гарантированно уникальные по времени. Автомобиль находится внутри полигона, если последний его трек (со временем t ≤ Ki) находится внутри полигона.

Формат вывода

Необходимо вывести K целых чисел, где каждое число обозначает идентификатор автомобиля, который телепортируется в соответствующее время, либо -1, если автомобилей в очереди нет. Если несколько автомобилей въехали одновременно, то необходимо вывести тот, у которого меньший идентификатор. Каждый автомобиль может телепортироваться не более одного раза.

Примеры

Входные данные №1

4

-1 -1 -1 1 1 1 1 -1

4

1 1 -2 1

1 2 0 0

1 3 0 0

1 4 1 1

5 0 2 4 5 6

Выходные данные №1

-1 2 3 4 -1

Входные данные №2

4

-1 -1 -1 1 1 1 1 -1

4

2 1 -2 1 3 -1 1

1 2 0 0

1 3 0 0

1 4 1 1

5 0 2 4 5 6

Выходные данные №2

-1 2 1 3 4

Разбор задачи

Рассмотрим один из подходов к решению задачи.

При считывании позиций водителей можно сразу определять принадлежность точки заданному полигону. По условию полигон не имеет никаких пересечений, поэтому задача несколько упрощается. Можно воспользоваться алгоритмом с использованием луча, выпущенного из проверяемой точки, и посчитать количество пересечений со сторонами многоугольника.

Далее можно объединить все позиции водителей с привязкой ко времени и время открытия телепорта в один сортированный список событий и пройти по нему. Тогда задача сводится к поддержанию актуального списка водителей в очереди и их последовательности.

При появлении очередного трека с координатами, проверяем, был ли этот водитель внутри полигона ранее. Если водитель только что въехал в полигон, то добавляем его в конец очереди (удобнее использовать для этого двусвязный список) и в индекс для быстрого поиска водителя внутри списка. Если водитель выехал из полигона, то по индексу находим его в списке и удаляем из списка и из индекса.

При открытии телепорта берём первого водителя из списка (или выводим -1, если список пустой) и добавляем его в список исключений, поскольку он уже переместился на другой континент.

Так как все моменты открытия телепорта строго возрастающие, нет необходимости делать дополнительные индексы, а можно выводить данные сразу по ходу новых открытий телепорта.