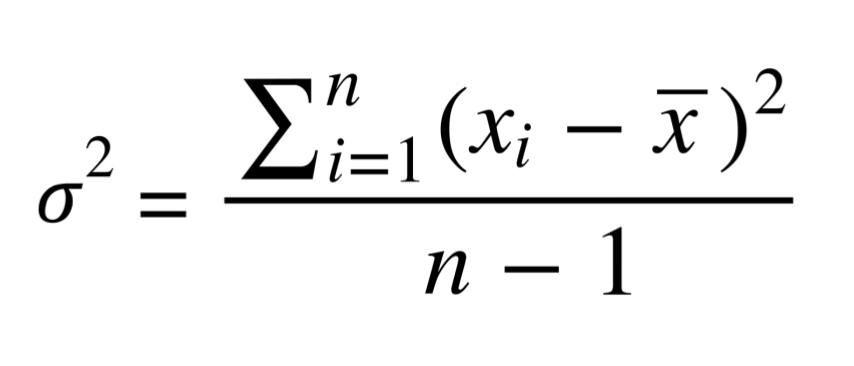Основы статистики с Python: описательная статистика

Область статистики часто понимают неправильно, однако она играет важную роль в повседневной жизни. Корректно составленная статистика позволяет извлечь знания из неопределённого и сложного реального мира, однако при неправильном применении она может нанести вред или ввести в заблуждение. Для того, чтобы отличить правду от лжи, важно чётко понимать методы статистики и значение различных статистических измерений.

В этой статье мы поговорим о:

• определении статистики;
• описательной статистике:мерах центральной тенденции;мерах разброса.

Нам не понадобятся глубокие знания статистики, однако понадобится хотя бы минимальное знание Python. Если вы не встречались с циклами for и списками, будет лучше сначала ознакомиться с ними.

Не знаете с какой стороны подойти к Python? Тогда почитайте о том, с чего начать изучение Python.

Загружаем данные

Мы будем обсуждать статистику, используя реальные данные, взятые с платформы Kaggle из датасета Wine Reviews. Сами данные были извлечены с сайта Wine Enthusiast.

Предположим, вы — ученик сомелье. Вы нашли интересный датасет и хотели бы сравнить различные вина, воспользовавшись статистикой для описания данных и сделав для себя несколько выводов.

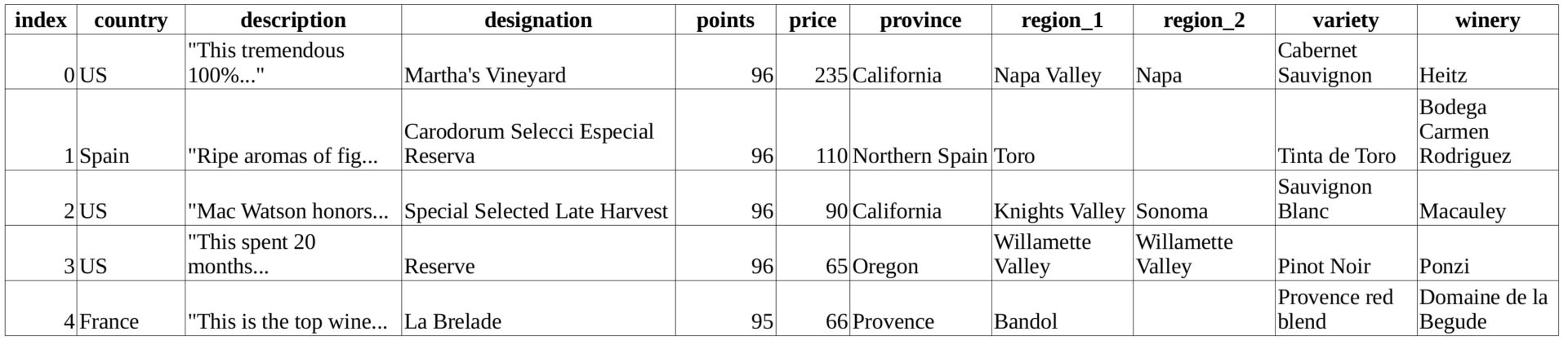
Код, представленный ниже, загружает датасет wine-data.csv в переменную wines в виде списка списков. В статье мы будем вести статистику на примере этой переменной:

			import csv
with open("wine-data.csv", "r", encoding="latin-1") as f:
    wines = list(csv.reader(f))
		

Давайте посмотрим на первые пять строк данных, указанных в таблице, чтобы понять, с какими значениями мы работаем:

Что именно представляет собой статистика?

Это вопрос с подвохом. Статистика включает в себя много всего, поэтому попытка кратко описать её неизбежно приведёт к упущению некоторых деталей. Тем не менее нам нужно с чего-то начинать.

Область статистики можно рассматривать как научную среду для работы с данными. Это определение включает все задачи, связанные со сбором, анализом и интерпретацией данных. Также статистика может относиться к отдельным измерениям, которые представляют собой сводную информацию по данным или определенные их аспекты. В этой статье мы постараемся провести грань между научной областью статистики и непосредственными измерениями.

И первым шагом будет логичный вопрос: а что такое «данные»? К счастью, это определение дать проще. Данные — это совокупность наблюдений за миром, которая может иметь множество вариаций, от качественных до количественных. Исследователи собирают данные, полученные в ходе экспериментов, предприниматели собирают данные своих клиентов, а игровые компании собирают данные о поведении игроков

Эти примеры указывают на ещё один важный аспект: наблюдения обычно связаны с генеральной совокупностью, представляющей интерес. Возвращаясь к предыдущему примеру: исследователь может рассматривать группу пациентов с определённым состоянием. Для наших данных генеральной совокупностью будет набор отзывов о винах. Чётко определив генеральную совокупность, мы можем применить методы статистики и извлечь знания из полученных результатов.

Но почему нас интересуют генеральные совокупности? Полезно иметь возможность сравнивать и противопоставлять их, чтобы проверить наши идеи. Например, мы хотели бы узнать, что пациенты, получающие новое лечение, выздоравливают быстрее тех, кто получает плацебо, но кроме того мы хотели бы доказать это количественно. Здесь на помощь приходит статистика, которая предоставляет точный подход к данным и даёт возможность принимать решения, основанные на реальных событиях, а не на догадках.

Ключевые идеи:

• статистика — наука о данных;
• данные — набор наблюдений за интересующей нас генеральной совокупностью;
• статистика предоставляет конкретный способ сравнения генеральных совокупностей с помощью чисел, а не неоднозначных описаний.

Описательная статистика

Когда у нас есть набор наблюдений, полезно свести признаки наших данных в одно определение. Этим занимается описательная статистика. Как следует из названия, описательная статистика описывает конкретное свойство данных, которые она обобщает. Такую статистику можно разделить на две категории: меры центральной тенденции и меры разброса.

Меры центральной тенденции

Меры центральной тенденции — показатели, представляющие собой ответ на вопрос: «На что похожа середина данных?». Слово «середина» звучит неточно, так как существует множество определений для её описания. Далее мы обсудим, как каждая новая мера меняет наше определение «середины».

Среднее значение

Данная характеристика описывает среднее значение в наборе данных. Вычислить её довольно просто: сложите все значения и разделите полученную сумму на количество значений.

В случае со средним значением «серединой» датасета будет среднее арифметическое его значений. Среднее значение отражает типичный показатель в наборе данных. Если мы случайно выберем один из показателей, то, скорее всего, получим значение, близкое к среднему.

Вычислить среднее значение на Python просто. Давайте выясним, чему равна средняя оценка вина в нашем датасете:

			# Извлекаем оценки из датасета
scores = [float(w[4]) for w in wines]

# Складываем все оценки
sum_score = sum(scores)

# Ищем количество оценок
num_score = len(scores)

# Считаем среднее значение
avg_score = sum_score/num_score

print(avg_score)  # выводит 87.8884184721394
		

Это среднее значение говорит нам, что «типичная» оценка в датасете равна примерно 87,8. Соответственно, большинство вин имеют высокий рейтинг, если предположить, что оценивают по шкале от 0 до 100. Тем не менее нужно учесть, что Wine Enthusiast не публикует отзывы с рейтингом ниже 80.

Есть разные типы среднего значения, но это — наиболее распространённая форма. Оно называется средним арифметическим, так как интересующие нас значения складываются.

Медиана

Следующая мера центральной тенденции, о которой пойдёт речь, — медиана. Медиана, как и среднее значение, нужна для определения типичного значения в наборе данных, но при этом не требует вычислений.

Чтобы найти медиану, данные нужно расположить в порядке возрастания. Медианой будет значение, которое совпадает с серединой набора данных. Если количество значений чётное, то берётся среднее двух значений, которые «окружают» середину.

Стандартной библиотекой Python не предусмотрен поиск медианы, но мы можем написать свою реализацию, следуя описанному алгоритму. Попробуем найти медиану цен на вина:

			# Извлекаем цены
prices = [float(w[5]) for w in wines if w[5] != ""]

# Находим их количество
num_wines = len(prices)

# Сортируем в порядке возрастания
sorted_prices = sorted(prices)

# Ищем индекс среднего элемента
middle = (num_wines / 2) + 0.5

# Находим медиану
print(sorted_prices[middle])  # 24
		

Прим.перев. С версии Python 3.4 есть встроенный способ поиска медианного значения.

Медианная цена бутылки вина составляет 24$. Это предполагает, что как минимум у половины вин в датасете цена равна или ниже 24$. Неплохо! А что насчёт среднего значения? Учитывая, что и медиана, и среднее значение отражают типичное значение, можно предположить, что они должны быть примерно одинаковы:

			print(sum(prices)/len(prices))  # 33.13
		

Средняя цена в 33,13$ на порядок выше медианной. Как это произошло? Разница между медианой и средним значением существует из-за робастности (выбросоустойчивости).

Проблема выбросов

Как вы помните, среднее значение можно найти, сложив все значения и разделив сумму на их количество, в то время как медиана ищется простой перестановкой значений. Если в данных есть выбросы — значения, которые гораздо выше или ниже остальных, — это может негативно повлиять на среднее значение. Таким образом, среднее значение не робастно, а медиана — напротив, выбросоустойчива.

Давайте взглянем на максимальную и минимальную цену в наших данных:

			min_price = min(prices)
max_price = max(prices)
print(min_price, max_price)  # 4.0, 2300.0
		

Теперь мы знаем, что в данных есть выбросы. Выбросы могут отражать интересные события или ошибки в нашем наборе данных, поэтому важно уметь определять их наличие. Сравнение медианы и моды — один из способов определить наличие выбросов, хотя визуализация обычно позволяет сделать это быстрее.

Мода

Это последняя мера центральной тенденции, о которой пойдёт речь. Мода определяется как значение, которое наиболее часто встречается в наборе данных. Мода не так очевидно соответствует понятию «середины» как среднее значение или медиана, но это соответствие абсолютно обосновано: если значение появляется в данных неоднократно, оно приблизит среднее значение к моде. Чем чаще появляется значение, тем сильнее оно влияет на среднее. Таким образом, мода показывает наиболее значимый фактор, формирующий среднее значение.

Как и в случае с медианой, встроенной функции для поиска моды у Python нет. Зато мы можем вычислить её сами, посчитав количество повторений различных цен и выбрав самую частую:

			# Создаём пустой словарь, в котором будем считать количество появлений цен
price_counts = {}
for p in prices:
    if p not in price_counts:
        counts[p] = 1
    else:
        counts[p] += 1

# Проходимся по словарю и ищем максимальное количество повторений
maxp = 0
mode_price = None
for k, v in counts.items():
    if maxp < v:
        maxp = v
        mode_price = k
print(mode_price, maxp)  # 20.0, 7860
		

Прим.перев. На самом деле, с версии Python 3.4 можно найти и моду.

Мода относительно близка к медиане, поэтому можно уверенно сказать, что и мода, и медиана отражают средние значения цен на вино.

Меры центральной тенденции полезны для описания среднего значения данных. Тем не менее они не показывают, насколько большой разброс присутствует в данных. Здесь на помощь приходят меры разброса данных.

Меры разброса данных

Меры разброса отвечают на вопрос: «Как сильно варьируются мои данные?». В мире существует не так много вещей, которые остаются в одном и том же состоянии при каждом наблюдении. Эта изменчивость делает мир нечётким и неопределённым, поэтому полезно иметь показатели, которые могут обобщить эту «нечёткость».

Размах

Наша первая мера разброса — размах. Из всех измерений, которые мы рассмотрим далее, его вычислить проще всего. Для этого нужно просто вычесть из наибольшего значения в наборе данных наименьшее.

Мы нашли максимальную и минимальную цены, когда искали медиану, поэтому сейчас можем использовать их:

			price_range = max_price - min_price
print(price_range)  # 2296.0
		

Итак, размах равен 2296, но что это значит? Когда мы рассматриваем результаты различных измерений, очень важно делать это в контексте наших данных. Наша медианная цена была 24$, а размах равен 2296$. Размах на два порядка больше медианы, что указывает на сильный разброс данных. Возможно, будь у нас ещё один винный датасет, мы могли бы сравнить размахи, чтобы понять, как они отличаются. В ином случае сам по себе размах не слишком полезен.

Мы скорее хотели бы узнать, как сильно данные отличаются от типичного значения. Здесь нам помогут стандартное отклонение и дисперсия случайной величины.

Стандартное отклонение

Стандартное отклонение тоже является мерой разброса данных. Оно помогает узнать, как сильно данные отличаются от типичного значения. Иными словами, оно говорит о том, как сильно данные отличаются от среднего арифметического. Отношение к среднему арифметическому хорошо видно при расчёте отклонения:

Поговорим немного о строении уравнения. Как вы помните, среднее арифметическое рассчитывается путём сложения всех значений и деления на их количество. Уравнение стандартного отклонения похоже, но используется, чтобы найти, на сколько в среднем значения отклоняются от типичного, и включает дополнительную операцию с извлечением корня.

В некоторых источниках можно увидеть в качестве знаменателя n вместо n-1. Такие детали выходят за рамки нашей статьи, но знайте, что использование n-1 считается более корректным. Можете прочитать интуитивное объяснение коррекции Бесселя.

Мы хотим посчитать стандартное отклонение, чтобы более полно описать цены вин и их оценки, поэтому напишем свою функцию. Поиск кумулятивной суммы вручную выглядел бы довольно громоздко, но циклы for в Python всё упрощают. Мы пишем свою функцию, чтобы показать, что на Python легко заниматься такой статистикой. Тем не менее в библиотеке numpy тоже реализовано вычисление стандартного отклонения через функцию std:

			def stdev(nums):
    diffs = 0
    avg = sum(nums)/len(nums)
    for n in nums:
        diffs += (n - avg)**(2)
    return (diffs/(len(nums)-1))**(0.5)

print(stdev(scores))  # 3.2223917589832167

print(stdev(prices))  # 36.32240385925089
		

Такие результаты вполне ожидаемы. Оценки варьируются от 80 до 100, поэтому можно предположить, что стандартное отклонение будет небольшим. С другой стороны, отклонение в ценах гораздо выше из-за выбросов. Чем больше стандартное отклонение, тем больше рассеяны данные вокруг среднего значения, и наоборот.

Далее мы увидим, что дисперсия тесно связана со стандартным отклонением.

Дисперсия

Часто стандартное отклонение и дисперсию связывают вместе и делают это не без причины. Вот уравнение дисперсии, ничего не напоминает?

Дисперсия и стандартное отклонение — почти одно и то же! Дисперсия — просто квадрат стандартного отклонения. Более того, обе величины отражают одну и ту же вещь — меру разброса, хотя стоит отметить, что единицы измерения разные. В каких бы единицах ни измерялись ваши данные, единицы измерения отклонения будут такими же, а у дисперсии они будут возведены в квадрат.

Многие новички в статистике задают вопрос: «Зачем возводить отклонение в квадрат? Разве нельзя избавится от отрицательных слагаемых при помощи модуля?». Избавление от отрицательных значений — хорошая причина для возведения в квадрат, но не единственная. Как и на среднее значение, на дисперсию и стандартное отклонение влияют выбросы. Очень часто нас интересуют выбросы, поэтому возведение в квадрат позволяет выделить эту особенность. Если вы знакомы с математическим анализом, то поймете, что наличие экспоненциального выражения позволяет найти точку минимального отклонения.

Чаще всего при статистическом анализе нам понадобятся только среднее значение и стандартное отклонение, однако дисперсия по-прежнему важна в других академических областях. Меры центральной тенденции и разброса позволяют нам систематизировать данные и извлечь из них знания.

Ключевые идеи:

• описательная статистика используется для систематизации и количественного описания данных;
• среднее значение указывает на типичное значение в нашем наборе данных. Оно не робастно;
• медиана является центральным значением в ряду данных. Она робастна;
• мода — значение, которое появляется наиболее часто;
• размах — это разность между максимальным и минимальным значениями в наборе данных;
• дисперсия и стандартное отклонение являются средним расстоянием от среднего арифметического значения.