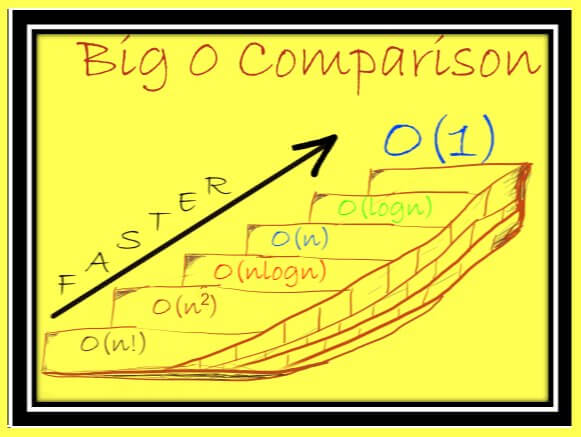
Сколько стоят операции над list, set и dict в Python? Разбираемся с временной сложностью

Автор перевода Иван Капцов

Программисту, работающему с данными, крайне важно выбирать правильные структуры данных для решения поставленной задачи, ведь выбор неправильного типа данных плохо влияет на производительность приложения. В этой статье объясняется нотация «О» большое и сложность ключевых операций структур данных в CPython.

Что означает нотация «O» большое?

В алгоритме выполняется ряд операций. Эти операции могут включать в себя итерацию по коллекции, копирование элемента или всей коллекции, добавление элемента в коллекцию, вставку элемента в начало или конец коллекции, удаление элемента или обновление элемента в коллекции.

«O» большое служит обозначением временной сложности операций алгоритма. Она показывает, сколько времени потребуется алгоритму для вычисления требуемой операции. Можно также измерить пространственную сложность (сколько места занимает алгоритм), но в этой статье мы сосредоточимся на временной.

Проще говоря, нотация «O» большое — это способ измерения производительности операции на основе размера ввода, известного как n.

Значения нотации «О» большое

На письме временная сложность алгоритма обозначается как O(n), где n — размер входной коллекции.

O(1)

Обозначение константной временной сложности. Независимо от размера коллекции, время, необходимое для выполнения операции, константно. Это обозначение константной временной сложности. Эти операции выполняются настолько быстро, насколько возможно. Например, операции, которые проверяют, есть ли внутри коллекции элементы, имеют сложность O(1).

O(log n)

Обозначение логарифмической временной сложности. В этом случае когда размер коллекции увеличивается, время, необходимое для выполнения операции, логарифмически увеличивается. Эту сложность имеют потенциально оптимизированные алгоритмы поиска.

O(n)

Обозначение линейной временной сложности. Время, необходимое для выполнения операции, прямо и линейно пропорционально количеству элементов в коллекции. Это обозначение линейной временной сложности. Это что-то среднее с точки зрения производительности. Например, если мы хотим суммировать все элементы в коллекции, нужно будет выполнить итерацию по коллекции. Следовательно, итерация коллекции является операцией O(n).

O(n log n)

Обозначение квазилинейной временной сложности. Скорость выполнения операции является квазилинейной функцией числа элементов в коллекции. Временная сложность оптимизированного алгоритма сортировки обычно равна O(n log n).

O(n^2)

Обозначение квадратичной временной сложности. Время, необходимое для выполнения операции, пропорционально квадрату элементов в коллекции.

O(n!)

Обозначение факториальной временной сложности. Каждая операция требует вычисления всех перестановок коллекции, следовательно требуемое время выполнения операции является факториалом размера входной коллекции. Это очень медленно.

Нотация «O» большое относительна. Она не зависит от машины, игнорирует константы и понятна широкой аудитории, включая математиков, технологов, специалистов по данным и т. д.

Благоприятные, средние и худшие случаи

При вычислении временной сложности операции можно получить сложность на основе благоприятного, среднего или худшего случая.

Благоприятный случай. Как следует из названия, это сценарий, когда структуры данных и элементы в коллекции вместе с параметрами находятся в оптимальном состоянии. Например, мы хотим найти элемент в коллекции. Если этот элемент оказывается первым элементом коллекции, то это лучший сценарий для операции.

Средний случай. Определяем сложность на основе распределения значений входных данных.

Худший случай. Структуры данных и элементы в коллекции вместе с параметрами находятся в наиболее неоптимальном состоянии. Например, худший случай для операции, которой требуется найти элемент в большой коллекции в виде списка — когда искомый элемент находится в самом конце, а алгоритм перебирает коллекцию с самого начала.

Коллекции Python и их временная сложность

Список (list)

Список является одной из самых важных структур данных в Python. Можно использовать списки для создания стека или очереди. Списки — это упорядоченные и изменяемые коллекции, которые можно обновлять по желанию.

Операции списка и их временная сложность

Вставка: O(n).
Получение элемента: O(1).
Удаление элемента: O(n).
Проход: O(n).
Получение длины: O(1).

Множество (set)

Множества также являются одними из наиболее используемых типов данных в Python. Множество представляет собой неупорядоченную коллекцию. Множество не допускает дублирования, и, следовательно, каждый элемент в множестве уникален. Множество поддерживает множество математических операций, таких как объединение, разность, пересечение и так далее.

Операции с множествами и их временная сложность

Проверить наличие элемента в множестве: O(1).
Отличие множества A от B: O(длина A).
Пересечение множеств A и B: O(минимальная длина A или B).
Объединение множеств A и B: O(N) , где N это длина (A) + длина (B).

Словарь (dict)

Словарь — это коллекция пар ключ-значение. Ключи в словаре уникальны, чтобы предотвратить коллизию элементов. Это чрезвычайно полезная структура данных.

Словари индексируются по ключам, которые могут быть строками, числами или даже кортежами со строками, числами или кортежами. Над словарём можно выполнить ряд операций, таких как сохранение значения для ключа, извлечение элемента на основе ключа, или итерация по элементам и так далее.

Операции со словарями и их временная сложность

Здесь мы считаем, что ключ используется для получения, установки или удаления элемента.

Получение элемента: O(1).
Установка элемента: O(1).
Удаление элемента: O(1).
Проход по словарю: O(n).