Создаем генератор текста на основе цепей Маркова: теория и практика

Рассказывает Александр Деджу, студент Make School’s Product College

Эта статья дает общее представление о том, как генерировать тексты при помощи моделирования марковских процессов. В частности, мы познакомимся с цепями Маркова, а в качестве практики реализуем небольшой генератор текста на Python.

Для начала выпишем нужные, но пока не очень понятные нам определения со страницы в Википедии, чтобы хотя бы примерно представлять, с чем мы имеем дело:

Марковский процесс — случайный процесс, эволюция которого после любого заданного значения временного параметра t не зависит от эволюции, предшествовавшей t, при условии, что значение процесса в этот момент фиксировано.

Марковская цепь — частный случай марковского процесса, когда пространство его состояний дискретно (т.е. не более чем счетно).

Что все это значит? Давайте разбираться.

Основы

Первый пример предельно прост. Используя предложение из детской книжки, мы освоим базовую концепцию цепи Маркова, а также определим, что такое в нашем контексте корпус, звенья, распределение вероятностей и гистограммы. Несмотря на то, что предложение приведено на английском языке, суть теории будет легко уловить.

Это предложение и есть корпус, то есть база, на основе которой в дальнейшем будет генерироваться текст. Оно состоит из восьми слов, но при этом уникальных слов только пять — это звенья (мы ведь говорим о марковской цепи). Для наглядности окрасим каждое звено в свой цвет:

И выпишем количество появлений каждого из звеньев в тексте:

На картинке выше видно, что слово «fish» появляется в тексте в 4 раза чаще, чем каждое из других слов («One», «two», «red», «blue»). То есть вероятность встретить в нашем корпусе слово «fish» в 4 раза выше, чем вероятность встретить каждое другое слово из приведенных на рисунке. Говоря на языке математики, мы можем определить закон распределения случайной величины и вычислить, с какой вероятностью одно из слов появится в тексте после текущего. Вероятность считается так: нужно разделить число появлений нужного нам слова в корпусе на общее число всех слов в нем. Для слова «fish» эта вероятность — 50%, так как оно появляется 4 раза в предложении из 8 слов. Для каждого из остальных звеньев эта вероятность равна 12,5% (1/8).

Графически представить распределение случайных величин можно с помощью гистограммы. В данном случае, наглядно видна частота появления каждого из звеньев в предложении:

Итак, наш текст состоит из слов и уникальных звеньев, а распределение вероятностей появления каждого из звеньев в предложении мы отобразили на гистограмме. Если вам кажется, что возиться со статистикой не стоит, прочитайте наш перевод, который вас переубедит. И, возможно, сохранит вам жизнь.

Суть определения

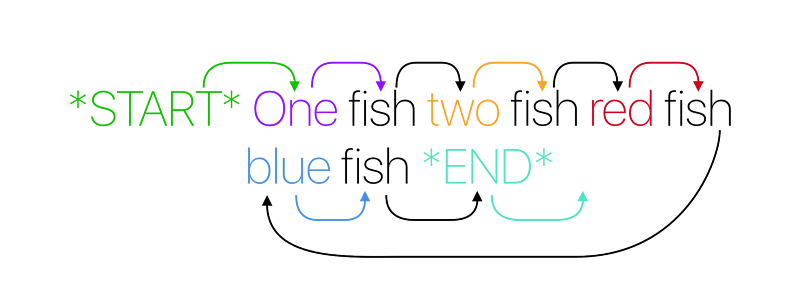
Теперь добавим к нашему тексту элементы, которые всегда подразумеваются, но не озвучиваются в повседневной речи — начало и конец предложения:

Любое предложение содержит эти невидимые «начало» и «конец», добавим их в качестве звеньев к нашему распределению:

Вернемся к определению, данному в начале статьи:

Марковский процесс — случайный процесс, эволюция которого после любого заданного значения временного параметра t не зависит от эволюции, предшествовавшей t, при условии, что значение процесса в этот момент фиксировано.

Марковская цепь — частный случай марковского процесса, когда пространство его состояний дискретно (т.е. не более чем счетно).

Так что же это значит? Грубо говоря, мы моделируем процесс, в котором состояние системы в следующий момент времени зависит только от её состояния в текущий момент, и никак не зависит от всех предыдущих состояний.

Представьте, что перед вами окно, которое отображает только текущее состояние системы (в нашем случае, это одно слово), и вам нужно определить, каким будет следующее слово, основываясь только на данных, представленных в этом окне. В нашем корпусе слова следуют одно за другим по такой схеме:

Таким образом, формируются пары слов (даже у конца предложения есть своя пара — пустое значение):

Сгруппируем эти пары по первому слову. Мы увидим, что у каждого слова есть свой набор звеньев, которые в контексте нашего предложения могут за ним следовать:

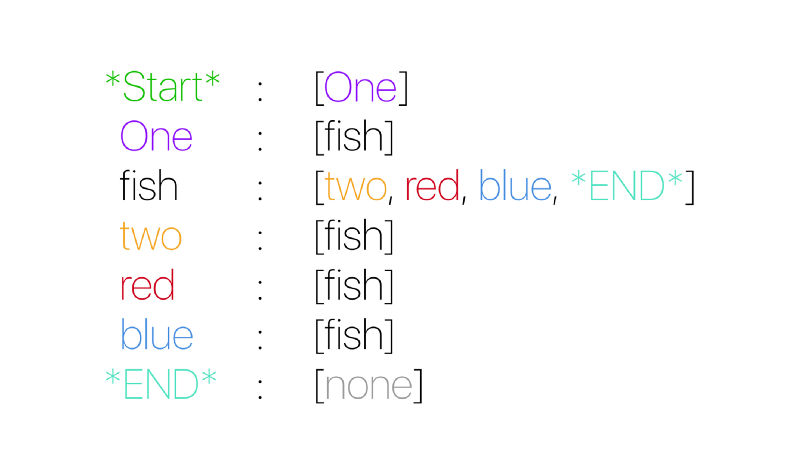
Представим эту информацию другим способом — каждому звену поставим в соответствие массив из всех слов, которые могут появиться в тексте после этого звена:

Разберем подробнее. Мы видим, что у каждого звена есть слова, которые могут стоять после него в предложении. Если бы мы показали схему выше кому-то еще, этот человек с некоторой вероятностью мог бы реконструировать наше начальное предложение, то есть корпус.

Пример. Начнем со слова «Start». Далее выбираем слово «One», так как по нашей схеме это единственное слово, которое может следовать за началом предложения. За словом «One» тоже может следовать только одно слово — «fish». Теперь новое предложение в промежуточном варианте выглядит как «One fish». Дальше ситуация усложняется — за «fish» могут с равной вероятностью в 25% идти слова «two», «red», «blue» и конец предложения «End». Если мы предположим, что следующее слово — «two», реконструкция продолжится. Но мы можем выбрать и звено «End». В таком случае на основе нашей схемы будет случайно сгенерировано предложение, сильно отличающееся от корпуса — «One fish».

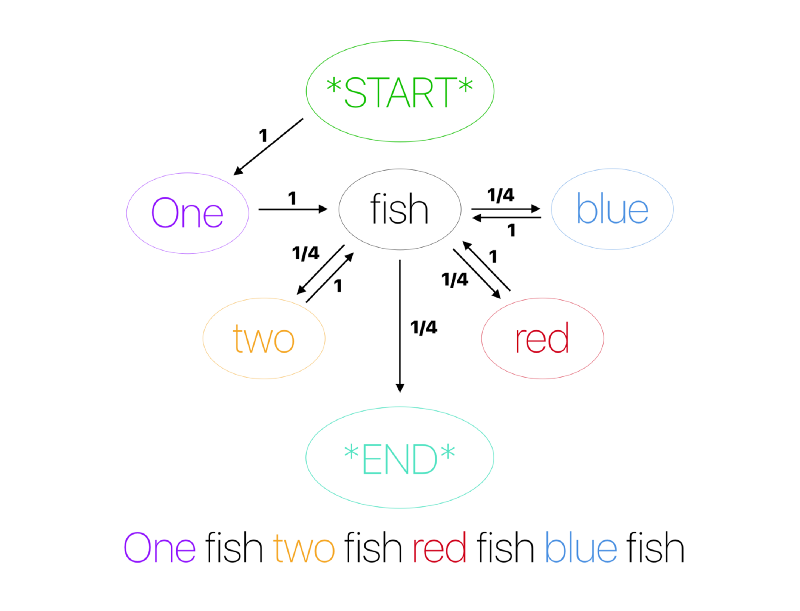
Мы только что смоделировали марковский процесс — определили каждое следующее слово только на основании знаний о текущем. Давайте для полного усвоения материала построим диаграммы, отображающие зависимости между элементами внутри нашего корпуса. Овалы представляют собой звенья. Стрелки ведут к потенциальным звеньям, которые могут идти за словом в овале. Около каждой стрелки — вероятность, с которой следующее звено появится после текущего:

Отлично! Мы усвоили необходимую информацию, чтобы двигаться дальше и разбирать более сложные модели.

Расширяем словарную базу

В этой части статьи мы будем строить модель по тому же принципу, что и раньше, но при описании опустим некоторые шаги. Если возникнут затруднения, возвращайтесь к теории в первом блоке.

Возьмем еще четыре цитаты того же автора (также на английском, нам это не помешает):

«Today you are you. That is truer than true. There is no one alive who is you-er than you.»

«You have brains in your head. You have feet in your shoes. You can steer yourself any direction you choose. You’re on your own.»

«The more that you read, the more things you will know. The more that you learn, the more places you’ll go.»

«Think left and think right and think low and think high. Oh, the thinks you can think up if only you try.»

Сложность корпуса увеличилась, но в нашем случае это только плюс — теперь генератор текста сможет выдавать более осмысленные предложения. Дело в том, что в любом языке есть слова, которые встречаются в речи чаще, чем другие (например, предлог «в» мы используем гораздо чаще, чем слово «криогенный»). Чем больше слов в нашем корпусе (а значит, и зависимостей между ними), тем больше у генератора информации о том, какое слово вероятнее всего должно появиться в тексте после текущего.

Проще всего это объясняется с точки зрения программы. Мы знаем, что для каждого звена существует набор слов, которые могут за ним следовать. А также, каждое слово характеризуется числом его появлений в тексте. Нам нужно каким-то образом зафиксировать всю эту информацию в одном месте; для этой цели лучше всего подойдет словарь, хранящий пары «(ключ, значение)». В ключе словаря будет записано текущее состояние системы, то есть одно из звеньев корпуса (например, «the» на картинке ниже); а в значении словаря будет храниться еще один словарь. Во вложенном словаре ключами будут слова, которые могут идти в тексте после текущего звена корпуса («thinks» и «more» могут идти в тексте после «the»), а значениями — число появлений этих слов в тексте после нашего звена (слово «thinks» появляется в тексте после слова «the» 1 раз, слово «more» после слова «the» — 4 раза):

Перечитайте абзац выше несколько раз, чтобы точно разобраться. Обратите внимание, что вложенный словарь в данном случае — это та же гистограмма, он помогает нам отслеживать звенья и частоту их появления в тексте относительно других слов. Надо заметить, что даже такая словарная база очень мала для надлежащей генерации текстов на естественном языке — она должна содержать более 20 000 слов, а лучше более 100 000. А еще лучше — более 500 000. Но давайте рассмотрим ту словарную базу, которая получилась у нас.

Цепь Маркова в данном случае строится аналогично первому примеру — каждое следующее слово выбирается только на основании знаний о текущем слове, все остальные слова не учитываются. Но благодаря хранению в словаре данных о том, какие слова появляются чаще других, мы можем при выборе принять взвешенное решение. Давайте разберем конкретный пример:

То есть если текущим словом является слово «more», после него могут с равной вероятностью в 25% идти слова «things» и «places», и с вероятностью 50% — слово «that». Но вероятности могут быть и все равны между собой:

Работа с окнами

До настоящего момента мы с вами рассматривали только окна размером в одно слово. Можно увеличить размер окна, чтобы генератор текста выдавал более «выверенные» предложения. Это значит, что чем больше окно, тем меньше будет отклонений от корпуса при генерации. Увеличение размера окна соответствует переходу цепи Маркова к более высокому порядку. Ранее мы строили цепь первого порядка, для окна из двух слов получится цепь второго порядка, из трех — третьего, и так далее.

Окно — это те данные в текущем состоянии системы, которые используются для принятия решений. Если мы совместим большое окно и маленький набор данных, то, скорее всего, каждый раз будем получать одно и то же предложение. Давайте возьмем словарную базу из нашего первого примера и расширим окно до размера 2:

Расширение привело к тому, что у каждого окна теперь только один вариант следующего состояния системы — что бы мы ни делали, мы всегда будем получать одно и то же предложение, идентичное нашему корпусу. Поэтому, чтобы экспериментировать с окнами, и чтобы генератор текста возвращал уникальный контент, запаситесь словарной базой от 500 000 слов.

Реализация на Python

Структура данных Dictogram

Dictogram (dict — встроенный тип данных словарь в Python) будет отображать зависимость между звеньями и их частотой появления в тексте, то есть их распределение. Но при этом она будет обладать нужным нам свойством словаря — время выполнения программы не будет зависеть от объема входных данных, а это значит, мы создаем эффективный алгоритм.

			import random

class Dictogram(dict):
    def __init__(self, iterable=None):
        # Инициализируем наше распределение как новый объект класса, 
        # добавляем имеющиеся элементы
        super(Dictogram, self).__init__()
        self.types = 0  # число уникальных ключей в распределении
        self.tokens = 0  # общее количество всех слов в распределении
        if iterable:
            self.update(iterable)

    def update(self, iterable):
        # Обновляем распределение элементами из имеющегося 
        # итерируемого набора данных
        for item in iterable:
            if item in self:
                self[item] += 1
                self.tokens += 1
            else:
                self[item] = 1
                self.types += 1
                self.tokens += 1

    def count(self, item):
        # Возвращаем значение счетчика элемента, или 0
        if item in self:
            return self[item]
        return 0

    def return_random_word(self):
        random_key = random.sample(self, 1)
        # Другой способ:
        # random.choice(histogram.keys())
        return random_key[0]

    def return_weighted_random_word(self):
        # Сгенерировать псевдослучайное число между 0 и (n-1),
        # где n - общее число слов
        random_int = random.randint(0, self.tokens-1)
        index = 0
        list_of_keys = self.keys()
        # вывести 'случайный индекс:', random_int
        for i in range(0, self.types):
            index += self[list_of_keys[i]]
            # вывести индекс
            if(index > random_int):
                # вывести list_of_keys[i]
                return list_of_keys[i]
		

В конструктор структуре Dictogram можно передать любой объект, по которому можно итерироваться. Элементами этого объекта будут слова для инициализации Dictogram, например, все слова из какой-нибудь книги. В данном случае мы ведем подсчет элементов, чтобы для обращения к какому-либо из них не нужно было пробегать каждый раз по всему набору данных.

Мы также сделали две функции для возврата случайного слова. Одна функция выбирает случайный ключ в словаре, а другая, принимая во внимание число появлений каждого слова в тексте, возвращает нужное нам слово.

Структура цепи Маркова

			from histograms import Dictogram

def make_markov_model(data):
    markov_model = dict()

    for i in range(0, len(data)-1):
        if data[i] in markov_model:
            # Просто присоединяем к уже существующему распределению
            markov_model[data[i]].update([data[i+1]])
        else:
            markov_model[data[i]] = Dictogram([data[i+1]])
    return markov_model
		

В реализации выше у нас есть словарь, который хранит окна в качестве ключа в паре «(ключ, значение)» и распределения в качестве значений в этой паре.

Структура цепи Маркова N-го порядка

			from histograms import Dictogram


def make_higher_order_markov_model(order, data):
    markov_model = dict()

    for i in range(0, len(data)-order):
        # Создаем окно
        window = tuple(data[i: i+order])
        # Добавляем в словарь
        if window in markov_model:
            # Присоединяем к уже существующему распределению
            markov_model[window].update([data[i+order]])
        else:
            markov_model[window] = Dictogram([data[i+order]])
    return markov_model
		

Очень похоже на цепь Маркова первого порядка, но в данном случае мы храним кортеж в качестве ключа в паре «(ключ, значение)» в словаре. Мы используем его вместо списка, так как кортеж защищен от любых изменений, а для нас это важно — ведь ключи в словаре меняться не должны.

Парсинг модели

Отлично, мы реализовали словарь. Но как теперь совершить генерацию контента, основываясь на текущем состоянии и шаге к следующему состоянию? Пройдемся по нашей модели:

			from histograms import Dictogram
import random
from collections import deque
import re


def generate_random_start(model):
    # Чтобы сгенерировать любое начальное слово, раскомментируйте строку:
    # return random.choice(model.keys())

    # Чтобы сгенерировать "правильное" начальное слово, используйте код ниже:
    # Правильные начальные слова - это те, что являлись началом предложений в корпусе
    if 'END' in model:
        seed_word = 'END'
        while seed_word == 'END':
            seed_word = model['END'].return_weighted_random_word()
        return seed_word
    return random.choice(model.keys())


def generate_random_sentence(length, markov_model):
    current_word = generate_random_start(markov_model)
    sentence = [current_word]
    for i in range(0, length):
        current_dictogram = markov_model[current_word]
        random_weighted_word = current_dictogram.return_weighted_random_word()
        current_word = random_weighted_word
        sentence.append(current_word)
    sentence[0] = sentence[0].capitalize()
    return ' '.join(sentence) + '.'
    return sentence
		

Лучше генерировать «правильные» начальные слова – те, которые и в исходном тексте стояли в начале предложения. Для этого мы в словаре находим все ключи «END» и выбираем слово, следующее за одним из них. После генерации начального слова мы ищем, какое слово может идти дальше, обращаясь к тому же словарю, и выбираем нужное на основании комбинации вероятности и случайности. Продолжаем это делать, пока предложение не достигнет установленной нами длины, и в конце возвращаем его. Если вам интересно больше узнать о парсинге, посмотрите наш перевод про историю синтаксического анализа.

Что дальше?

Попробуйте придумать, где вы сами можете использовать генератор текста на основе марковских цепей. Только не забывайте, что самое главное – это то, как вы парсите модель и какие особые ограничения устанавливаете на генерацию. Автор этой статьи, например, при создании генератора твитов использовал большое окно, ограничил генерируемый контент до 140 символов и использовал для начала предложений только «правильные» слова, то есть те, которые являлись началом предложений в корпусе.

Вы также можете продолжить дальше изучать марковские процессы и, например, попробовать разобраться в том, что такое скрытые марковские модели.