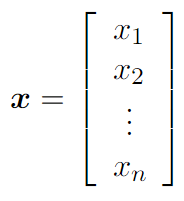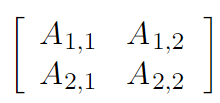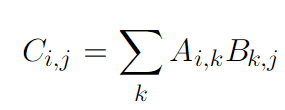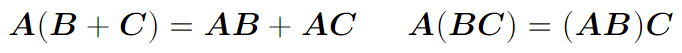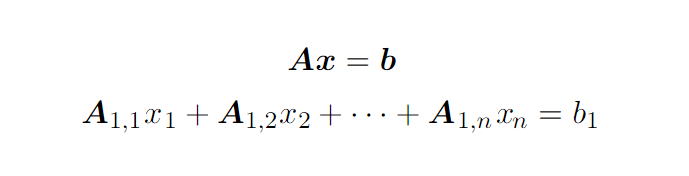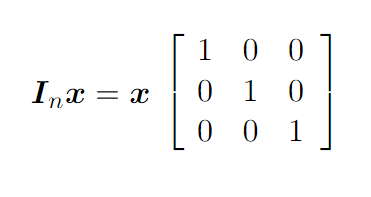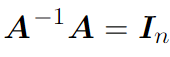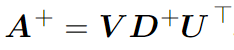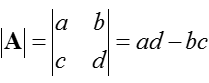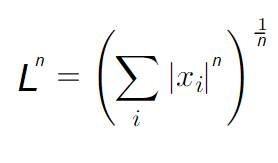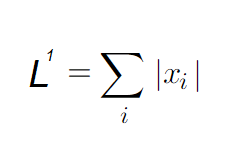Математика для ИИ: линейная алгебра

В мире IT сейчас часто можно услышать о машинном обучении, нейронных сетях и искусственном интеллекте. И не удивительно — эти отрасли быстро развиваются и используются для решения различного рода задач.

Большинство концепций были открыты ещё 50 лет назад, и множество из них основаны на математических принципах. Поэтому у людей, пытающихся войти в данную нишу, часто возникает вопрос: «На каком уровне нужно знать математику?». Эта статья даст представление о некоторых необходимых основах, в частности, о базовых концепциях линейной алгебры.

Базовые термины

По сути, вся линейная алгебра вертится вокруг нескольких понятий: векторы, скаляры, тензоры и матрицы, — всё это очень важно для машинного обучения, ведь благодаря им можно абстрагировать данные и модели. Например, каждая запись в каком-нибудь наборе данных может быть представлена в виде вектора в многомерном пространстве, а параметры нейронных сетей абстрагируются как матрицы. Каждое из понятий по своему специфично, так что рассмотрим их подробнее.

Скаляр

Скаляр — это просто число, в отличие от вектора или матрицы. Скаляры определены как элементы поля, предназначенные для описания пространства вектора. Несколько скаляров образуют вектор. Скаляры могут быть представлены разными типами чисел: вещественными, действительными или натуральными. Обозначаются скаляры строчными и прописными буквами латинского и греческого алфавита:

Вектор

Вектор — это упорядоченный массив скаляров. Скаляры выступают в роли координат точек в пространстве. Скопление векторов становится так называемым векторным пространством. Векторы можно складывать вместе, перемножать друг на друга и масштабировать. Они обозначаются жирным шрифтом. Каждый элемент вектора имеет индекс.

Матрица

Матрица — это двумерный массив скаляров. Обозначается жирным шрифтом в верхнем регистре. Например, если говорить о матрице из вещественных чисел, где m рядов и n столбцов, записывается такая матрица вот так:Поскольку матрица — двумерный массив, элементы матрицы имеют два индекса:Две матрицы могут быть сложены или вычтены одна из другой, только если у матриц одинаковое количество рядов и столбцов. Две матрицы могут быть перемножены только тогда, когда количество столбцов первой матрицы соответствует количеству рядов второй. Например, вы можете умножить матрицу A размера m, n на матрицу B размера n, p. В результате вы получите матрицу C размера m, p. Формула умножения выглядит вот так:

Важно заметить, что матричное произведение дистрибутивно и ассоциативно:

Однако, иногда может понадобиться перемножить элементы матриц между собой. Такую операцию называют произведением Адамара (обозначается  A ∘ B). Матрицы также можно умножать на векторы и на скаляры. Интересно, что произведением матрицы и вектора будет вектор:

Тензор

Тензор — это многомерный массив чисел. Обычно в нём больше двух измерений, так что он может быть изображён как многомерная сетка, состоящая из чисел. На самом деле, матрицы — те же тензоры, только они двухмерные, вот и все их отличия. Тензоры получили известность благодаря фреймворку для машинного обучения TensorFlow.

Операции

Есть несколько операций, которые можно производить с матрицами, и знание которых пригодится для понимания принципов работы ИИ.

Транспонирование матрицы

В результате выполнения этой операции появляется так называемая транспонированная матрица. По сути, это зеркальное отображение матрицы по главной диагональной линии, которая начинается в верхнем левом и идёт в правый нижний угол. Транспонированной матрицей от матрицы A будет матрица AT (также A′, Atr, tA или At). Кроме того, транспонированную матрицу можно получить, записав ряды матрицы A как столбцы матрицы AT, а столбцы матрицы A — как ряды матрицы AT.

Умножение единичной матрицы на вектор

Существует такое понятие как единичная матрица. Если умножить её на вектор, значения вектора не меняются. Элементы главной диагонали единичной матрицы имеют значение 1, а все остальные равны 0:

Перед тем, как вы продолжите, немного информации о диагональной матрице (она очень похожа на единичную). Все элементы матрицы, за исключением тех, что находятся на главной диагонали, равны нулю. Но, в отличие от единичной, на главной диагонали диагональной матрицы элементы имеют значение, не равное 1. Получается, единичная матрица — это вид диагональной матрицы. Они очень полезны для некоторых алгоритмов.

Умножение на обратную матрицу

Обратная матрица определяется следующим образом:

Если умножить матрицу A на обратную ей матрицу A-1, получится единичная матрица. Обратная матрица похожа на обратное число. То есть для a обратным числом будет 1/a. Если обычное число умножить на обратное ему, получится единица: a * 1/a = 1. Здесь то же самое, только с матрицами. Но, увы, это работает только с квадратными матрицами.

Псевдоинверсия Мура-Пенроуза

Для неквадратных матриц нужно применять псевдоинверсию Мура-Пенроуза:Где U, D и V — сингулярное разложение матрицы A. Псевдоинверсия D+ матрицы D создаётся путём взятия элементов, обратных элементам матрицы, и её дальнейшим транспонированием. Но будьте осторожны с концепцией обратной матрицы A-1, потому что пока что она больше используется в теории, чем на практике. Это обусловлено тем, что вычислительные способности современных компьютеров позволяют дать лишь приблизительный ответ.

Преобразование матрицы в скаляр

Бывает, что нужно преобразовать матрицу в скаляр, для этого нужно найти определитель, он обозначается det(A) или |A|. Так как преобразование возможно только с ними, вот пример с матрицей 2×2:Напоследок про линейную зависимость. Набор векторов будет линейно зависим, если хотя бы один вектор может быть представлен как комбинация других векторов из набора. Иначе набор будет линейно независим. Обычно векторы x и y будут линейно независимы, только если значения для скаляров a и b, удовлетворяющих ax + by = 0, будут равны a = b = 0.

Нормы

Иногда для работы с вектором нужно знать его размер. Для этого существуют специальные функции, которые называют нормами — Ln. Маленькая буква n обозначает количество измерений, в которых находится вектор. В зависимости от того, сколько измерений в вашем векторном пространстве, нормы будут разными. Наиболее известная норма — норма двумерного пространства (Евклидова норма). Чаще всего она представляет собой Евклидово расстояние от начала вектора до точки в пространстве, находящейся на конце этого вектора. При обобщении пространства на несколько измерений используют глобальную норму:На самом деле, нормой может быть любая функция, удовлетворяющая следующим требованиям:

1. f(x + y) ≤ f(x) + f(yv) (удовлетворяет неравенству треугольника).
2. f(ax) = |a| f(x) (является абсолютно масштабируемой).
3. Если f(x) = 0, то x = 0 (определена положительно).

Часто, когда вы создаёте ИИ-приложение, очень важно различать элементы, равные 0, и элементы, имеющие значение, близкое к 0. Для этого используется норма L1. Она проста и растёт с одинаковой скоростью во всех точках векторного пространства. Если любой элемент вектора x движется от 0 к a — эта функция вырастает на a:Как упоминалось выше, в глубоком обучении параметры нейронных сетей абстрагируются как матрицы. Следовательно, нужно знать размер матрицы, и с этим нам поможет норма Фробениуса:

Заключение

В этой статье мы затронули основы линейной алгебры, которые пригодятся, чтобы понять, что же происходит в мире нейронных сетей и искусственного интеллекта. Надеемся, эта статья поможет вам начать свой путь в этой сфере. Успехов!