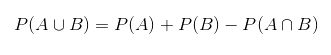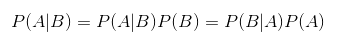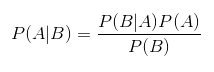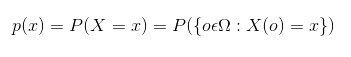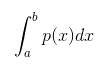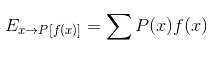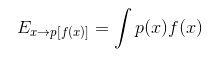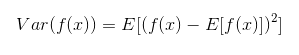Математика для ИИ: теория вероятностей

Машинное обучение, глубокое обучение и ИИ — интересные и широко обсуждаемые темы по всему миру. Но как и в разработке ПО, разобраться в этой области сможет не каждый. Многие думают, что если у них за плечами годы разработки различных приложений, то они имеют преимущество над простыми новичками. В какой-то степени они правы, но «не говори гоп, пока не перепрыгнешь», особенно когда дело касается математики.

В предыдущей статье вы познакомились с базовыми концепциями линейной алгебры. Эта статья поведает вам о теории вероятностей. Учитывайте, что цель статьи — не заменить курс в университете, а познакомить читателя с темой, чтобы дальше он уже сам решил, стоит ли ему углубляться.

Базовые термины

Может быть немного странно работать с вероятностями в информатике, так как большинство ветвей имеют дело с детерминированными и определёнными сущностями. Но когда речь идёт об искусственном интеллекте, неопределённость и хаотичность проявляется во многих формах. Безусловно, данные являются основным источником неопределённости, но источником может быть и модель. И теория вероятностей обеспечивает методы для моделирования и работы с неопределённостью, её используют для анализа частоты возникновения событий.

Вероятность — возможность осуществления чего-либо. По сути, это число от 0 до 1, где 0 указывает на невозможность возникновения события, а 1 указывает на достоверность его возникновения. Вероятность возникновения события A будет обозначаться  P(A) или p(A). То есть, если P(A) = 1, то можно сказать, что событие A точно произойдёт, а если P(A) = 0, то событие точно не произойдёт. В связи с этим, можно вывести P(Ac), дополнение события. Оно имеет значение P(Ac) = 1 – P(A) и обозначает вероятность того, что событие A никогда не произойдёт.

Когда речь идёт о вероятностях нескольких событий и взаимодействиях между ними, используется термин совместная вероятность. Она представляет собой вероятность того, что произойдут оба события. Если эти события независимы, совместную вероятность можно определить так:

Однако, если эти события являются взаимоисключающими, формула усложняется:Теперь будут приведены некоторые термины, которые используются при вычислении вероятности. Какова вероятность события A, если произошло событие B? Для того, чтобы узнать, нужно вычислить условную вероятность.

Очень интересно, что совместная вероятность по нескольким случайным переменным может быть разделена на условные распределения по одной переменной — такое преобразование называют цепным правилом:Также следует упомянуть простое, но основополагающее правило Байеса. Оно описывает вероятность события, базируясь на знании условий или других событий, связанных с главным событием:Или же его упорядоченная версия:
P(A) — априорная вероятность гипотезы A, P(A|B) – вероятность гипотезы A при наступлении события B (апостериорная вероятность), а P(B|A) – вероятность наступления события B при истинности гипотезы A. Когда мы говорим о машинном обучении, глубоком обучении или искусственном интеллекте, мы используем правило Байеса для обновления параметров нашей модели.

Случайные величины и распределение вероятностей

Случайной величиной называется такая величина, которая случайно принимает какое-то значение из множества возможных значений. Или более точно — это функция, которая конвертирует результат какого-либо изменяющегося процесса в числовое значение. В математике обозначается так:

Здесь Ω — это набор возможных исходов, а Е — некоторое измеримое пространство. Однако, случайная величина — лишь шаблон, она содержит возможные значения процесса. И чтобы она стала по-настоящему полезной, её стоит объединить с распределением вероятностей. В итоге вы узнаете, насколько вероятно каждое значение. Случайные величины могут быть как дискретными, так и непрерывными, и как следствие, существуют два способа описания распределения вероятностей.

Дискретная случайная величина имеет конечное число значений. Их можно рассматривать в качестве категориальных переменных или перечислений. Распределение вероятностей по этому типу случайных величин описывается с помощью функции вероятностной массы (англ. probability mass function — PMF). Эта функция определяет вероятность  того, что дискретная случайная величина равняется тому или иному значению. Предполагается, что Х: Ω → [0, 1] — это дискретная случайная величина, содержащая набор возможных исходов Ω для пространства со значениями 0 и 1:

Непрерывная случайная величина имеет значения из множества действительных чисел (а их бесконечное множество). Распределение вероятностей случайной величины этого типа определяется при помощи функции плотности вероятности (англ. probability density function — PDF). Эта функция должна чётко соответствовать условиям: во-первых, область р — это набор всех возможных значений х. Стоит уточнить: функция принимает только значения больше или равные 0. Во-вторых, функция должна удовлетворять следующему условию:

Но проблема в том, что эта функция не определяет вероятность конкретного значения, а даёт вероятность нахождения этого значения в бесконечно малой области значений. И всё потому, что вероятность того, что распределение вероятности примет какое-либо конкретное значение, равна 0, так как существует бесконечное множество возможных значений. Вероятность того, что х находится где-то в промежутке [a, b], определяется так:

Математическое ожидание, дисперсия и ковариация

В теории вероятностей математическое ожидание определяется как среднее значение повторения некоторого события. То есть ожидаемое значение некоторой функции f(x) над распределением вероятностей P(x) является средним значением f, когда x берётся из P. Для дискретных случайных величин оно определяется следующим образом:

А для непрерывных случайных величин вот так:

Можно сказать, что данное значение является мерой так называемого «центра» распределения вероятностей. Но также хотелось бы узнать, как меняются значения функции f(x) случайной величины x, когда мы берём разные значения из её распределения вероятностей P(x). Это называется дисперсией. Она представляет собой среднеквадратическое отклонение значений f(x) от среднего значения f(x):

А корень этого выражения будет называться стандартным отклонением. Исходя из этого можно определить ковариацию. По сути, это мера линейной зависимости двух случайных величин. Она показывает, насколько сильно два числа линейно связаны: