Оптимизация алгоритмов оптимизации

Один из способов решить сложную проблему оптимизации — сначала свести её к соответствующей, но более простой задаче, а затем постепенно увеличивать сложность, каждый раз решая новую проблему, и, в свою очередь, используя это решение в качестве руководства к решению последующей задачи. Такой подход, кажется, довольно хорошо работает на практике, но он никогда не был описан и подтвержден теоретически.

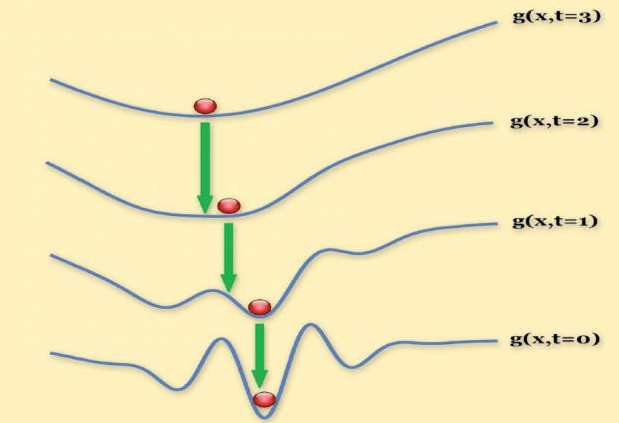
Эта последовательность графиков иллюстрирует применение метода исследователей к реальной проблеме компьютерного зрения. Решение каждой задачи (красные шарики) используется для инициализации (зеленые стрелки) поиска решения в последующей.

В январе на Международной конференции по методам геометрической оптимизации в компьютерном зрении и распознавании образов, Хоссейн Мобэхи (Hossein Mobahi), учёный, проводящий докторские исследования в Массачусетском технологическом институте информатики и лаборатории искусственного интеллекта (Computer Science and Artificial Intelligence Laboratory — CSAIL), и Джон Фишер (John Fisher), старший научный сотрудник в CSAIL, описали способ генерации последовательности упрощенных функций, что гарантирует наилучшее приближение у применяемого в настоящее время метода.

«На некоторые фундаментальные вопросы об этом методе мы отвечаем впервые», — говорит Мобэхи. — «Например, я сказал вам, что надо начинать с простой задачи, но не сказал, как выбрать эту простую задачу. Существует бесконечно много функций, с которых вы можете начать. Какая из них лучше? Даже если я скажу вам с какой функции стоит начать, есть бесконечно много способов её преобразования для определенной задачи. И это преобразование влияет на то, что вы получите в конце».

Достижение минимума

Чтобы понять, как работает оптимизация, предположим, что вы ритейлер консервированных продуктов. Вы пытаетесь сэкономить деньги на стали и хотите, чтобы соотношение площади поверхности банки к её объёму сводилось к минимуму. Это соотношение является функцией от высоты и радиуса, так что если вы сможете найти минимальное значение функции, то будете знать оптимальные размеры банки. Если вы дизайнер автомобилей, который старается сбалансировать затраты на компоненты, изготовленные из различных материалов, с весом и аэродинамическим сопротивлением автомобиля, ваша функция — известная в оптимизации как «функция затрат» — будет намного сложнее, но принцип останется все тем же.

Алгоритмы машинного обучения часто пытаются выявить особенности наборов данных, что полезно для задач классификации — скажем, визуальные черты, характерные для автомобилей. Поиск наименьшего такого набора функций с наибольшей прогностической ценностью также является проблемой оптимизации.

«Большинство эффективных алгоритмов, которые применяются в настоящее время для решения задач оптимизации, работают на основе локального поиска. При этом на начальном этапе вам необходимо задать им какое-либо значение, являющееся предполагаемым решением. Далее алгоритмы определяют в каком направлении стоит двигаться, чтобы улучшить его, а затем осуществляют этот шаг», — говорит Мобэхи. — «Используя эту технику, они могут сходиться к значению под названием ‘локальный минимум’, который является точкой, которая в сравнении с соседними, лежащими в окрестности, находится ниже. Но найденное решение не будет являться глобальным минимумом: может существовать, которая находится намного ниже, но дальше».

Однако локальный минимум гарантированно будет глобальным, если функция — выпуклая вниз. Функция f(x) = x2 выпуклая, так как описывает параболу с центром в начале координат. Функция f(x) = sin х — нет, так как описывает синусоиду, которая колеблется вверх и вниз.

Сглаживание

Метод Мобэхи и Фишера пытается найти выпуклую аппроксимацию задачи оптимизации, используя технику, называемую сглаживание (фильтром) Гаусса. Сглаживание Гаусса преобразует функцию затрат в зависимую функцию, которая дает не значение, описывающее функцию стоимости, а взвешенное среднее всех ближайших значений. Это позволяет сглаживать резкие спады или подъемы на графике функции затрат.

Веса, присвоенные близлежащим значениям, определяются функцией Гаусса или нормальным распределением — колоколообразной кривой, знакомой из статистики. Близлежащие значения рассчитываются преимущественно по средним, а не отдаленным значениям.

Ширина гауссовой функции определяется одним параметром. Мобэхи и Фишер начали с очень широкого гауссиана (Gaussian), который при определенных условиях дает выпуклую функцию. Затем они постепенно уменьшали ширину гауссиана, создавая серию промежуточных задач. На каждом этапе они используют решение последней задачи для инициализации поиска решения последующей. К тому времени, когда ширина распределения сократилась до нуля, они восстановили первоначальную функцию затрат, так как каждое значение представляло собой просто среднее значение.

«Метод продолжения оптимизации на самом деле широко используется в практике, в компьютерном зрении, для решения проблемы выравнивания, отслеживания и во многих других задачах, но сам он не очень понятный», — говорит Джон Райт (John Wright), доцент кафедры электротехники в Колумбийском университете. — «Самое интересное в работе Хоссейна в целом, и этой статье, в частности, в том, что он действительно копается в этом методе и пытается узнать, что можно сказать о нем с точки зрения аналитики».

«Практическая польза состоит в том, что может быть любое число различных способов, которыми вы могли бы пойти при выполнении сглаживания или попытке осуществить «грубо-точную» оптимизацию», — добавляет Райт. — «Но если вы заранее знаете о правильном пути, то вам не нужно тратить много времени на неверные методы. У вас уже есть рецепт, так зачем искать что-то иное?»

Перевод статьи «Optimizing optimization algorithms: Getting best results when approximating solutions to complex engineering problems»