Основные концепции статистики для data scientist’ов

Статистика — мощный инструмент в Data Science. Она позволяет извлечь информацию из данных, узнать их структуру и на основе полученной информации провести дальнейший анализ. В этой статье будет рассмотрено 5 базовых концепций статистики, которые следует знать data scientist’ам.

Статистические характеристики

Статистические характеристики — наверное, наиболее часто используемая статистическая концепция в Data Science. Обычно это первое, что применяют при исследовании набора данных. В эту концепцию входят такие понятия как отклонение, дисперсия, среднее значение, медиана, процентили и многие другие. Их довольно легко понять и реализовать в коде:

Линия посередине — это медианное значение данных. Медиану используют вместо среднего значения по той причине, что она более устойчива к аномальным значениям в данных. Первый квартиль — это 25 процентиль, т.е. 25% значений в данных находятся ниже этого значения. Третий квартиль — это 75 процентиль, т.е. 75% значений в данных находятся ниже этого значения. Минимальное и максимальное значения отражают нижнюю и верхнюю границы диапазона данных.

Ящик с усами прекрасно демонстрирует, что мы можем сделать с основными статистическими характеристиками:

• Когда этот ящик короткий, то можно сделать вывод, что большинство значений в данных похожи, так как много значений находится на небольшом расстоянии друг от друга.
• Когда ящик длинный, то можно сделать обратный вывод: большинство значений отличаются друг от друга.
• Если медианное значение ближе к низу, то можно сказать, что большая часть данных имеет более низкие значения. Если оно ближе к верху, то большая часть данных имеет более высокие значения. По сути, если медиана не находится по центру ящика, то это показатель того, что данные неравномерны.
• Усы очень длинные? Значит, данные имеют высокое стандартное отклонение и дисперсию, т.е. значения сильно разбросаны и отличаются друг от друга. Если усы длинные только с одной стороны ящика, то, возможно, данные заметно изменяются только в одном направлении.

Используйте статистические характеристики для быстрой, но при этом информативной оценки ваших данных.

Распределения вероятностей

Вероятность можно определить как процентный шанс того, что какое-то событие произойдёт. В Data Science вероятность находится в пределах от 0 до 1, где 0 означает, что событие точно не произойдёт, а 1 — что точно произойдёт. Распределение вероятностей — это функция, которая отображает вероятности всех возможных значений. Рассмотрим основные виды распределений.

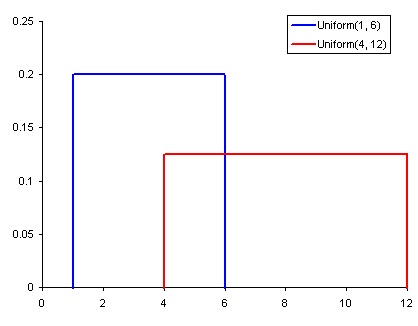
Равномерное распределение — самое базовое из представленных здесь. У него есть единственное значение, которое встречается только в определённом диапазоне, а всё, что находится за его пределами, равно нулю. Это распределение можно воспринимать как признак категориальной переменной с двумя категориями: 0 и значением. У такой переменной могут быть и другие значения, отличные от нуля, но это не мешает изобразить её в виде функции, состоящей из нескольких равномерных распределений.

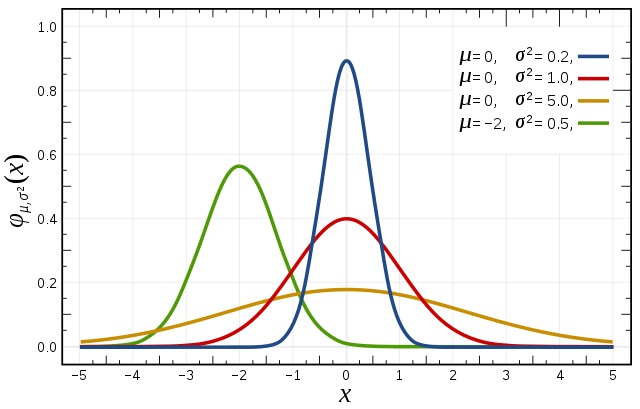
Нормальное распределение или распределение Гаусса определяется медианой и стандартным отклонением. Медиана сдвигает распределение в пространстве, а отклонение влияет на масштаб. Важное отличие этого распределения от других заключается в том, что стандартное отклонение одинаково во всех направлениях. Таким образом, с распределением Гаусса чётко видно среднее значение в наборе данных. Также становится наглядным распределение данных, т.е. распределены ли они на большом промежутке или же сконцентрированы вокруг нескольких значений.

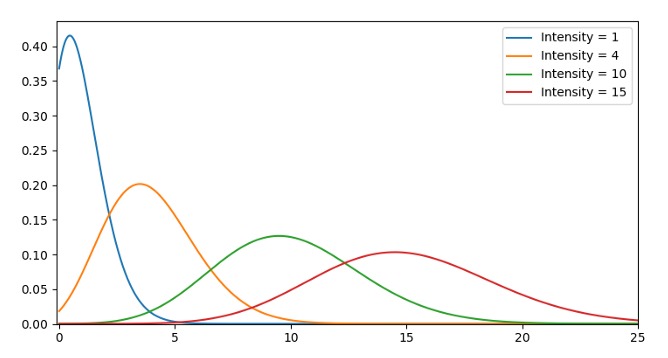
Распределение Пуассона похоже на нормальное, но с дополнительным коэффициентом асимметрии. При низком коэффициенте значения распределены относительно равномерно во все стороны, как при нормальном распределении. Если же он высокий, то распределение данных будет разным в разных направлениях — в одном данные будут сильно распределены, а в другом — сильно сконцентрированы.

Существует гораздо больше распределений, но этих трёх достаточно для понимания основ. С помощью равномерного распределения можно быстро рассмотреть и интерпретировать категориальные переменные. При нормальном распределении существует много алгоритмов, которые по умолчанию хорошо работают с этим распределением. При распределении Пуассона нужно внимательно подойти к выбору алгоритма, потому что он должен быть устойчив к изменениям в пространственном распределении.

Снижение размерности

Этот термин легко понять интуитивно. Есть набор данных и нужно уменьшить количество его измерений. В Data Science под этим подразумевается количество переменных признаков:

Куб представляет набор данных, имеет три измерения и содержит 1000 точек. Конечно, при современных вычислительных мощностях таким количеством никого не напугать, но когда это число начнёт расти, могут появиться проблемы. Однако, если посмотреть на данные с двухмерной точки зрения, можно увидеть, что с такого угла легко разделить все цвета. С помощью снижения размерности можно спроецировать 3D-данные на 2D-плоскость, что эффективно снижает количество точек для вычисления до 100 единиц.

Снизить размерность также можно с помощью отбрасывания маловажных признаков. Например, после изучения набора данных было выявлено, что из 10 признаков 7 сильно коррелируют с выходом, а остальные 3 — нет. Значит, 3 этих признака не стоят траты ресурсов на них и их можно исключить без вреда для выхода.

Наиболее распространённый метод для снижения размерности — метод главных компонент (PCA), который создаёт векторные представления признаков, тем самым показывая их связь с выходом. PCA можно использовать для обоих вариантов снижения размерности, описанных выше.

Оверсемплинг и андерсемплинг

Оверсемплинг и андерсемплинг используются в задачах классификации. Порой набор данных для классификации сильно сдвинут в одну сторону. Например, для класса 1 может быть 2000 примеров, а для класса 2 — всего 200. Это негативно повлияет на многие методы машинного обучения, которые используются для моделирования данных и составления предсказаний. Овер- и андерсемплинг нужны как раз для таких случаев:

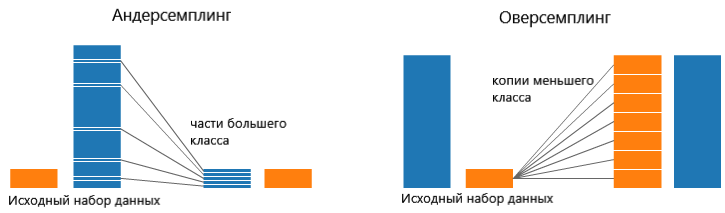
На обеих сторонах этой картинки синий класс содержит гораздо больше данных, чем оранжевый. В такой ситуации можно предпринять один из двух шагов для препроцессинга данных перед их использованием для обучения моделей.

Андерсемплинг означает, что используется только часть данных большего класса. Это необходимо для поддержания распределения вероятности класса.

Оверсемплинг означает, что создаются копии меньшего класса, чтобы сравнять его размер с большим классом. Копии делаются таким образом, чтобы поддерживать распределение меньшего класса.

Статистика Байеса

Чтобы понять предназначение статистики Байеса, нужно сначала разобраться, что не так с частотной статистикой. Большинство людей думает именно о частотной статистике, когда слышит слово «статистика». В этой статистике используется математика для анализа вероятности того, что какое-то событие произойдёт, а вычисления происходят только на основе априорных данных.

Рассмотрим пример. Предположим, человеку дали шестигранный кубик и спросили, какова вероятность выпадения 6. Большинство людей сразу скажут, что шанс равен 1/6. И действительно, если провести частотный анализ и посмотреть на данные, полученные после 10 тысяч бросков, то можно увидеть, что шанс выпадения каждого числа примерно равен 1/6.

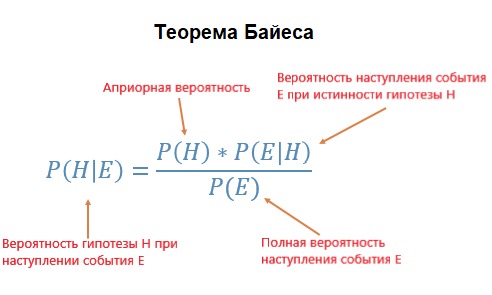
Но что, если кто-то скажет, что это шулерский кубик, который всегда приземляется на 6? Так как частотный анализ учитывает только априорные данные, это утверждение не будет принято во внимание. А в случае со статистикой Байеса — будет:

Вероятность P(H) в уравнении — это частотный анализ, который учитывает априорные данные для подсчёта вероятности какого-то события. P(E|H) — вероятность того, что событие E произойдёт при истинности выдвинутого предположения. Например, если бросить кубик 10000 раз и за первую тысячу бросков выпадут только шестёрки, то явно можно заподозрить, что предположение верное. P(E) — вероятность того, что предположение является истинным.

Как можно увидеть из формулы, статистика Байеса всё принимает во внимание: частотный анализ,  вероятность того, что предположение о шулерском кубике верно и вероятность выпадения 6, если оно верно. Её целесообразно применять, когда нет уверенности, что априорные данные будут не очень хорошо отображать будущие данные и результаты.

Смотрите также: Основы статистики с Python: описательная статистика