Как написать бота, которого будет нельзя обыграть в «крестики-нолики», или Знакомство с правилом «минимакс»

Вполне возможно, что после сотен партий в «крестики-нолики» вы задумывались: каков же оптимальный алгоритм? Но если вы здесь, то вы наверняка ещё и пробовали написать реализацию этой игры. Мы пойдём дальше и напишем бота, который будет невозможно обыграть в «крестики-нолики». Предугадав ваш вопрос «почему?», ответим: благодаря алгоритму «минимакс».

Как и профессиональный шахматист, этот алгоритм просчитывает действия соперника на несколько ходов вперёд — до тех пор, пока не достигнет конца партии, будь то победа, поражение или ничья. Попав в это конечное состояние, ИИ начислит себе положительное количество очков (в нашем случае +10) за победу, отрицательное (-10) — за поражение, и нейтральное (0) — за ничью.

В то же время алгоритм проводит аналогичные расчёты для ходов игрока. Он будет выбирать ход с наиболее высоким баллом, если ходит ИИ, и ход с наименьшим, если ходит игрок. Используя такую стратегию, минимакс избегает поражения.

Попробуйте сыграть вот в такую игру. 

Алгоритм «минимакс» проще всего описать в виде рекурсивной функции, которая:

1. возвращает значение, если найдено конечное состояние (+10, 0, -10),
2. проходит по всем пустым клеткам на поле,
3. вызывает минимакс-функцию для каждой из них (рекурсия),
4. оценивает полученные значения
5. и возвращает наилучшее из них.

Если вы не знакомы с рекурсией, то вам стоит посмотреть эту лекцию из гарвардского курса CS50:

Чтобы разобраться в том, как устроен минимакс, давайте напишем его реализацию и смоделируем его поведение. Займёмся этим в двух следующих разделах.

Реализация минимакса

Мы рассмотрим ситуацию, когда игра подходит к концу (смотрите картинку ниже). Поскольку минимакс проходит по всем возможным состояниям игры (а их сотни тысяч), имеет смысл рассматривать эндшпиль — так нам придётся отслеживать меньшее количество рекурсивных вызовов функции (всего 9).

Пусть ИИ играет крестиками, человек — ноликами.

Чтобы упростить работу с полем, объявим его как массив из 9 элементов со значениями, равными содержимому клеток. Заполним его крестиками и ноликами, как на картинке выше, и назовём origBoard.

			var origBoard = ["O",1,"X","X",4,"X",6,"O","O"];
		

Затем объявим переменные aiPlayer и huPlayer и присвоим им значения "X" и "O" соответственно.

Кроме того, нам потребуется функция, которая ищет победные комбинации и возвращает истинное значение в случае успешного поиска, и функция, которая хранит индексы доступных клеток.

			/* начальное состояние доски
  O |   | X
  ---------
  X |   | X
  ---------
    | O | O
  */
var origBoard = [“O”,1 ,”X”,”X”,4 ,”X”, 6 ,”O”,”O”];

// человек
var huPlayer = “O”;

// ИИ
var aiPlayer = “X”;

// возвращает список индексов пустых клеток доски
function emptyIndices(board){
  return  board.filter(s => s != "O" && s != "X");
}

// победные комбинации с учётом индексов
function winning(board, player){
  if(
    (board[0] == player && board[1] == player && board[2] == player) ||
    (board[3] == player && board[4] == player && board[5] == player) ||
    (board[6] == player && board[7] == player && board[8] == player) ||
    (board[0] == player && board[3] == player && board[6] == player) ||
    (board[1] == player && board[4] == player && board[7] == player) ||
    (board[2] == player && board[5] == player && board[8] == player) ||
    (board[0] == player && board[4] == player && board[8] == player) ||
    (board[2] == player && board[4] == player && board[6] == player)
    ) {
      return true;
      } else {
      return false;
      }
}
		

Итак, давайте определим минимакс-функцию с двумя аргументами: newBoard (новое поле) и player (игрок). Затем найдём индексы свободных клеток на поле и передадим их в переменную availSpots.

			// основная минимакс-функция
function minimax(newBoard, player){
  
  //доступные клетки
  var availSpots = emptyIndices(newBoard);
		

Кроме того, нам нужно отслеживать конечные состояния и возвращать соответствующие значения. Если побеждает «нолик», нужно вернуть -10, если «крестик» — +10. Если размер массива availSpots равен нулю, значит, свободных клеток нет, игра закончится ничьёй, и нужно вернуть ноль.

			// проверка на терминальное состояние (победа / поражение / ничья)
  //and returning a value accordingly
  if (winning(newBoard, huPlayer)){
    return {score:-10};
  }
  else if (winning(newBoard, aiPlayer)){
    return {score:10};
  }
  else if (availSpots.length === 0){
    return {score:0};
  }
		

После этого нужно собрать очки с каждой из пустых клеток. Для этого создадим массив ходов moves и пройдём в цикле по всем пустым клеткам, помещая индексы и очки каждого хода в объект move.

Затем зададим индекс пустой клетки, который хранился в виде числа в origBoard, равным свойству-индексу объекта move. Потом сходим за текущего игрока на пустую клетку нового поля newBoard и вызовем функцию minimax от другого игрока и получившегося поля newBoard. После этого нужно поместить свойство score объекта, возвращённого функцией minimax, в свойство score объекта move.

Если минимакс не находит конечное состояние, он продолжает рекурсивное углубление в ход игры до тех пор, пока не достигнет терминального состояния. После этого он передаёт очки этого «уровня» рекурсии на один уровень выше.

И наконец, функция сбрасывает изменения newBoard и помещает объект move в массив moves.

			// массив для хранения всех объектов
  var moves = [];

  // цикл по доступным клеткам
  for (var i = 0; i < availSpots.length; i++){
    //create an object for each and store the index of that spot 
    var move = {};
  	move.index = newBoard[availSpots[i]];

    // совершить ход за текущего игрока
    newBoard[availSpots[i]] = player;

    //получить очки, заработанные после вызова минимакса от противника текущего игрока
    if (player == aiPlayer){
      var result = minimax(newBoard, huPlayer);
      move.score = result.score;
    }
    else{
      var result = minimax(newBoard, aiPlayer);
      move.score = result.score;
    }

    // очистить клетку
    newBoard[availSpots[i]] = move.index;

    // положить объект в массив
    moves.push(move);
  }
		

Затем минимаксу нужно выбрать наилучший ход move из массива moves. Ему нужен move с наибольшим счётом, если ходит ИИ, и с наименьшим, если это ход человека. Таким образом, если значение player равно aiPlayer, алгоритм инициализирует переменную bestScore очень маленьким числом и идёт циклом по массиву moves: если ход move приносит больше очков score, чем bestScore, алгоритм запоминает этот move. В случае ходов с одинаковыми очками алгоритм запоминает первый из них.

В случае, когда player равен huPlayer, всё аналогично — только теперь bestScore инициализируется большим числом, а минимакс ищет ход move с наименьшим количеством очков.

В итоге минимакс возвращает объект, хранящийся в bestMove.

			// если это ход ИИ, пройти циклом по ходам и выбрать ход с наибольшим количеством очков
  var bestMove;
  if(player === aiPlayer){
    var bestScore = -10000;
    for(var i = 0; i < moves.length; i++){
      if(moves[i].score > bestScore){
        bestScore = moves[i].score;
        bestMove = i;
      }
    }
  }else{

// иначе пройти циклом по ходам и выбрать ход с наименьшим количеством очков
    var bestScore = 10000;
    for(var i = 0; i < moves.length; i++){
      if(moves[i].score < bestScore){
        bestScore = moves[i].score;
        bestMove = i;
      }
    }
  }

// вернуть выбранный ход (объект) из массива ходов
  return moves[bestMove];
}
		

Вот и вся минимакс-функция. Исходный код реализации алгоритма вы можете найти на GitHub и CodePen.

В следующем разделе мы смоделируем работу нашей программы, чтобы понять, как она работает.

Минимакс в действии

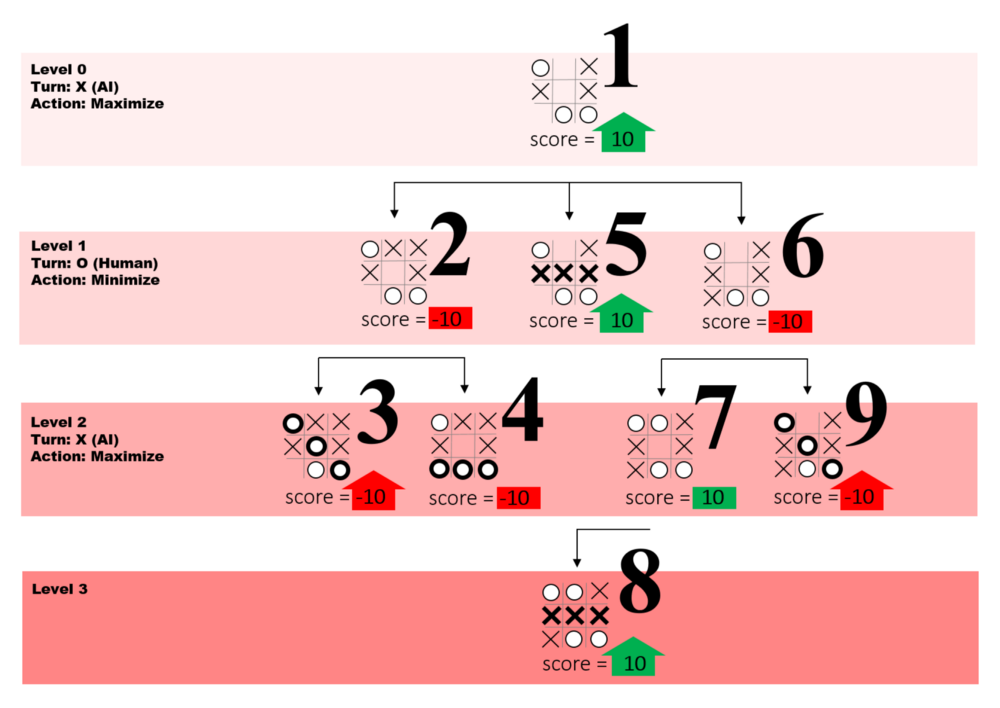
Пользуясь схемой ниже, разберем пошаговую модель алгоритма.

Примечание: На схеме большие числа обозначают порядковый номер вызова функции, а уровни — то, на сколько ходов вперёд прошёл алгоритм.

1. Алгоритму подаются origBoard и aiPlayer. Он составляет список из трёх найденных пустых клеток, проверяет конечность состояния, и проходит циклом по всем пустым клеткам. Затем алгоритм меняет newBoard, помещая aiPlayer в первую пустую клетку. После этого он вызывает сам себя от newBoard и huPlayer и ждёт, пока второй вызов вернёт значение.
2. Пока первый вызов функции всё ещё работает, запускается второй, создавая список из двух пустых клеток, проверяя конечность состояния и проходя циклом по всем пустым клеткам. Затем второй вызов изменяет newBoard, помещая huPlayer в первую пустую клетку. После этого он вызывает сам себя от newBoard и aiPlayer и ждёт, пока третий вызов вернёт значение.
3. Алгоритм составляет список пустых клеток и фиксирует победу игрока после проверки конечности состояния. Поэтому он возвращает объект с полем счёта, равным (-10).
   Поскольку второй вызов обнаружил две пустые клетки, минимакс изменяет newBoard, помещая huPlayer во вторую свободную клетку. Затем он вызывает сам себя от newBoard и aiPlayer.
4. Алгоритм составляет список пустых клеток и фиксирует победу игрока после проверки конечности состояния. Поэтому он возвращает объект с полем счёта, равным (-10).
   Во втором вызове функции алгоритм получает значения, возвращённые с нижнего уровня третьим и четвёртым вызовами функции. Поскольку ход huPlayer принёс эти два результата, алгоритм выбирает наименьший из них. Так как они одинаковы, алгоритм выбирает первый и передаёт его первому вызову функции.На этот момент первый вызов функции получил оценку хода aiPlayer в первую пустую клетку. Затем он изменяет newBoard, помещая aiPlayer во вторую пустую клетку. После этого он вызывает сам себя от newBoard и huPlayer.
5. В пятом вызове функции алгоритм составляет список пустых клеток и фиксирует победу ИИ после проверки конечности состояния. Поэтому он возвращает объект с полем счёта, равным +10.
   После этого первый вызов изменяет newBoard, помещая aiPlayer в третью пустую клетку. Затем он вызывает сам себя от newBoard и huPlayer.
6. Шестой вызов  составляет список из двух пустых клеток, проверяет конечность состояния и идёт циклом по всем пустым клеткам. Затем он изменяет newBoard, помещая huPlayer в первую пустую клетку. Потом он вызывает сам себя от newBoard и aiPlayer и ждёт, пока седьмой вызов вернёт значение.
7. Новый вызов составляет список из одной пустой клетки, проверяет конечность состояния и изменяет newBoard, помещая aiPlayer в пустую клетку. После этого он вызывает сам себя от newBoard и huPlayer и ждёт, пока этот вызов вернёт значение.
8. Восьмой вызов составляет пустой список пустых клеток и фиксирует победу aiPlayer после проверки конечности состояния. Поэтому он возвращает объект с полем счёта, равным (+10), на уровень выше, седьмому вызову.
   Седьмой вызов получил лишь одно, положительное значение от нижних уровней. Поскольку это значение было получено в ход aiPlayer, алгоритм возвращает наибольшее из полученных значений. Поэтому он возвращает положительное значение (+10) на уровень выше, шестому вызову.Поскольку шестой вызов обнаружил две пустых клетки, минимакс изменяет newBoard, помещая huPlayer во вторую пустую клетку. Затем он вызывает сам себя от newBoard и aiPlayer.
9. После этого алгоритм составляет список пустых клеток и фиксирует победу aiPlayer после проверки конечности состояния. Поэтому он возвращает объект с полем счёта, равным (+10), на уровень выше.
   На этом этапе шестой вызов должен выбрать между счётом (+10), который вернул седьмой вызов, и счётом (-10), который вернул девятый вызов. Поскольку ход huPlayer принёс эти два результата, алгоритм выбирает наименьший из них и возвращает его на уровень выше в виде объекта с полями счёта и индекса.Наконец, все три ветви первого вызова оцениваются (-10, +10, -10). Поскольку ход aiPlayer принёс эти три результата, алгоритм выбирает объект, содержащий наибольшее количество очков (+10) и его индекс (4).

В рассмотренном выше сценарии минимакс решает, что оптимальным выбором будет ход в центральную клетку поля.

Выводы

К этому моменту вы должны были понять, как устроен алгоритм минимакс. Попробуйте написать его реализацию самостоятельно или посмотрите пример на GitHub или CodePen и оптимизируйте его.

Если вас заинтересовала тема ИИ в играх, советуем почитать наши материалы по этой теме:

• Серия статей, посвящённая написанию ИИ для хоккея.
• Как создать лучшего бота для игры в стиле Dota — интервью с победителем соревнования Russian AI Cup.