Большой сборник завораживающих визуализаций известных алгоритмов

Возможности человеческого разума ограничены […] Наша сила — в использовании технологий, которые многократно увеличивают наши когнитивные способности — Дональд Норман

Алгоритмы — это отличная область применения визуализации. Для визуализации работы алгоритма не нужны реальные данные. Это позволяет разработчикам экспериментировать с различными формами представления информации и делает алгоритмы отличным предметом для изучения с помощью визуализации.

Кроме того, это напоминание, что визуализация — нечто большее, чем просто инструмент для нахождения закономерностей в данных. Визуализация помогает человеку лучше воспринимать зрительную информацию: мы можем использовать ее для понимания абстрактных процессов, и не только их.

Прим. пер.: Это текстовый вариант выступления автора на фестивале Eyeo 2014. Видеозапись выступления доступна на Vimeo.

Семплинг

Прежде, чем приступить к объяснению первого алгоритма, следует описать задачу, которую он должен решать.

«Звездная ночь», Ван Гог

Свет — электромагнитное излучение. Свет, испускаемый монитором, проходит через окружающий воздух, фокусируется вашим хрусталиком и попадает на сетчатку. Это непрерывный сигнал. Однако, для того, чтобы его воспринять, наш глаз должен разложить его на дискретные имульсы, измеряя интенсивность и распределение частоты в различных точках.

Этот процесс называется «дискретизация» или «семплинг» (sampling) (прим. перев.: далее в статье, будет использоваться калька с англ., поскольку оригинальный термин имеет более широкое значение), и он является основой нашего зрения. Представьте художника, который кладет дискретные мазки на холст, чтобы сформировать изображение (в частности направление Пуантилизма). Семплинг — основа компьютерной графики. К примеру, для растеризации трехмерной сцены с освещением мы долны решить, как будут проецироваться лучи света. Даже простое изменение размера изображения использует семплинг.

При выполнении семплинга мы сталкиваемся с двумя проблемами. С одной стороны, точки долны быть распределены равномерно, без пустот. С другой — необходимо избежать повторяющихся паттернов, которые вызывают алиасинг. Именно по этой причине не стоит носить рубашку в мелкую полоску, когда вы попадаете в камеру. Полоски резонируют с сеткой пикселей на матрице камеры и вызывают муаровый узор.

Микрофотография сетчатки

Сетчатка человека — это отличный пример правильного расположения рецепторов. На фотографии видны колбочки — более крупные клетки, которые отвечают за восприятие цвета, и более мелкие палочки — они отвечают за зрение в условиях низкой освещенности. Клетки распределены по поверхности плотно и равномерно (за исключением слепого пятна около зрительного нерва), но в случайном порядке. Такое распределение называется «дисковым распределением Пуассона», оно обеспечивает минимальное расстояние между клетками, избегая при этом наложения их друг на друга.

К сожалению, генерация распределения Пуассона трудна в реализации (об этом немного позже). Поэтому рассмотрим простое приближение в виде алгоритма Митчелла для поиска наилучшего кандидата.

(function() {

var margin = 3, width = 720 - margin - margin, height = 270 - margin - margin;

var numSamplesPerFrame = 10, numSamples = 2000, numCandidates = 10, timerActive = 0;

var p = d3.select("#best-candidate-sampling") .on("click", click);

var svg = p.append("svg") .attr("width", width + margin + margin) .attr("height", height + margin + margin) .append("g") .attr("transform", "translate(" + margin + "," + margin + ")");

p.append("button") .text("▶ Play");

whenFullyVisible(p.node(), click);

function click() { var sample = bestCandidateSampler(width, height, numCandidates, numSamples), timer = ++timerActive;

svg.selectAll("circle").remove(); p.classed("animation--playing", true);

d3.timer(function() { if (timerActive !== timer) return true; for (var i = 0; i

Как вы можете видеть, поиск наилучшего кандидата дает вполне равномерное распределение, хотя и не без недочетов. В некоторых областях точек слишком много, в некотрых — слишком мало. Но результат вполне допустимый и, что главное, легко реализуемый.

Вот как он работает:

(function() {

var width = 720, height = 500;

var numCandidates = 10, numSamplesMax = 1000;

var p = d3.select("#best-candidate-explainer") .on("click", click);

var svg = p.append("svg") .attr("width", width) .attr("height", height);

var gCandidate = svg.append("g") .attr("class", "candidate");

var gPoint = svg.append("g") .attr("class", "point");

p.append("button") .text("▶ Play");

beforeVisible(p.node(), click);

function click() { var numSamples = 1;

var quadtree = d3.geom.quadtree() .extent([[0, 0], [width, height]]) ([[Math.random() * width, Math.random() * height]]);

gCandidate.selectAll("*") .interrupt() .remove();

gPoint.selectAll("*") .interrupt() .remove();

gPoint.append("circle") .attr("r", 3.5) .attr("cx", quadtree.point[0]) .attr("cy", quadtree.point[1]);

p.classed("animation--playing", true);

(function nextPoint() { var i = 0, maxDistance = -Infinity, bestCandidate = null;

(function nextCandidate() { if (++i > numCandidates) { gCandidate.selectAll("*").transition() .style("opacity", 0) .remove();

gPoint.append("circle") .attr("r", 3.5) .attr("cx", bestCandidate.__data__[0]) .attr("cy", bestCandidate.__data__[1]);

quadtree.add(bestCandidate.__data__);

if (++numSamples maxDistance) { d3.select(bestCandidate).attr("class", null); d3.select(this.parentNode.appendChild(this)).attr("class", "candidate--best"); bestCandidate = this; maxDistance = distance; } else { d3.select(this).attr("class", null); } nextCandidate(); });

t.select("circle.search") .attr("r", distance);

t.select("line.search") .attr("x2", closest[0]) .attr("y2", closest[1]); })(); })();}

})()

На каждой итерации алгоритм генерирует фиксированное количество кандидатов из равномерного распределения, показаных серым цветом. В данном случае их 10.

Наилучший кандидат, показаный красным — тот, который находится дальше всего от каждой точки с предыдущей итерации. Они отмечены черным цветом. Расстояние от каждого кандидата до ближайшей точки показано с помощью окружности с кандидатом в центре и радиальной линии. Заметьте, что внутри любой красной или серой окружности нет черных точек. После того, как созданы все кандидаты и измерены все расстояния, наилучший кандидат становится новой точкой, а другие кандидаты отбрасываются.

Вот код, который реализует этот алгоритм:

Поскольку я объяснил работу алгоритма выше, я оставлю код без комментариев. (Все-таки цель этой статьи — визуализация). Однако я уточню некоторые детали:

Внешняя переменная numCandidates определяет количество кандидатов, генерируемых на каждой итерации. Изменение этого параметра позволяет регулировать соотношение скорости и качества генерации. Чем меньше количество кандидатов, тем быстрее работает алгоритм, но качество генерации при этом падает.

Функция distance — простая геометрия:

Примечание: Можно убрать отсюда вычисление квадратного корня, так как поскольку функция без перегибов, на определение найлучшего кандидата это не повлияет.

Функция findClosest возвращает ближайшую к кандидату точку. Это можно сделать простым перебором или быстрее, например, используя quadtree. Перебор просто реализовать, но работает он медленно, за квадратичное время. Второй вариант заметно быстрее, но требует больше усилий для реализации.

Говоря о компромиссах: при принятии решения об использовании того или иного алгоритма мы рассматриваем его в сравнении с другими вариантами. На одной чаше весов находится сложность реализации и поддержки, на другой — качество и скорость работы.

Самая простая альтернатива — использовать равномерное распределение:

Результат выглядит так:

(function() {

var margin = 3, width = 720 - margin - margin, height = 360 - margin - margin;

var numSamplesPerFrame = 10, numSamples = 2000, timerActive = 0;

var p = d3.select("#uniform-random-sampling") .on("click", click);

var svg = p.append("svg") .attr("width", width + margin + margin) .attr("height", height + margin + margin) .append("g") .attr("transform", "translate(" + margin + "," + margin + ")");

p.append("button") .text("▶ Play");

whenFullyVisible(p.node(), click);

function click() { var sample = uniformRandomSampler(width, height, numSamples), timer = ++timerActive;

svg.selectAll("circle").remove(); p.classed("animation--playing", true);

d3.timer(function() { if (timerActive !== timer) return true; for (var i = 0; i

Ужасно, не правда ли? Мы можем наблюдать как участки с очень малой плотностью, так и с очень большой. В некоторых местах точки даже накладываются друг на друга. Некоторые области совсем пустые. Равномерное распределение также показывает нам нижнюю границу качества для алгоритма поиска наилучшего кандидата, когда количество генерируемых кандидатов равно единице.

Распределение точек — один из вариантов оценки качества семплинга, но не единственный. К примеру, мы можем попытаться сэмулировать зрение с различными стратегиями семплинга, раскрашивая изображение в цвет ближайшей точки. По сути, мы получим диаграмму Вороного тех участков, где каждая ячейка выкрашена в соответствующий цвет.

Вот так выглядит «Звездная ночь» через 6667 равномерно распределенных точек:

«Звездная ночь» через равномерно распределенные ячейки

Очевидно, что качество оставляет желать лучшего. Ячейки сильно варьируются по размеру, как и следовало ожидать. Некоторые детали потерялись из-за плотно расположенных ячеек. Кроме того, в тех местах, где точки расположены редко (большие ячейки), аггрегируются редкие цвета, как, например, розовая звезда слева внизу.

Теперь посмотрим на алгоритм поиска наилучшего кандидата:

«Звездная ночь» через ячейки, сгенерированные по алгоритму поиска наилучшего кандидата

Намного лучше! Ячейки теперь имеют более-менее постоянный размер и при этом случайно расположены. Несмотря на то, что количество точек осталось тем же (6667), изображение сохранило существенно больше деталей и имеет меньше шумов. Если присмотреться, можно даже различить отдельные мазки.

Мы можем использовать диаграммы Вороного для изучения распределения точек напрямую, раскрашивая область по-разному, в зависимости от ее площади. Чем реже расположены точки, тем больше площадь, тем темнее области. Более светлые участки — более плотно расположенные точки. Оптимальное распределение даст почти однородное заполнение при сохранении случайного расположения. (Гистограмма, показывающая распределение площади ячеек тоже информативна, но диаграмма Вороного одновременно показывает еще и расположение точек.)

Вот те же 6667 точек из равномерного распределения:

Диаграмма Вороного для равномерного распределения

Черные пятна — большие промежутки между точками — это области с меньшей детализацией. Такое же количество точек, но распределенных по другому алгоритму, дает более равномерное распределение и, следовательно, более однородный цвет:

Диаграмма Вороного для ячеек, сгенерированных по алгоритму поиска наилучшего кандидата

Можем ли мы сделать еще лучше? Да! Причем, мы не только получим лучший результат, но и получим его быстрее — за линейное время. Кроме того, этот алгоритм почти также просто реализовать, как и поиск наилучшего кандитата, и он прекрасно масштабируется.

Этот замечательный алгоритм — алгоритм Бридсона для распределения Пуассона:

(function() {

var margin = 3, width = 720 - margin - margin, height = 360 - margin - margin;

var numSamplesPerFrame = 10, sampleRadius = 10.29, timerActive = 0;

var p = d3.select("#poisson-disc-sampling") .on("click", click);

var svg = p.append("svg") .attr("width", width + margin + margin) .attr("height", height + margin + margin) .append("g") .attr("transform", "translate(" + margin + "," + margin + ")");

p.append("button") .text("▶ Play");

whenFullyVisible(p.node(), click);

function click() { var sample = poissonDiscSampler(width, height, sampleRadius), timer = ++timerActive;

svg.selectAll("circle").remove(); p.classed("animation--playing", true);

d3.timer(function() { if (timerActive !== timer) return true; for (var i = 0; i

Даже визуально алгоритм работает по-другому: в отличии от первых двух он строит распределение инкрементально, начиная с существующих точек, вместо того, чтобы случайно раскидывать новые. Это делает его похожим, к примеру, на деление клеток в чашке Петри. Заметьте, что новые точки появляются на некотором расстоянии от предыдущих — существует минимальное расстояние, определенное алгоритмом.

А вот как он работает:

(function() {

var width = 720, height = 480;

var duration = 500;

var k = 30, // maximum number of samples before rejection radius = width / Math.SQRT1_2 / 20, // 100, radius2 = radius * radius, R = 3 * radius2, cellSize = radius * Math.SQRT1_2, gridWidth = Math.ceil(width / cellSize), gridHeight = Math.ceil(height / cellSize), grid, queue, queueSize;

var arcEmptyAnnulus = d3.svg.arc() .innerRadius(radius) .outerRadius(radius) .startAngle(0) .endAngle(2 * Math.PI)();

var arcAnnulus = d3.svg.arc() .innerRadius(radius) .outerRadius(radius * 2) .startAngle(0) .endAngle(2 * Math.PI)();

var p = d3.select("#poisson-disc-explainer") .on("click", click);

var svg = p.append("svg") .attr("width", width) .attr("height", height);

var gExclusion = svg.append("g") .attr("class", "exclusion");

svg.append("path") .attr("class", "grid") .attr("transform", "translate(.5,.5)") .attr("d", d3.range(cellSize, width, cellSize) .map(function(x) { return "M" + Math.round(x) + ",0V" + height; }) .join("") + d3.range(cellSize, height, cellSize) .map(function(y) { return "M0," + Math.round(y) + "H" + width; }) .join(""));

var searchAnnulus = svg.append("path") .attr("class", "candidate-annulus");

var gConnection = svg.append("g") .attr("class", "candidate-connection");

var gSample = svg.append("g") .attr("class", "sample");

var gCandidate = svg.append("g") .attr("class", "candidate");

p.append("button") .text("▶ Play");

function far(x, y) { var i = x / cellSize | 0, j = y / cellSize | 0, i0 = Math.max(i - 2, 0), j0 = Math.max(j - 2, 0), i1 = Math.min(i + 3, gridWidth), j1 = Math.min(j + 3, gridHeight);

for (j = j0; j k) return rejectActive();

var a = 2 * Math.PI * Math.random(), r = Math.sqrt(Math.random() * R + radius2), x = s[0] + r * Math.cos(a), y = s[1] + r * Math.sin(a);

// Reject candidates that are outside the allowed extent. if (0 > x || x >= width || 0 > y || y >= height) return generateCandidate();

// If this is an acceptable candidate, create a new sample; // otherwise, generate a new candidate. gCandidate.append("circle") .attr("r", 1e-6) .attr("cx", x) .attr("cy", y) .transition() .duration(duration / 4) .attr("r", 3.75) .each("end", far(x, y) ? acceptCandidate : generateCandidate);

function acceptCandidate() { sample(x, y); nextActive(); } }

function rejectActive() { queue[i] = queue[--queueSize]; queue.length = queueSize;

sampleActive .classed("sample--active", false);

nextActive(); }

function nextActive() { gCandidate.transition() .duration(duration) .style("opacity", 0) .selectAll("circle") .remove();

gConnection.transition() .duration(duration) .style("opacity", 0) .selectAll("line") .remove();

searchAnnulus.transition() .duration(duration) .style("opacity", 0) .each("end", queueSize ? function() { beforeVisible(p.node(), selectActive); } : function() { p.classed("animation--playing", false); }); } })();}

})()

Красным выделены „активные“ точки. На каждой итерации одна из них выбирается с равной вероятностью. Затем случайно генерируется некоторое количество кандидатов (показанных пустыми черными точками) в пределах области от r до 2r, где r — минимально допустимое расстояние между точками.

Кандидаты, находящиеся на расстоянии r от существующих точек, отбрасываются. Эта зона показана серым цветом, расстояние от кандидата до точки обозначено черной линией. Сетка с шагом r/sqrt(2) ускоряет проверку расстояния до существующих точек: каждая клетка может содержать только одну точку, и проверке подлежит ограниченное количество клеток.

Если кандидат принимается, он остается на поле и создается новая партия кандидатов. Если отклоняются все кандидаты, точка помечается как неактивная и меняет свой цвет на черный. Алгоритм заканчивает работу, когда не остается активных точек.

Диаграмма Вороного показывает лучший результат без слишком темных или слишком светлых участков.

Диаграмма Вороного для ячеек, распределенных по Пуассону

Зведная ночь через ячейки, сгенерированные по распределению Пуассона, сохраняет больше деталей и менее зашумленная. Она похожа на римскую мозаику:

«Звездная ночь» через ячейки, распределенные по Пуассону

Теперь, когда мы увидели несколько примеров, давайте подведем небольшой итог: зачем визуализировать алгоритмы?

Развлечение: наблюдение за работой алгоритма поражает воображение. Особенно когда используются случайные числа. Как бы глупо это не звучало, не стоит недооценивать значимость удовольствия! Более того, несмотря на то, что визуализация не раскрывает тонкостей работы алгоритма, она дает глубокое интуитивное понимание.

Обучение: что лучше объясняет работу алгоритма — код или анимация? А что насчет псевдокода — кода, который нельзя скомпилировать? Формальное описание незаменимо в качестве документации, но визуализация отлично подходит для интуитивного понимая принципа работы.

Отладка: если вы когда-нибудь реализовывали алгоритм, основываясь только на формальном описании, вы возможно замечали, насколько это сложно. Возможность видеть, как работает ваш код, может сильно помочь. Визуализация не замена тестам. Но тесты служат для того, чтобы найти ошибку, а не объяснить ее. Визуализация также может раскрыть неожиданное поведение в вашей реализации, даже если результат выглядит корректно. (См. Learnable Programming и Inventing on Principle Виктора Брета.)

Понимание: даже если вы пытаетесь изучить алгоритм сами, визуализация — незаменимый инструмент для глубокого понимания. Один из самых эффективных способов понять новый материал — обучить кого-то, а визуализировать его — все равно что объяснить самому себе. Проще понять алгоритм интуитивно, чем пытаться запомнить код, так как вы наверняка забудете некоторые мелкие, но важные детали.

Перемешивание

Перемешивание — это процесс перераспределения элементов массива в случайном порядке. К примеру, вы перемешиваете колоду карт перед раздачей в покере. Хороший алгоритм перемешивания несмещенный, любой полученный порядок одинаково вероятен.

Алгоритм Фишера-Йетса — отличный пример, он не только несмещенный, но и выполняется за линейное время, использует константную память и легок в реализации.

			function shuffle(array) {
  var n = array.length, t, i;
  while (n) {
    i = Math.random() * n-- | 0; // 0 ≤ i < n
    t = array[n];
    array[n] = array[i];
    array[i] = t;
  }
  return array;
}
		

Ниже приводится визуализация работы этого кода:

(function() {

var n = 120, array = d3.range(n).map(function(d, i) { return {value: d, index: i}; });

var margin = {top: 60, right: 60, bottom: 60, left: 60}, width = 720 - margin.left - margin.right, height = 180 - margin.top - margin.bottom;

var x = d3.scale.ordinal() .domain(d3.range(n)) .rangePoints([0, width]);

var a = d3.scale.linear() .domain([0, n - 1]) .range([-30, 30]);

var p = d3.select("#fisher-yates-shuffle") .on("click", click);

var svg = p.append("svg") .attr("width", width + margin.left + margin.right) .attr("height", height + margin.top + margin.bottom) .append("g") .attr("transform", "translate(" + margin.left + "," + margin.top + ")");

var line = svg.append("g") .selectAll("line") .data(array) .enter().append("line") .attr("class", "line line--inactive") .attr("transform", transform) .attr("y2", -height);

p.append("button") .text("▶ Play");

whenFullyVisible(p.node(), click);

function click() { var swaps = shuffle(array.slice()).reverse(), swapped = array.slice();

p .classed("animation--playing", true);

line .each(function(d, i) { d.index = i; }) .attr("transform", transform) .attr("class", "line") .interrupt();

(function nextTransition() { var swap = swaps.pop(), i = swap[0], j = swap[1], t;

t = swapped[i]; swapped[i] = swapped[j]; swapped[j] = t; swapped[i].index = i; swapped[j].index = j;

d3.selectAll([line[0][swapped[j].value], line[0][swapped[i].value]]) .attr("class", "line line--active") .each(function() { this.parentNode.appendChild(this); }) .transition() .duration(750) .attr("transform", transform) .each("end", function(d, i) { d3.select(this).attr("class", i || swap[0] === swap[1] ? "line line--inactive" : "line"); if (i || swap[0] === swap[1]) { if (swaps.length) nextTransition(); else p.classed("animation--playing", false); } }); })();}

function transform(d) { return "translate(" + x(d.index) + "," + height + ")rotate(" + a(d.value) + ")";}

function shuffle(array) { var swaps = [], m = array.length, t, i;

while (m) { i = Math.floor(Math.random() * m--); t = array[m]; array[m] = array[i]; array[i] = t; swaps.push([m, i]); }

return swaps;}

})()

Для более детального объяснения работы алгоритма см. мою статью.

Каждый отрезок представляет собой число. Маленькие числа наклонены влево, большие — вправо. (Заметьте, что вы можете перемешивать массивы чего угодно, не только чисел, но такое визуальное представление полезно, чтобы оценить порядок элементов. Идеей послужили иллюстрации Роберта Седжвика в книге Algorithms in C )

Алгоритм разделяет массив на две части: правая, перемешанная, выделена черным; левая выделена серым и содержит необработанные элементы. На каждой итерации берется случайный элемент из левой части и переносится в правую. Изначальный порядок элементов не имеет значения, поэтому вместо переноса элементы просто меняются местами. В конце концов, все элементы массива оказываются перемешаны.

Итак, алгоритм Фишера-Йетса — хороший алгоритм. Как же тогда выглядит плохой? Вот, например:

			// НЕ ДЕЛАЙТЕ ЭТОГО!
function shuffle(array) {
  return array.sort(function(a, b) {
    return Math.random() - .5; // ಠ_ಠ
  });
}
		

Здесь мы используем сортировку с произвольным компаратором для перемешивания. Компаратор определяет порядок элементов. Он принимает два элемента массива — a и b и возвращает число меньше нуля, если a меньше b, число больше нуля, если a больше b, или ноль, если они равны. Компаратор вызывается несколько раз при проходе по массиву.

Если вы не укажете компаратор для array.sort, элементы будут упорядочены лексикографически.

В данном случае компаратор возвращает случайное число от -0,5 до +0,5. Мы исходим из предположения, что в данном случае элементы будут переставлены в случайном порядке.

К сожалению, это предположение неверное. Случайное расположение пары элементов друг относительно друга не даст нам в итоге случайного расположения элементов во всем массиве. Компаратор должен удовлетворять свойству транзитивности: если a > b и b > c, то a > c. Наш компаратор возвращает случайное число, а это значит, что поведение array.sort будет неопределенным. Вам может повезти, а может и не повезти.

Насколько плох этот алгоритм? Давайте посмотрим на результат его работы:

(function() {

var n = 120;

var margin = {top: 60, right: 60, bottom: 60, left: 60}, width = 720 - margin.left - margin.right, height = 180 - margin.top - margin.bottom;

var x = d3.scale.ordinal() .domain(d3.range(n)) .rangePoints([0, width]);

var a = d3.scale.linear() .domain([0, n - 1]) .range([-30, 30]);

var p = d3.select("#random-comparator-shuffle") .on("click", click);

var svg = p.append("svg") .attr("width", width + margin.left + margin.right) .attr("height", height + margin.top + margin.bottom) .append("g") .attr("transform", "translate(" + margin.left + "," + margin.top + ")");

var line = svg.append("g") .selectAll("line") .data(d3.range(n)) .enter().append("line") .attr("class", "line line--inactive") .attr("transform", transform) .attr("y2", -height);

p.append("button") .text("▶ Play");

beforeVisible(p.node(), click);

function click() { p .classed("animation--playing", true);

line .data(shuffle(d3.range(n)), function(d) { return d; }) .interrupt() .transition() .attr("transform", transform) .each("end", function(d, i) { if (!i) p.classed("animation--playing", false); });}

function transform(d, i) { return "translate(" + x(i) + "," + height + ")rotate(" + a(d) + ")";}

// DON’T DO THIS!function shuffle(array) { return array.sort(function() { return Math.random() - .5; // ಠ_ಠ });}

})()

Другая проблема с этим алгоритмом — время работы. Он выполняется за O(n*log n), что делает его заметно медленнее, чем алгоритм Фишера-Йетса, который выполняется за линейное время. Но скорость — проблема меньшая, чем предвзятость.

С первого взгляда может показаться, что он работает правильно и выдает хорошо перемешанный результат. Из этого можно заключить, что наш компаратор достаточно хорош, и не придираться к мелочам. Но не стоит доверять своим глазам — то, что кажется человеческому глазу случайным, может оказаться совсем не случайным.

Этот пример также показывает, что визуализация не серебрянная пуля. Мы должны тщательно продумать способ визуализации, который даст ответ на конкретный вопрос: насколько результат неслучаен?

Но прежде, чем это доказать, мы должны определить, в чем состоит неслучайность результата. Одно из возможных определений — вероятность того, что i-ый элемент после перемешивания окажется на j-ом месте. Если алгоритм дает случайный результат, то для каждого элемента вероятность расположения в любом месте одинакова и равна 1/n, где n — количество элементов.

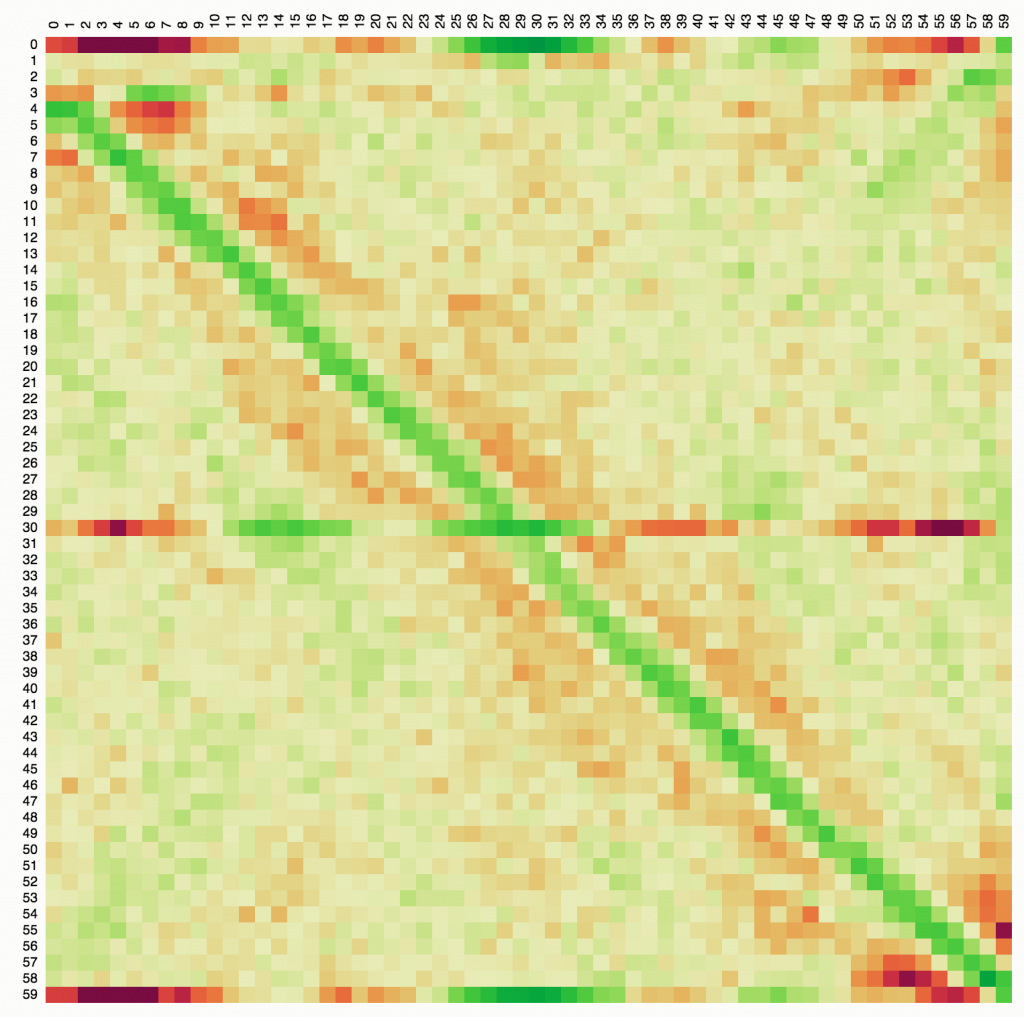
Аналитический расчет этих вероятностей зависит от знания того, какой алгоритм сортировки использовался. Но эмпирически рассчитать их довольно просто: мы перемешиваем массив тысячу раз и считаем количество появлений i-ого элемента на j-ом месте. Результат удобно представить в виде матричной диаграммы:

Столбец (горизонтальное положение ячейки) в матрице показывает индекс элемента до перемешивания, вертикальная позиция — после перемешивания. Вероятность положения точки показана цветом: зеленый — положительное смещение, когда элемент принимает значение чаще, чем мы ожидаем, красный — отрицательное смещение, когда значения возникают реже ожидаемого.

Компаратор на случайных числах в Chrome удивительно неплох. Большая часть массива хорошо перемешана. Однако, мы може видеть положительное смещение ниже диагонали: это говорит нам о том, что алгоритм склонен перемещать элементы с i на i+1 или i+2. Также можно увидеть странное поведение в первом, последнем и среднем рядах, что может быть следствием использования median-of-three quicksort.

Алгоритм Фишера-Йетса выглядит так:

Здесь нет никаких повторяющихся участков, только небольшой шум из-за неточности измерений. (При желании от него можно избавиться, проведя дополнительные замеры.)

Поведение этого компаратора зависит от его реализации в браузере. Разные браузеры используют разные алгоритмы сортировки, а они, в свою очередь, выдают разные (неверные) результаты при использовании компаратора на случайных числах. Вот пример работы перемешивания с таким компаратором в Firefox:

Интерактивную версию этой матрицы для исследования различных алгоритмов перемешивания можно взять здесь: Will It Shuffle?

Смещение видно невооруженным глазом — диагональная зеленая линия показывает, что изначальный массив почти не перемешан. Это не значит, что в Chrome сортировка „лучше“, чем в Firefox. Это говорит лишь о том, что не следует использовать компаратор на случайных числах. Такие компараторы не способны правильно функционировать.

Перевод статьи «Visualizing Algorithms»