Алгоритмы и структуры данных для начинающих: стеки и очереди

В предыдущих частях мы рассматривали базовые структуры данных, которые, по сути, являлись надстройками над массивом. В этой статье мы добавим к коллекциям простые операции и посмотрим, как это повлияет на их возможности.

Также смотрите другие материалы этой серии: бинарное дерево, динамический массив, связный список, оценка сложности алгоритма, сортировка и множества.

Стек

Стек — это коллекция, элементы которой получают по принципу «последний вошел, первый вышел» (Last-In-First-Out или LIFO). Это значит, что мы будем иметь доступ только к последнему добавленному элементу.

В отличие от списков, мы не можем получить доступ к произвольному элементу стека. Мы можем только добавлять или удалять элементы с помощью специальных методов. У стека нет также метода Contains, как у списков. Кроме того, у стека нет итератора. Для того, чтобы понимать, почему на стек накладываются такие ограничения, давайте посмотрим на то, как он работает и как используется.

Наиболее часто встречающаяся аналогия для объяснения стека — стопка тарелок. Вне зависимости от того, сколько тарелок в стопке, мы всегда можем снять верхнюю. Чистые тарелки точно так же кладутся на верх стопки, и мы всегда будем первой брать ту тарелку, которая была положена последней.

Если мы положим, например, красную тарелку, затем синюю, а затем зеленую, то сначала надо будет снять зеленую, потом синюю, и, наконец, красную. Главное, что надо запомнить — тарелки всегда ставятся и на верх стопки. Когда кто-то берет тарелку, он также снимает ее сверху. Получается, что тарелки разбираются в порядке, обратном тому, в котором ставились.

Теперь, когда мы понимаем, как работает стек, введем несколько терминов. Операция добавления элемента на стек называется «push», удаления — «pop». Последний добавленный элемент называется верхушкой стека, или «top», и его можно посмотреть с помощью операции «peek». Давайте теперь посмотрим на заготовку класса, реализующего стек.

Класс Stack

Класс Stack определяет методы Push, Pop, Peek для доступа к элементам и поле Count. В реализации мы будем использовать LinkedList<T> для хранения элементов.

			public class Stack
{
    LinkedList _items = new LinkedList();

    public void Push(T value)
    {
        throw new NotImplementedException();
    }

    public T Pop()
    {
        throw new NotImplementedException();
    }

    public T Peek()
    {
        throw new NotImplementedException();
    }

    public int Count
    {
        get;
    }
}
		

Метод Push

• Поведение: Добавляет элемент на вершину стека.
• Сложность: O(1).

Поскольку мы используем связный список для хранения элементов, можно просто добавить новый в конец списка.

			public void Push(T value)
{
    _items.AddLast(value);
}
		

Метод Pop

• Поведение: Удаляет элемент с вершины стека и возвращает его. Если стек пустой, кидает InvalidOperationException.
• Сложность: O(1).

Push добавляет элементы в конец списка, поэтому забирать их будет также с конца. В случае, если список пуст, будет выбрасываться исключение.

			public T Pop()
{
    if (_items.Count == 0)
    {
        throw new InvalidOperationException("The stack is empty");
    }

    T result = _items.Tail.Value;

    _items.RemoveLast();

    return result;
}
		

Метод Peek

• Поведение: Возвращает верхний элемент стека, но не удаляет его. Если стек пустой, кидает InvalidOperationException.
• Сложность: O(1).

			public T Peek()
{
    if (_items.Count == 0)
    {
        throw new InvalidOperationException("The stack is empty");
    }

    return _items.Tail.Value;
}
		

Метод Count

• Поведение: Возвращает количество элементов в стеке.
• Сложность: O(1).

Зачем нам знать, сколько элементов находится в стеке, если мы все равно не имеем к ним доступа? С помощью этого поля мы можем проверить, есть ли элементы на стеке или он пуст. Это очень полезно, учитывая, что метод Pop кидает исключение.

			public int Count
{
    get
    {
        return _items.Count;
    }
}
		

Пример: калькулятор в обратной польской записи

Классический пример использования стека — калькулятор в обратной польской, или постфиксной, записи. В ней оператор записывается после своих операндов. То есть, мы пишем:

			<операнд> <операнд> <оператор>
		

вместо традиционного:

			<операнд> <оператор> <операнд>
		

Другими словами, вместо «4 + 2» мы запишем «4 2 +». Если вам интересно происхождение обратной польской записи и ее названия, вы можете узнать об этом на Википедии или в поисковике.

То, как вычисляется обратная польская запись и почему стек так полезен при ее использовании, хорошо видно из следующего алгоритма:

			for each input value
    if the value is an integer
        push the value on to the operand stack
    else if the value is an operator
        pop the left and right values from the stack
        evaluate the operator
        push the result on to the stack
pop answer from stack.
		

То есть, для выражения «4 2 +» действия будут следующие:

			push(4)
push(2)
push(pop() + pop())
		

В конце на стеке окажется одно значение — 6.

Далее приводится полный код простого калькулятора, который считывает выражение (например, 4 2 +) из консоли, разбивает входные данные по пробелам (["4", "2", "+"]) и выполняет алгоритм вычисления. Вычисление продолжается до тех пор, пока не будет встречено слово quit.

			void RpnLoop()
{
    while (true)
    {
        Console.Write("> ");
        string input = Console.ReadLine();
        if (input.Trim().ToLower() == "quit")
        {
            break;
        }
        // Стек еще не обработанных значений.
        Stack values = new Stack();

        foreach (string token in input.Split(new char[] { ' ' }))
        {
            // Если значение - целое число...
            int value;
            if (int.TryParse(token, out value))
            {
                // ... положить его на стек.
                values.Push(value);
            }
            else
            {
                // в противном случае выполнить операцию...
                int rhs = values.Pop();
                int lhs = values.Pop();

                // ... и положить результат обратно.
                switch (token)
                {
                    case "+":
                        values.Push(lhs + rhs);
                        break;
                    case "-":
                        values.Push(lhs - rhs);
                        break;
                    case "*":
                        values.Push(lhs * rhs);
                        break;
                    case "/":
                        values.Push(lhs / rhs);
                        break;
                    case "%":
                        values.Push(lhs % rhs);
                        break;
                    default:
                        // Если операция не +, -, * или /
                        throw new ArgumentException(
                            string.Format("Unrecognized token: {0}", token));
                }
            }
        }

        // Последний элемент на стеке и есть результат.
        Console.WriteLine(values.Pop());
    }
}
		

Очередь

Очереди очень похожи на стеки. Они также не дают доступа к произвольному элементу, но, в отличие от стека, элементы кладутся (enqueue) и забираются (dequeue) с разных концов. Такой метод называется «первый вошел, первый вышел» (First-In-First-Out или FIFO). То есть забирать элементы из очереди мы будем в том же порядке, что и клали. Как реальная очередь или конвейер.

Очереди часто используются в программах для реализации буфера, в который можно положить элемент для последующей обработки, сохраняя порядок поступления. Например, если база данных поддерживает только одно соединение, можно использовать очередь потоков, которые будут, как ни странно, ждать своей очереди на доступ к БД.

Класс Queue

Класс Queue, как и стек, будет реализован с помощью связного списка. Он будет предоставлять методы Enqueue для добавления элемента, Dequeue для удаления, Peek и Count. Как и класс Stack, он не будет реализовывать интерфейс ICollection<T>, поскольку это коллекции специального назначения.

			public class Queue
{
    LinkedList _items = new LinkedList();

    public void Enqueue(T value)
    {
        throw new NotImplementedException();
    }

    public T Dequeue()
    {
        throw new NotImplementedException();
    }

    public T Peek()
    {
        throw new NotImplementedException();
    }

    public int Count
    {
        get;
    }
}
		

Метод Enqueue

• Поведение: Добавляет элемент в очередь.
• Сложность: O(1).

Новые элементы очереди можно добавлять как в начало списка, так и в конец. Важно только, чтобы элементы доставались с противоположного края. В данной реализации мы будем добавлять новые элементы в начало внутреннего списка.

			Public void Enqueue(T value)
{
    _items.AddFirst(value);
}
		

Метод Dequeue

• Поведение: Удаляет первый помещенный элемент из очереди и возвращает его. Если очередь пустая, кидает InvalidOperationException.
• Сложность: O(1).

Поскольку мы вставляем элементы в начало списка, убирать мы их будем с конца. Если список пуст, кидается исключение.

			public T Dequeue()
{
    if (_items.Count == 0)
    {
        throw new InvalidOperationException("The queue is empty");
    }

    T last = _items.Tail.Value;

    _items.RemoveLast();

    return last;
}
		

Метод Peek

• Поведение: Возвращает элемент, который вернет следующий вызов метода Dequeue. Очередь остается без изменений. Если очередь пустая, кидает InvalidOperationException.
• Сложность: O(1).

			public T Peek()
{
    if (_items.Count == 0)
    {
        throw new InvalidOperationException("The queue is empty");
    }

    return _items.Tail.Value;
}
		

Метод Count

• Поведение: Возвращает количество элементов в очереди или 0, если очередь пустая.
• Сложность: O(1).

			public int Count
{
    get
    {
        return _items.Count;
    }
}
		

Двусторонняя очередь

Двусторонняя очередь (Double-ended queue), или дек (Deque), расширяет поведение очереди. В дек можно добавлять или удалять элементы как с начала, так и с конца очереди. Такое поведение полезно во многих задачах, например, планирование выполнения потоков или реализация других структур данных. Позже мы рассмотрим вариант реализации стека с помощью двусторонней очереди.

Класс Deque

Класс Deque проще всего реализовать с помощью двусвязного списка. Он позволяет просматривать, удалять и добавлять элементы в начало и в конец списка. Основное отличие двусторонней очереди от обычной — методы Enqueue, Dequeue, и Peek разделены на пары для работы с обоими концами списка.

			public class Deque
{
    LinkedList _items = new LinkedList();

    public void EnqueueFirst(T value)
    {
        throw new NotImplementedException();
    }

    public void EnqueueLast(T value)
    {
        throw new NotImplementedException();
    }

    public T DequeueFirst()
    {
        throw new NotImplementedException();
    }

    public T DequeueLast()
    {
        throw new NotImplementedException();
    }

    public T PeekFirst()
    {
        throw new NotImplementedException();
    }

    public T PeekLast()
    {
        throw new NotImplementedException();
    }

    public int Count
    {
        get;
    }
}
		

Метод EnqueueFirst

• Поведение: Добавляет элемент в начало очереди. Этот элемент будет взят из очереди следующим при вызове метода DequeueFirst.
• Сложность: O(1).

			public void EnqueueFirst(T value)
{
    _items.AddFirst(value);
}
		

Метод EnqueueLast

• Поведение: Добавляет элемент в конец очереди. Этот элемент будет взят из очереди следующим при вызове метода DequeueLast.
• Сложность: O(1).

			public void EnqueueLast(T value)
{
    _items.AddLast(value);
}
		

Метод DequeueFirst

• Поведение: Удаляет элемент из начала очереди и возвращает его. Если очередь пустая, кидает InvalidOperationException.
• Сложность: O(1).

			public T DequeueFirst()
{
    if (_items.Count == 0)
    {
        throw new InvalidOperationException("DequeueFirst called when deque is empty");
    }

    T temp = _items.Head.Value;

    _items.RemoveFirst();

    return temp;
}
		

Метод DequeueLast

• Поведение: Удаляет элемент с конца очереди и возвращает его. Если очередь пустая, кидает InvalidOperationException.
• Сложность: O(1).

			public T DequeueLast()
{
    if (_items.Count == 0)
    {
        throw new InvalidOperationException("DequeueLast called when deque is empty");
    }

    T temp = _items.Tail.Value;

    _items.RemoveLast();

    return temp;
}
		

Метод PeekFirst

• Поведение: Возвращает элемент из начала очереди, не изменяя ее. Если очередь пустая, кидает InvalidOperationException.
• Сложность: O(1).

			public T PeekFirst()
{
    if (_items.Count == 0)
    {
        throw new InvalidOperationException("PeekFirst called when deque is empty");
    }

    return _items.Head.Value;
}
		

Метод PeekLast

• Поведение: Возвращает элемент с конца очереди, не изменяя ее. Если очередь пустая, кидает InvalidOperationException.
• Сложность: O(1).

			public T PeekLast()
{
    if (_items.Count == 0)
    {
        throw new InvalidOperationException("PeekLast called when deque is empty");
    }

    return _items.Tail.Value;
}
		

Метод Count

• Поведение: Возвращает количество элементов в очереди или 0, если очередь пустая.
• Сложность: O(1).

			public int Count
{
    get
    {
        return _items.Count;
    }
}
		

Пример: реализация стека

Двусторонняя очередь часто используется для реализации других структур данных. Давайте посмотрим на пример реализации стека с ее помощью.

У вас, возможно, возник вопрос, зачем реализовывать стек на основе очереди вместо связного списка. Причины две: производительность и повторное использование кода. У связного списка есть накладные расходы на создание узлов и нет гарантии локальности данных: элементы могут быть расположены в любом месте памяти, что вызывает большое количество промахов и падение производительности на уровне процессоров. Более производительная реализация двусторонней очереди требует массива для хранения элементов.

Тем не менее, реализация стека или очереди с помощью массива — непростая задача, но такая реализация двусторонней очереди и использование ее в качестве основы для других структур данных даст нам серьезный плюс к производительности и позволит повторно использовать код. Это снижает стоимость поддержки.

Позже мы посмотрим на вариант очереди с использованием массива, но сначала давайте взглянем на класс стека с использованием двусторонней очереди:

			public class Stack
{
    Deque _items = new Deque();

    public void Push(T value)
    {
        _items.EnqueueFirst(value);
    }

    public T Pop()
    {
        return _items.DequeueFirst();
    }

    public T Peek()
    {
        return _items.PeekFirst();
    }

    public int Count
    {
        get
        {
            return _items.Count;
        }
    }
}
		

Заметьте, что вся обработка ошибок теперь лежит на классе Deque, и, кроме того, любая оптимизация очереди также отразится на стеке. Реализация обычной очереди на основе двусторонней настолько проста, что мы оставим ее читателю в качестве упражнения.

Хранение элементов в массиве

Как уже было упомянуто, у реализации очереди с использованием массива есть свои преимущества. Она выглядит простой, но на самом деле есть ряд нюансов, которые надо учесть.

Давайте посмотрим на проблемы, которые могут возникнуть, и на их решение. Кроме того, нам понадобится информация об увеличении внутреннего массива из прошлой статьи о динамических массивах.

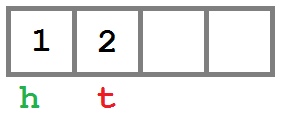
При создании очереди у нее внутри создается массив нулевой длины. Красные буквы «h» и «t» означают указатели _head и _tail соответственно.

			Deque deq = new Deque();
deq.EnqueueFirst(1);
		

Добавляем элемент в начало

			deq.EnqueueLast(2);
		

Добавляем элемент в конец

			deq.EnqueueFirst(0);
		

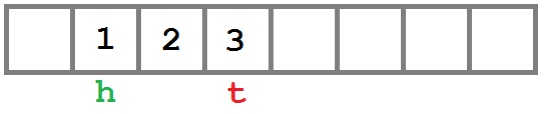
Добавляем еще один элемент в начало

Обратите внимание: индекс «головы» очереди перескочил в начало списка. Теперь первый элемент, который будет возвращен при вызове метода DequeueFirst — 0 (индекс 3).

			deq.EnqueueLast(3);
		

И еще один в конец

Массив заполнен, поэтому при добавлении элемента произойдет следующее:

• Алгорим роста определит размер нового массива.
• Элементы скопируются в новый массив с «головы» до «хвоста».
• Добавится новый элемент.

			deq.EnqueueLast(4);
		

Добавляем значение в конец расширенного массива

Теперь посмотрим, что происходит при удалении элемента:

			deq.DequeueFirst();
		

Удаляем элемент из начала

			deq.DequeueLast();
		

Удаляем элемент с конца

Ключевой момент: вне зависимости от вместимости или заполненности внутреннего массива, логически, содержимое очереди — элементы от «головы» до «хвоста» с учетом «закольцованности». Такое поведение также называется «кольцевым буфером».

Теперь давайте посмотрим на реализацию.

Класс Deque (с использованием массива)

Интерфейс очереди на основе массива такой же, как и в случае реализации через связный список. Мы не будем его повторять. Однако, поскольку список был заменен на массив, у нас добавились новые поля — сам массив, его размер и указатели на «хвост» и «голову» очереди.

			public class Deque
{
    T[] _items = new T[0];

    // Количество элементов в очереди.
    int _size = 0;

    // Индекс первого (самого старого) элемента.
    int _head = 0;

    // Индекс последнего (самого нового) элемента.
    int _tail = -1;
...
}
		

Алгоритм роста

Когда свободное место во внутреннем массиве заканчивается, его необходимо увеличить, скопировать элементы и обновить указатели на «хвост» и «голову». Эта операция производится при необходимости во время добавления элемента. Параметр startingIndex используется, чтобы показать, сколько полей в начале необходимо оставить пустыми (в случае добавления в начало).

Обратите внимание на то, как извлекаются данные, когда приходится переходить в начало массива при проходе от «головы» к «хвосту».

			private void allocateNewArray(int startingIndex)
{
    int newLength = (_size == 0) ? 4 : _size * 2;

    T[] newArray = new T[newLength];

    if (_size > 0)
    {
        int targetIndex = startingIndex;

// Копируем содержимое...
// Если массив не закольцован, просто копируем элементы.
// В противном случае, копирует от head до конца,
// а затем от начала массива до tail.

        // Если tail меньше, чем head, переходим в начало.
        if (_tail < _head)
        {
// Копируем _items[head].._items[end] в newArray[0]..newArray[N].
            for (int index = _head; index < _items.Length; index++)
            {
                newArray[targetIndex] = _items[index];
                targetIndex++;
            }

// Копируем _items[0].._items[tail] в newArray[N+1]..
            for (int index = 0; index <= _tail; index++)
            {
                newArray[targetIndex] = _items[index];
                targetIndex++;
            }
        }
        else
        {
// Копируем _items[head].._items[tail] в newArray[0]..newArray[N]
            for (int index = _head; index <= _tail; index++)
            {
                newArray[targetIndex] = _items[index];
                targetIndex++;
            }
        }


        _head = startingIndex;
        _tail = targetIndex - 1;
    }
    else
    {
        // Массив пуст.
        _head = 0;
        _tail = -1;
    }

    _items = newArray;
}
		

Метод EnqueueFirst

• Поведение: Добавляет элемент в начало очереди. Этот элемент будет взят из очереди следующим при вызове метода DequeueFirst.
• Сложность: O(1) в большинстве случаев; O(n), когда нужно расширение массива.

			public void EnqueueFirst(T item)
{
    // Проверим, необходимо ли увеличение массива:
    if (_items.Length == _size)
    {
        allocateNewArray(1);
    }

    // Так как массив не заполнен и _head больше 0,
    // мы знаем, что есть место в начале массива.
    if (_head > 0)
    {
        _head--;
    }
    else
    {
        // В противном случае мы должны закольцеваться.
        _head = _items.Length - 1;
    }

    _items[_head] = item;


    _size++;

    if (_size == 1)
    {
        // Если мы добавили первый элемент в пустую
        // очередь, он же будет и последним, поэтому
        // нужно обновить и _tail.
        _tail = _head;
    }
}
		

Метод EnqueueLast

• Поведение: Добавляет элемент в конец очереди. Этот элемент будет взят из очереди следующим при вызове метода DequeueLast.
• Сложность: O(1) в большинстве случаев; O(n), когда нужно расширение массива.

			public void EnqueueLast(T item)
{
    // Проверим, необходимо ли увеличение массива:
    if (_items.Length == _size)
    {
        allocateNewArray(0);
    }

    // Теперь, когда у нас есть подходящий массив,
    // если _tail в конце массива, нам надо перейти в начало.
    if (_tail == _items.Length - 1)
    {
        _tail = 0;
    }
    else
    {
        _tail++;
    }

    _items[_tail] = item;
    _size++;

    if (_size == 1)
    {
        // Если мы добавили последний элемент в пустую
        // очередь, он же будет и первым, поэтому
        // нужно обновить и _head.
        _head = _tail;
    }
}
		

Метод DequeueFirst

• Поведение: Удаляет элемент с начала очереди и возвращает его. Если очередь пустая, кидает InvalidOperationException.
• Сложность: O(1).

			public T DequeueFirst()
{
    if (_size == 0)
    {
        throw new InvalidOperationException("The deque is empty");
    }

    T value = _items[_head];

    if (_head == _items.Length - 1)
    {
// Если head установлен на последнем индексе,
// переходим к началу массива.
        _head = 0;
    }
    else
    {
// Переходим к следующему элементу.
        _head++;
    }

    _size--;

    return value;
}
		

Метод DequeueLast

• Поведение: Удаляет элемент с конца очереди и возвращает его. Если очередь пустая, кидает InvalidOperationException.
• Сложность: O(1).

			public T DequeueLast()
{
    if (_size == 0)
    {
        throw new InvalidOperationException("The deque is empty");
    }

    T value = _items[_tail];

    if (_tail == 0)
    {
// Если tail установлен на начало массива, переходим к концу.
        _tail = _items.Length - 1;
    }
    else
    {
// Переходим к предыдущему элементу.
        _tail--;
    }

    _size--;

    return value;
}
		

Метод PeekFirst

• Поведение: Возвращает элемент с начала очереди, не изменяя ее. Если очередь пустая, кидает InvalidOperationException.
• Сложность: O(1).

			public T PeekFirst()
{
    if (_size == 0)
    {
        throw new InvalidOperationException("The deque is empty");
    }

    return _items[_head];
}
		

Метод PeekLast

• Поведение: Возвращает элемент с конца очереди, не изменяя ее. Если очередь пустая, кидает InvalidOperationException.
• Сложность: O(1).

			public T PeekLast()
{
    if (_size == 0)
    {
        throw new InvalidOperationException("The deque is empty");
    }

    return _items[_tail];
}
		

Метод Count

• Поведение: Возвращает количество элементов в очереди или 0, если очередь пустая.
• Сложность: O(1).

			public int Count
{
    get
    {
        return _size;
    }
}
		

Продолжение следует

Вот мы и закончили четвертую часть нашего цикла статей. В ней мы рассмотрели стеки и очереди. В следующий раз мы перейдем к бинарным деревьям поиска.
Перевод статьи «Stacks and Queues»