Задача на собеседовании: провести прямую через набор точек
Ищем наиболее вероятные положения автономного автомобиля, который едет прямо по дороге и отслеживается по GPS.
39К открытий43К показов
Дмитрий Хизбуллин
ведущий инженер в исследовательском центре Huawei
Будучи энтузиастом в области беспилотных автомобилей, я проходил собеседования в ряд компаний на позицию разработчика программного обеспечения. Чаще всего компании, занимающиеся беспилотными автомобилями, разрабатывают машину, которая может проехать по местности и хорошо ориентируется в 3D окружении. Следовательно, фирмы беспокоятся о том, насколько хорош кандидат в вычислительной геометрии, и в частности, как легко и быстро он/она может закодить решение. Один из вопросов на собеседовании меня особенно заинтересовал. Задача формулируется следующим образом:
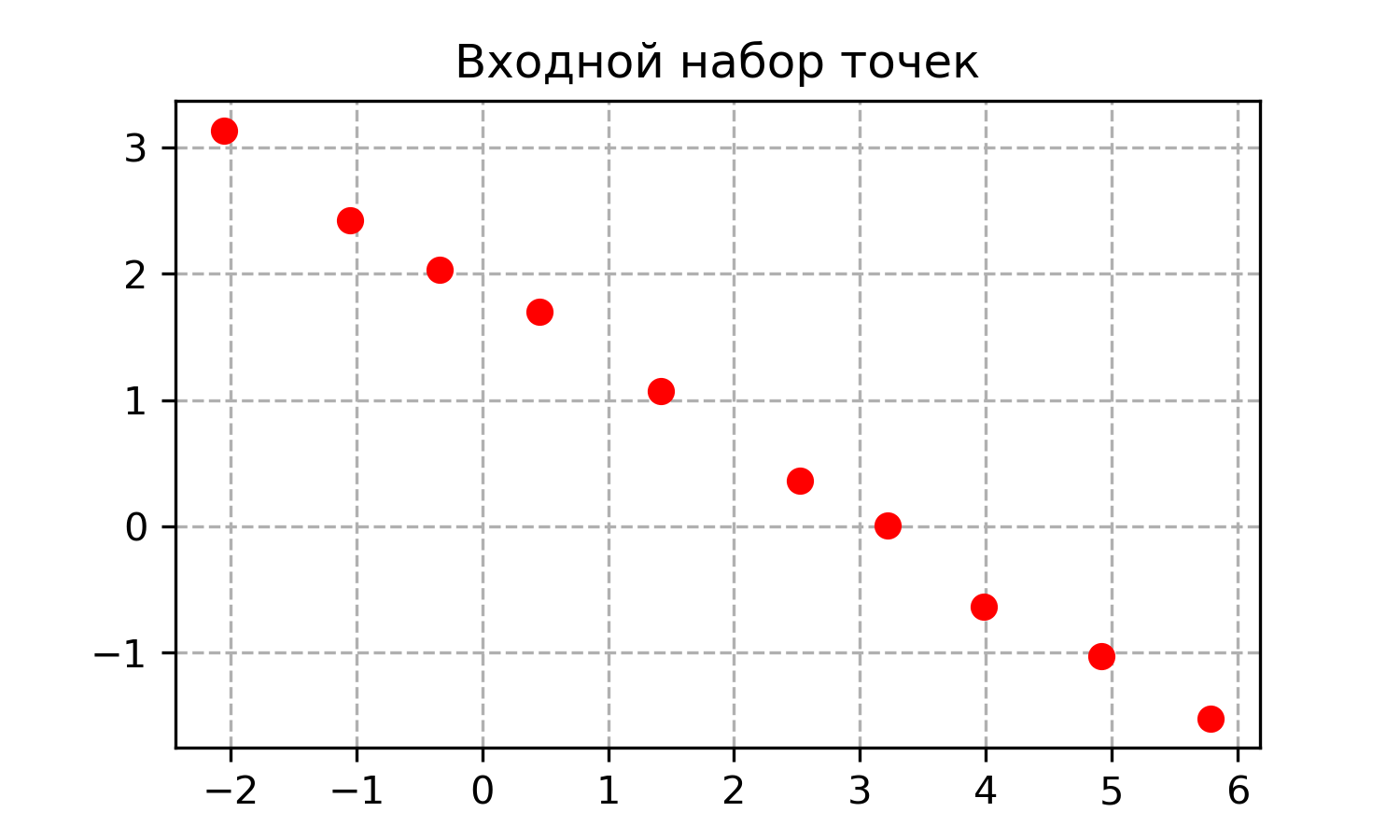
Представьте, что ваш автономный автомобиль едет по дороге прямо, и его 2D позиции определяются при помощи ГНСС (Глобальной Навигационной Спутниковой Системы, например GPS) не очень точно, а с определенной погрешностью. Требуется найти наиболее вероятные положения автомобиля такие, что они лежат на одной прямой.
Эту задачу, как и практически любую другую, можно решать несколькими способами. В этой статье мы рассмотрим 3 решения на языке Python и сравним их: посмотрим на достоинства и недостатки. С математической точки зрения задание формулируется как задача линейной регрессии: найти аппроксимацию набора точек при помощи прямой. С программисткой стороны нам понадобится подходящая библиотека по манипулированию векторами и матрицами. Мы будем использовать NumPy для этой цели.
Подход 1: Метод наименьших квадратов
На первый взгляд, нам подойдет стандартное решение линейной регрессии: метод наименьших квадратов.
Нам дан массив 2D координат, представляющих собой пары точек (x, y). Мы можем считать x за аргумент, а y — за значение функции. Тогда, проконсультировавшись с Википедией, мы можем рассчитать коэффициенты прямой при помощи следующей формулы.
Это хорошее решение в том плане, что оно прямолинейное (непреднамеренный каламбур), то есть нам нужно взять и рассчитать все по формуле и получить ответ. Недолго думая, закодим решение. Далее я предлагаю читателю следовать за комментариями в коде.
Посмотрим, что мы получили на выходе.
Выглядит в точности так, как мы и хотели, — линия прямая и максимально подогнана под набор точек. Однако у метода наименьших квадратов есть один существенный недостаток — он не работает в случае, если траектория вертикальная. В таком случае наклон прямой обращается в бесконечность, и программа или упадет, или выдаст NaN — «не число». Таким образом, данный подход не может претендовать на продуктовый уровень.
Подход 2: RANSAC
RANSAC — метод достижения консенсуса на основе случайных выборок, предложенный в 1981 году.
В нашем двумерном случае мы будем случайно выбирать две точки (суппорт) из входного массива и проверять, насколько хорошо все входные точки вписывается в полосу ближайшей окрестности прямой, задаваемой суппортом. Конечно же не каждая попытка даст удачно угаданную прямую, поэтому алгоритм RANSAC — итерационный. Для RANSAC есть формула, позволяющая по ожидаемому проценту выбросов и желаемой вероятности успешного решения вычислить необходимое количество итераций алгоритма.
где p — вероятность успеха, ω — доля выбросов, n — размер суппорта. В нашем случае размер суппорта равен двум точкам для прямой в двумерном пространстве. Для прямой в трехмерном пространстве n было бы тоже равно двум, а для трехмерной плоскости в 3D — уже трем точкам. В примере кода количество итераций получилось 16, что является вполне небольшим значением. Я предлагаю читателю далее следовать за комментариями в коде.
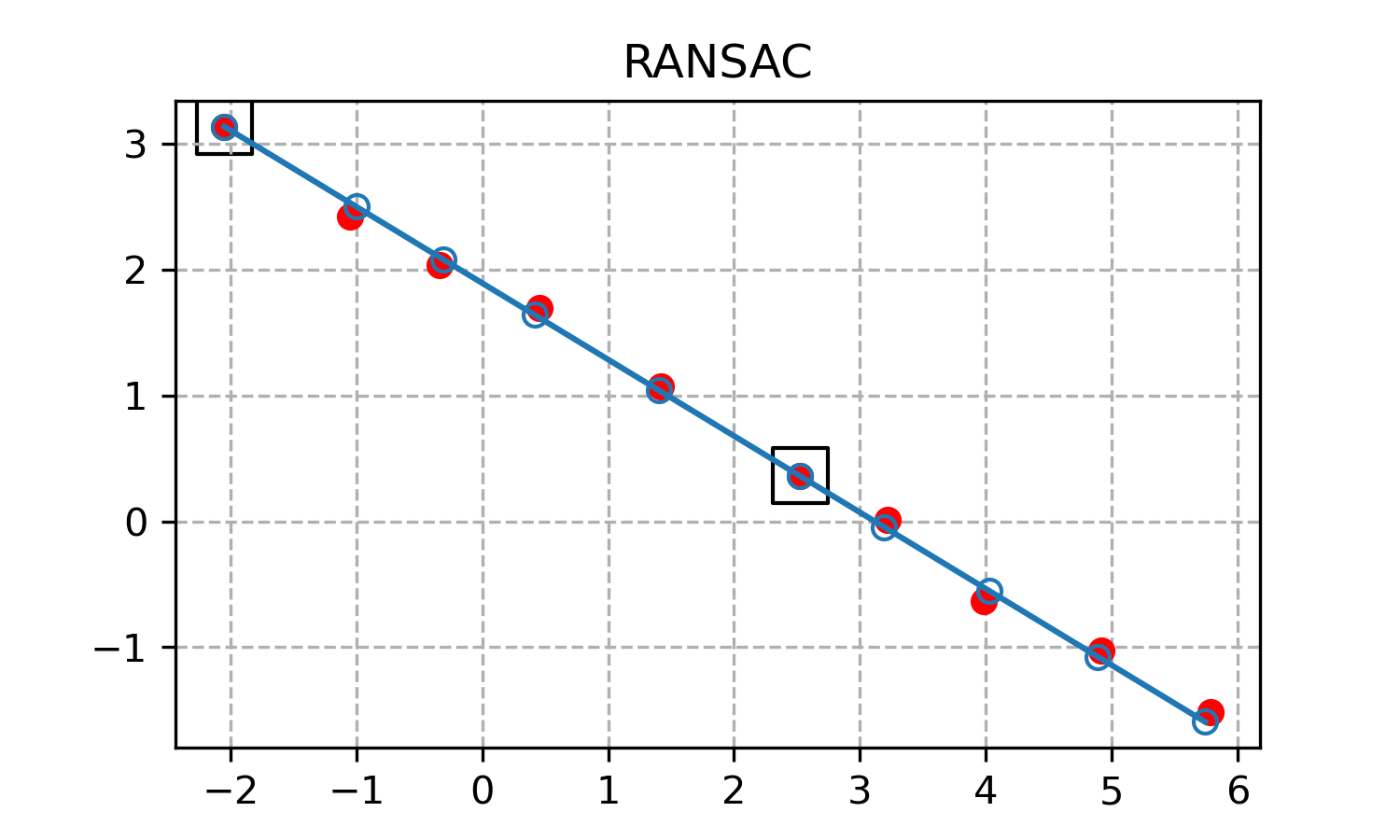
Что мы получим, запустив код?
Полученная прямая хорошо аппроксимирует набор точек. Черными квадратами отмечены точки, которые были выбраны в качестве суппорта.
В чем недостатки метода RANSAC? В том, что он не гарантирует успешного результата. Вероятность того, что генератор случайных чисел будет выбирать исключительно выбросы или просто неудачные точки, например очень близкие друг к другу, достаточно мала. Тем не менее, в применениях, требующий высокой надежности, например, в беспилотных автомобилях, RANSAC может не подойти. Также RANSAC не подойдет там, где доступ к генератору случайных или псевдослучайных чисел затруднен. Помимо того у RANSAC есть много параметров, которые надо подбирать под задачу. В частности, max_distance довольно сложно оценить, не потратив длительное время на изучение интенсивности шума.
Подход 3: PCA
Метод главных компонент (Principal Component Analysis, PCA) часто используется для уменьшения размерности данных, когда нужно аффинно преобразовать облако точек таким образом, чтобы по большинству размерностей дисперсия была малой (или хотя бы меньшей, чем по важным размерностям). В таком случае можно отбросить эти размерности, как не несущие информации. Очень похоже на нашу ситуацию, когда нам нужно отбросить шум в направлении, перпендикулярном общему направлению разброса точек, и таким образом спроецировать точки на соответствующую прямую.
В результате вычисления собственных чисел и собственных векторов мы получим пары (собственное число, собственный вектор). Чем больше собственное число, тем выше разброс точек в направлении соответствующего собственного вектора. Применительно к нашему случаю нам как раз нужно найти собственный вектор с наибольшим собственным значением. Он и задаст прямую, на которую мы будем проецировать точки. Код с комментариями:
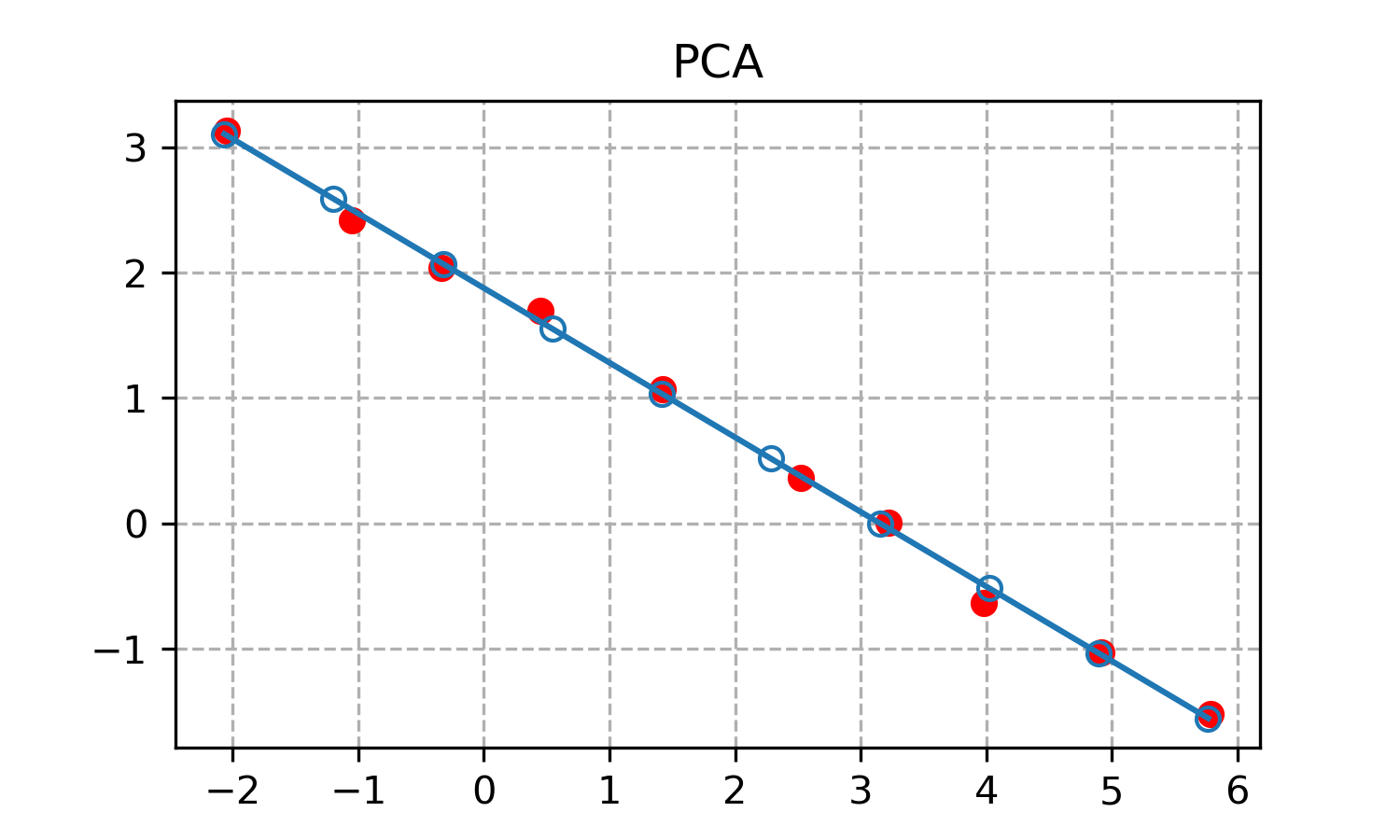
Запустив код, получаем следующий график.
PCA также справился с задачей! При этом этот метод лишен недостатка метода наименьших квадратов: PCA отлично аппроксимирует вертикальные линии. Также PCA всегда даст результат в отличие от вероятностного RANSAC. Однако, в отличие от RANSAC метод PCA чувствителен к сильным выбросам в локациях точек.
Заключение
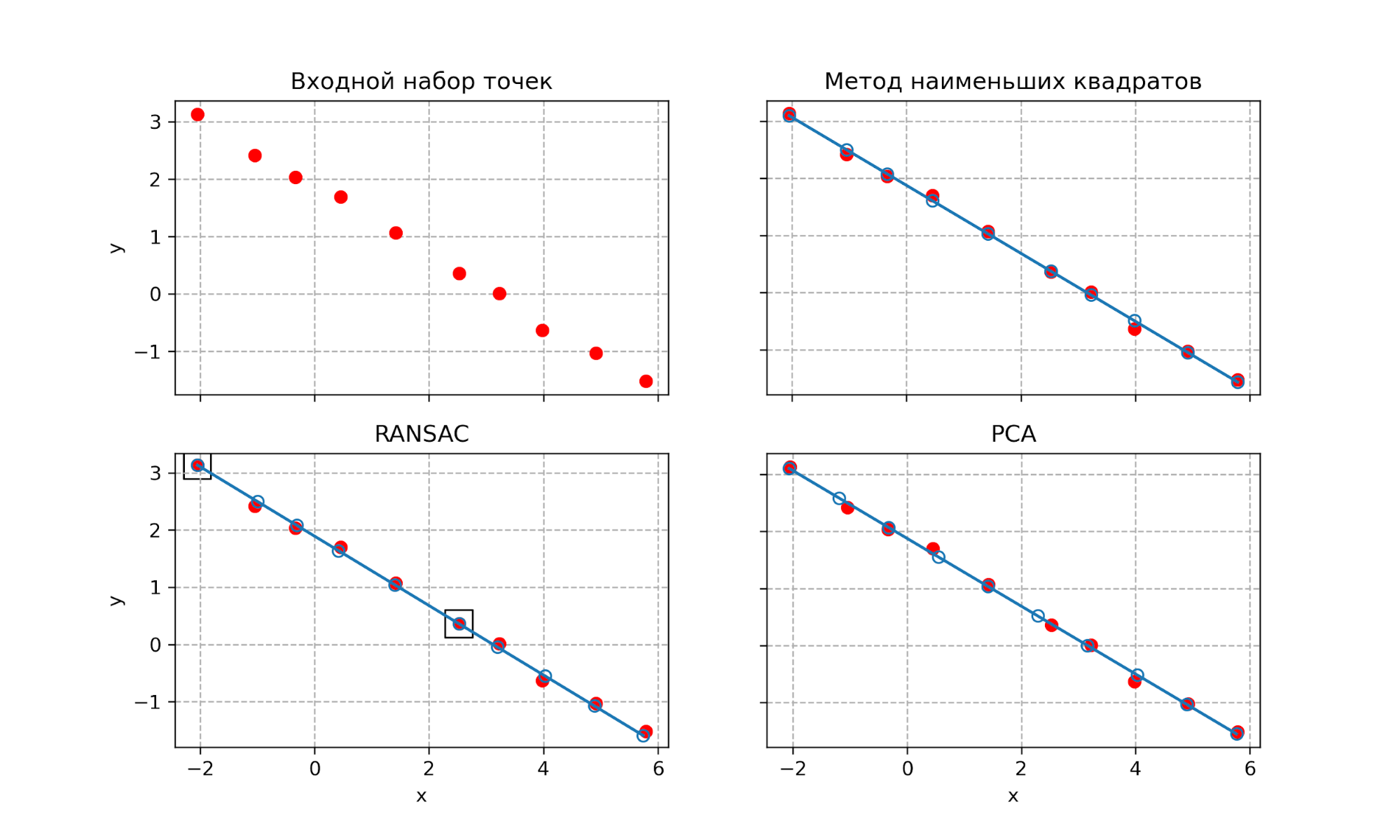
Данная задача понравилась мне тем, что у нее есть несколько существенно разных решений со своими присущими достоинствами и недостатками. Также задача позволяет разобраться с матричными операциями в NumPy на простом примере. Посмотрим на все три решения на одном изображении.
Из трех решений мой личный фаворит — метод главных компонент PCA.
Дорогой читатель, надеюсь статья тебе понравилась и ты приобрел навыки превращения задач аналитической геометрии в код. Полный код доступен на GitHub.
Спасибо за внимание и удачи на собеседованиях!
39К открытий43К показов