JavaScript для продвинутых: пишем симулятор гравитации

Космос трудно понять — или люди склонны так думать. Но в этом уроке мы увидим, что законы, управляющие движением звёзд, планет, астероидов и даже целых галактик, невероятно просты. Если бы наша Вселенная была создана разработчиком, он наверняка был бы обеспокоен написанием чистого кода, который легко поддерживать и масштабировать.

Мы собираемся создать симуляцию внутренней области нашей Солнечной системы, используя только старый добрый JavaScript. Это будет гравитационная N-объектная симуляция, где каждый объект испытывает на себе гравитацию всех других объектов симуляции.

Мы также посмотрим, как позволить пользователям добавлять свои собственные планеты при помощи небольшого движения мыши, и вызывать при этом всевозможный космический беспорядок. Ещё мы разберёмся, как создать несколько необычных траекторий движения тел, в дополнение к некоторым другим фишкам, которые сделают симулятор более увлекательным для обычного пользователя.

Примечание Это руководство предполагает, что у вас есть базовые знания JavaScript, а также синтаксиса и нововведений, представленных в ES6.

Написание алгоритма для N-объектной симуляции

Для написания алгоритма мы будем опираться на численное интегрирование. Оно хорошо подходит для решения гравитационных N-объектных задач, в которых оперируют позициями и скоростями всех объектов в данный момент времени T, вычисляют гравитационную силу, с которой они действуют друг на друга, и изменяют их скорости и позиции во времени (T + dt, dt — изменение во времени). Применяя это, мы можем проследить траектории множества тел в пространстве и времени.

Для моделирования будем использовать декартову систему координат. Преимущество использования такой системы координат для моделирования в том, что Canvas API, с помощью которого мы будем визуализировать моделирование, также её использует.

Для написания алгоритма необходимо иметь представление о том, что подразумевается под скоростью и ускорением. Скорость — это изменение положения объекта во времени, а ускорение — изменение скорости объекта во времени. Первый закон Ньютона гласит, что каждый объект будет оставаться в покое или двигаться равномерно и прямолинейно, если на него не будут воздействовать никакие внешние силы. Земля не движется по прямой линии, а вращается вокруг Солнца, поэтому она ускоряется. Это ускорение вызывают гравитационные силы Солнца и других планет и объектов во Вселенной, действующие на Землю.

Для начала напишем некоторый псевдокод для обновления позиций и скоростей тел в декартовом пространстве. Будем хранить тела как объекты в массиве, где каждый объект представляет собой небесное тело с координатами положения x, y и z и векторами скорости. Векторы скорости имеют префикс v.

			const updatePositionVectors = (masses, dt) => {
  const massesLen = masses.length;

  for (let i = 0; i < massesLen; i++) {
    const massI = masses[i];

    mass.x += mass.vx * dt;
    mass.y += mass.vy * dt;
    mass.z += mass.vz * dt;
  }
};

const updateVelocityVectors = (masses, dt) => {
  const massesLen = masses.length;

  for (let i = 0; i < massesLen; i++) {
    const massI = masses[i];

    massI.vx += massI.ax * dt;
    massI.vy += massI.ay * dt;
    massI.vz += massI.az * dt;
  }
};
		

Из фрагмента видно, что на каждом временном шаге (dt) мы обновляем значения скорости моделируемых тел и их позиции. Также видна взаимосвязь между положением и скоростью тела. Изменение положения тела равно произведению вектора скорости на dt. Точно так же можно разобрать связь между скоростью и ускорением.

Чтобы получить векторы ускорения тела (чтобы можно было рассчитать изменение его векторов скорости) необходимо получить результат взаимодействия massJ с вектором ускорения massI. Для этого нужно рассчитать гравитационную силу, которую оказывает massJ на massI, а затем, чтобы получить вектор ускорения, например, х, просто вычислить произведение этой силы на расстояние между двумя массами на оси x. Чтобы получить векторы ускорения y и z, нужно проделать то же самое. Теперь необходимо выяснить, как рассчитать гравитационную силу, которую оказывает massJ на massI. Формула выглядит следующим образом:

			f = g * massJ.m / dSq * (dSq + s)^½
		

Приведённая выше формула показывает: гравитационное воздействие massJ на massI равно произведению гравитационной постоянной g на massJ (massJ.m), делённому на произведение суммы квадратов расстояния между massI и massJ по осям x, y и z (dSq) и квадратному корню из (dSq + s), где s — это так называемая константа размягчения (softeningConstant). Включение в гравитационные расчёты константы смягчения предотвращает ситуацию, когда сила гравитации, создаваемая massJ, становится бесконечно большой, поскольку она слишком близка к massI. Эта «ошибка» в ньютоновской теории гравитации возникает по той причине, что ньютоновская гравитация рассматривает массы как точечные объекты, которыми они на самом деле не являются. Чтобы получить суммарное ускорение massI вдоль, например, оси x, мы просто суммируем ускорение, возникающее из-за воздействия других тел в симуляции.

Преобразуем вышесказанное в код для обновления векторов ускорения всех тел.

			const updateAccelerationVectors = (masses, g, softeningConstant) => {
  const massesLen = masses.length;

  for (let i = 0; i < massesLen; i++) {
    let ax = 0;
    let ay = 0;
    let az = 0;

    const massI = masses[i];

    for (let j = 0; j < massesLen; j++) {
      if (i !== j) {
        const massJ = masses[j];

        const dx = massJ.x - massI.x;
        const dy = massJ.y - massI.y;
        const dz = massJ.z - massI.z;

        const distSq = dx * dx + dy * dy + dz * dz;

        f = (g * massJ.m) / (distSq * Math.sqrt(distSq + softeningConstant));

        ax += dx * f;
        ay += dy * f;
        az += dz * f;
      }
    }

    massI.ax = ax;
    massI.ay = ay;
    massI.az = az;
  }
};
		

Мы выполняем проход по всему массиву тел в симуляции и для каждого из них вычисляем влияние на ускорение других тел во вложенном цикле. И соответственно увеличиваем векторы ускорения. Как только выходим из вложенного цикла, обновляем векторы ускорения massI, которые можно затем использовать для вычисления его новых векторов скорости. Теперь мы умеем обновлять векторы положения, скорости и ускорения N-объектного гравитационного моделирования с использованием численного интегрирования.

В текущих вычислениях не хватает единиц измерения. Логично будет выбрать шкалу, которая подходит для рассматриваемых величин, чтобы избежать неуклюжих длинных чисел. В случае с нашей Солнечной системой учёные склонны использовать астрономические единицы для расстояния, солнечную массу для сравнения с другими телами и года для времени. Принимая этот набор единиц, значение гравитационной постоянной g составляет 39,5. Для определения векторов положения и скорости всех тел обратимся к веб-интерфейсу HORIZONS, созданному NASA JPL, где изменим выходную настройку на векторные таблицы, а единицы — на астрономические единицы и дни. По какой-то причине Horizons не измеряет векторы годами в качестве единицы времени. Поэтому мы должны умножить векторы скорости на 365,25 (количество дней в году), чтобы получить векторы скорости, которые согласуются с нашим выбором единиц измерения времени (годы).

Класс JavaScript кажется отличным способом инкапсуляции методов, которые мы написали выше. Сделаем некоторый рефакторинг:

			class nBodyProblem {
  constructor(params) {
    this.g = params.g;
    this.dt = params.dt;
    this.softeningConstant = params.softeningConstant;
    this.masses = params.masses;
  }

  updatePositionVectors() {
    const massesLen = this.masses.length;

    for (let i = 0; i < massesLen; i++) {
      const massI = this.masses[i];

      massI.x += massI.vx * this.dt;
      massI.y += massI.vy * this.dt;
      massI.z += massI.vz * this.dt;
    }

    return this;
  }

  updateVelocityVectors() {
    const massesLen = this.masses.length;

    for (let i = 0; i < massesLen; i++) {
      const massI = this.masses[i];
      massI.vx += massI.ax * this.dt;
      massI.vy += massI.ay * this.dt;
      massI.vz += massI.az * this.dt;
    }
  }

  updateAccelerationVectors() {
    const massesLen = this.masses.length;

    for (let i = 0; i < massesLen; i++) {
      let ax = 0;
      let ay = 0;
      let az = 0;

      const massI = this.masses[i];

      for (let j = 0; j < massesLen; j++) {
        if (i !== j) {
          const massJ = this.masses[j];
          const dx = massJ.x - massI.x;
          const dy = massJ.y - massI.y;
          const dz = massJ.z - massI.z;
          const distSq = dx * dx + dy * dy + dz * dz;

          const f =
            (this.g * massJ.m) /
            (distSq * Math.sqrt(distSq + this.softeningConstant));
          ax += dx * f;
          ay += dy * f;
          az += dz * f;
        }
      }

      massI.ax = ax;
      massI.ay = ay;
      massI.az = az;
    }
    return this;
  }
}
		

Так выглядит намного лучше. Создадим экземпляр класса. Для этого нам нужно указать три константы, а именно гравитационную постоянную (g), шаг по времени моделирования (dt) и постоянную размягчения (softeningConstant). Также нужно заполнить массив объектами (небесными телами). Как только мы сделаем всё это, мы можем создать экземпляр класса nBodyProblem, который назовём innerSolarSystem, поскольку моделирование будет затрагивать внутреннюю часть Солнечной системы.

			const g = 39.5;
const dt = 0.008; // 0,008 года равно 2,92 дня
const softeningConstant = 0.15;

const masses = [{
    name: "Sun", // в качестве единицы массы используем солнечную,
                 // поэтому масса Солнца равна 1
    m: 1,
    x: -1.50324727873647e-6,
    y: -3.93762725944737e-6,
    z: -4.86567877183925e-8,
    vx: 3.1669325898331e-5,
    vy: -6.85489559263319e-6,
    vz: -7.90076642683254e-7
  }
  // Данные по Меркурию, Венере, Земле и Марсу
  // можно найти в контейнере Pen к этому уроку
];

const innerSolarSystem = new nBodyProblem({
  g,
  dt,
  masses: JSON.parse(JSON.stringify(masses)), 
  softeningConstant
});
		

Вас может сбить с толку, казалось бы, ненужный парсинг и строковое представление JSON. Мы передаём данные, содержащиеся в массиве masses, конструктору nBodyProblem, чтобы пользователи могли сбросить симуляцию к исходной точке. Если же передать сам массив в конструктор при создании экземпляра класса, а затем установить значение свойства masses этого экземпляра равным массиву masses, когда пользователь нажмет кнопку сброса, симуляция не вернётся к начальным данным. Состояние тел на конец предыдущего запуска симуляции будет прежним, как и любые другие тела, добавленные пользователем. Чтобы решить эту проблему, нужно передать клон массива masses, когда создаётся экземпляр класса nBodyProblem. Самый простой способ клонирования — это просто парсить строковую версию массива.

Для продвижения симуляции на следующий шаг вызываем:

			innerSolarSystem.updatePositionVectors()
                .updateAccelerationVectors()
                .updateVelocityVectors();
		

Создание визуального отображения небесных тел

Можно было бы представить тела маленькими кружками, созданными с помощью метода arc() в Canvas API, но визуализация траекторий тел в пространстве и времени была бы сложной. Поэтому напишем класс, который будет шаблоном для визуального отображения тел. Создадим круг, который оставляет за собой заранее определённое количество меньших по размеру и поблёкших кружков и передаёт движение и направление. Чем дальше вы удаляетесь от текущей позиции тела, тем меньшие по размеру и более затухающие будут круги. Таким образом, создадим красивую траекторию движения тел.

Конструктор принимает три аргумента:

• контекст рисования для элемента canvas (ctx);
• длину траектории движения (trailLength), представляющую собой количество предыдущих позиций тела, которые след отображает;
• радиус круга (radius), который представляет текущее положение тела.

В конструкторе также инициализируем пустой массив positions, который будет хранить текущие и предыдущие позиции тела, включённые в траекторию движения.

На данном этапе наш класс отображения выглядит так:

			class Manifestation {

  constructor(ctx, trailLength, radius) {
    this.ctx = ctx;
    
    this.trailLength = trailLength;

    this.radius = radius;

    this.positions = [];
  }
  
}
		

Теперь необходимо заполнить массив positions позициями и убедиться, что их хранится не больше, чем указано в свойстве trailLength. Для этого нужно добавить в класс метод, который принимает координаты x и y в качестве аргументов и сохраняет их в массиве, используя метод push(), который добавляет элемент в массив. Это означает, что текущая позиция тела будет последним элементом в массиве positions. Чтобы убедиться, что мы не храним больше позиций, чем указано при создании экземпляра класса, проверяем, превышает ли длина массива positions значение в свойстве trailLength. Если превышает, используем метод shift(), чтобы удалить первый элемент (самая старая сохраненная позиция массива).

			class Manifestation {

  constructor() { /* Код для конструктора описан выше */ }

  storePosition(x, y) {
    this.positions.push({ x, y });

    if (this.positions.length > this.trailLength) 
      this.positions.shift();
  }
		

Напишем метод, который рисует траекторию движения. Он будет принимать два аргумента, а именно положения x и y движущегося тела. Первое, что нужно сделать, это сохранить новую позицию в массиве positions и отбросить всё лишние, хранящиеся в нём. Затем надо перебрать этот массив и нарисовать круг для каждой позиции. Но это по-прежнему выглядит не очень.

Нам нужен масштабный коэффициент, величина которого зависит от удалённости рисуемой позиции от текущей позиции тела. Хорошим способом будет просто разделить индекс круга i на длину массива positions. Например, если количество хранящихся элементов равно 25, элемент с номером 23 в этом массиве получит масштабный коэффициент 23/25 (0,92). Элемент 5 получит масштабный коэффициент 5/25 (0,2). Коэффициент масштабирования уменьшается по мере удаления от текущего положения тела. Обратите внимание, что нам нужно условие, гарантирующее, что масштабный коэффициент текущей позиции устанавливается равным 1 (т. к. этот круг не должен быть блёклым). Учитывая всё это, напишем код для метода draw() в классе Manifestation.

			class Manifestation {

  constructor() { /* Код для конструктора описан выше */ }

  storePosition() { /* Код для storePosition() описан выше */ } 

  draw(x, y) {
    this.storePosition(x, y);

    const positionsLen = this.positions.length;

    for (let i = 0; i < positionsLen; i++) {
      let transparency;
      let circleScaleFactor;

      const scaleFactor = i / positionsLen;

      if (i === positionsLen - 1) {
        transparency = 1;
        circleScaleFactor = 1;
      } else {
        transparency = scaleFactor / 2;
        circleScaleFactor = scaleFactor;
      }

      this.ctx.beginPath();
      this.ctx.arc(
        this.positions[i].x,
        this.positions[i].y,
        circleScaleFactor * this.radius,
        0,
        2 * Math.PI
      );
      this.ctx.fillStyle = `rgb(0, 12, 153, ${transparency})`;

      this.ctx.fill();
    }
  }
  
}
		

Визуализация симуляции

Напишем несколько canvas-шаблонов и свяжем их вместе с гравитационным N-объектным алгоритмом и траекториями движения, чтобы получить анимацию нашей Солнечной системы.

Прежде чем продолжить, вот HTML-код для симулятора:

			<section id="controls-wrapper">
  <label>Масса добавленной планеты</label>
  <select id="masses-list">
    <option value="0.000003003">Земля</option> 
    <option value="0.0009543">Юпитер</option>
    <option value="1">Солнце</option>
    <option value="0.1">Красный карлик</option>
  </select>
  <button id="reset-button">Сброс</button>
</section>
<canvas id="canvas"></canvas>
		

Теперь перейдём к части JavaScript. Для начала нужна ссылка на canvas-элемент, после чего получаем его контекст рисования. Далее устанавливаем размеры. В данном примере установим свойства width и heightcanvas-элемента равными ширине и высоте окна браузера соответственно.

			const canvas = document.querySelector("#canvas");
const ctx = canvas.getContext("2d");

const width = (canvas.width = window.innerWidth);
const height = (canvas.height = window.innerHeight);
		

На данном этапе объявим некоторые константы для анимации:

• радиус круга (radius) — представляет текущее положение тела в пикселях;
• длина следа движения (trailLength) — количество предыдущих позиций, которые включает траектория;
• константа масштаба (scale) — количество пикселей на астрономическую единицу. Земля — это одна астрономическая единица, а Солнце — другая, поэтому, если не ввести этот масштабный коэффициент, наша внутренняя Солнечная система будет выглядеть слишком сжатой.

			const scale = 70;
const radius = 4;
const trailLength = 35;
		

Теперь перейдём к визуальному отображению тел. Написанный ранее класс инкапсулирует поведение этих тел, но также нужно создавать экземпляры класса и работать с этими проявлениями в коде. Наиболее удобный и элегантный способ — заполнить каждый элемент массива masses экземплярами класса Manifestation. Напишем простой метод, который выполняет итерации по этим телам.

			const populateManifestations = masses => {
  masses.forEach(
    mass =>
    (mass["manifestation"] = new Manifestation(
      ctx,
      trailLength,
      radius
    ))
  );
};

populateManifestations(innerSolarSystem.masses);
		

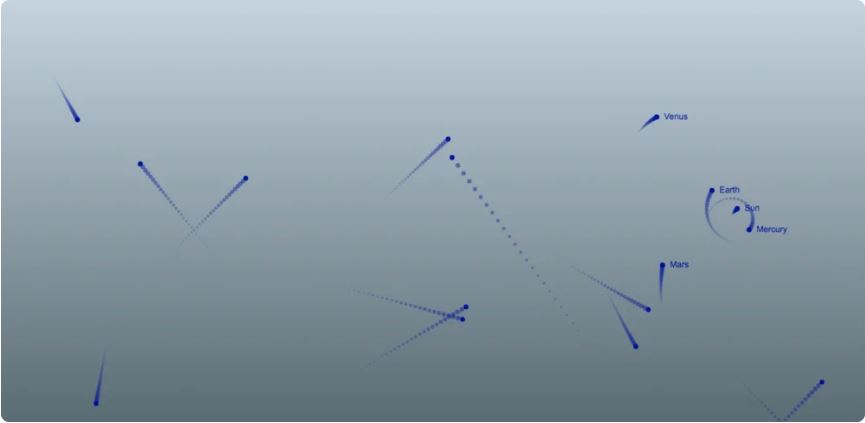
Предполагается, что симулятор должен иметь игровую форму, поэтому вполне можно ожидать, что пользователи будут создавать тела налево и направо и через некоторое время симуляция будет похожа на космический беспорядок. Было бы неплохо предоставить пользователям возможность сбросить симуляцию. Чтобы это сделать, нужно для начала прикрепить обработчик события к кнопке сброса. Затем написать для него callback, который передаёт значение свойства masses объекта innerSolarSystem в клон массива masses. Благодаря тому, что все действия проводились с клоном массива masses, изначальный массив не содержит добавленных после тел. Поэтому вызываем метод populateManifestations(), чтобы всё вернулось к некоторой исходной точке.

			document.querySelector('#reset-button').addEventListener('click', () => {
  innerSolarSystem.masses = JSON.parse(JSON.stringify(masses));
  populateManifestations(innerSolarSystem.masses);       
}, false);
		

Достаточно настроек. Вдохнём немного жизни в симуляцию, написав метод, который с помощью requestAnimationFrame API будет выполнять 60 шагов моделирования в секунду и анимировать движения тел.

Первое, что делает этот метод — продвигает симуляцию на один шаг. Это происходит путём обновления векторов положения, ускорения и скорости тел. Затем выполняется подготовка элемента canvas для следующего цикла анимации (очистка от нарисованных в предыдущем цикле анимации элементов с помощью метода clearRect()).

Далее происходит перебор массива и вызов метода draw() для каждого отображения тела. Если тело имеет имя, также рисуем его в canvas, чтобы пользователь мог видеть, где находятся исходные планеты. Взглянув на код в цикле, вы можете заметить, что значение координаты x нового добавленного тела не становится равна massI, умноженному на масштаб. Вместо этого оно становится равно ширине области просмотра, делённой на (2 + massI), умноженной на масштаб. Это нужно потому, что начало (x = 0, y = 0) системы координат холста задаётся в верхнем левом углу элемента canvas. Поэтому для центрирования моделирования необходимо задавать такое смещение.

После цикла в конце метода animate() вызываем requestAnimationFrame с методом animate() в качестве callback. Затем весь процесс повторяется снова, создавая ещё один кадр. Всё это выполняется очень быстро, создавая видимость движения в симуляции. Но мы кое-что всё-таки упустили. Если запустить приведённый выше код, то вы ничего не увидите. Всё, что нужно сделать, — подтолкнуть Солнечную систему методом animate().

			const animate = () => {
  innerSolarSystem
    .updatePositionVectors()
    .updateAccelerationVectors()
    .updateVelocityVectors();

  ctx.clearRect(0, 0, width, height);

  const massesLen = innerSolarSystem.masses.length;

  for (let i = 0; i < massesLen; i++) {
    const massI = innerSolarSystem.masses[i];

    const x = width / 2 + massI.x * scale;
    const y = height / 2 + massI.y * scale;

    massI.manifestation.draw(x, y);

    if (massI.name) {
      ctx.font = "14px Arial";
      ctx.fillText(massI.name, x + 12, y + 4);
      ctx.fill();
    }
  }

  requestAnimationFrame(animate);
};

animate();
		

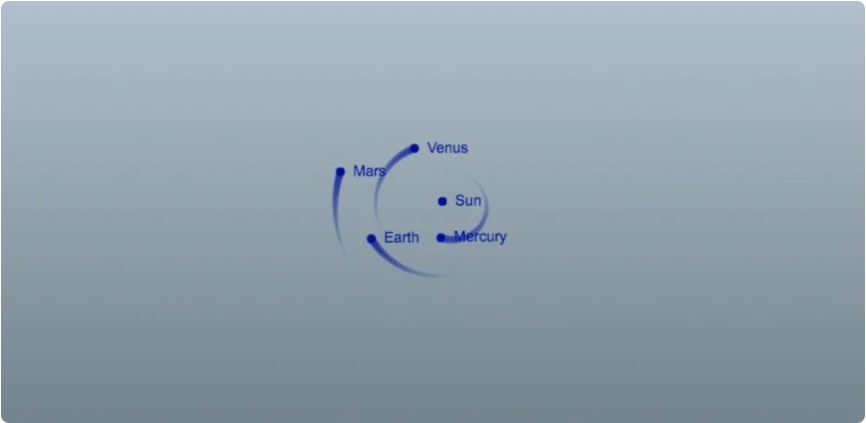
Теперь симулятор ожил. Тела представлены маленькими синими кругами с траекториями движения. Но ещё не реализован механизм добавления пользователем собственных тел с помощью мыши.

Добавление небесных тел в симуляцию

Идея заключается в том, чтобы пользователь имел возможность нарисовать с помощью мышки линию, зажав кнопку и переместив курсор. Направление линии и её длина должны определять направление движения и начальную скорость нового небесного тела соответственно. Новый объект симуляции создаётся как только линия начерчена, а пользователь отпускает зажатую клавишу мыши. Разберёмся, как можно шаг за шагом это реализовать. Код для шагов с первого по шестой располагается выше метода animate(), код для седьмого шага является небольшим дополнением к этому методу.

1. Задаём две переменные, которые будут хранить координаты x и y, где пользователь нажимал кнопку мыши на экране.let mousePressX = 0;let mousePressY = 0;
2. Задаём две переменные, которые хранят координаты x и y текущего положения курсора мыши на экране.let currentMouseX = 0;let currentMouseY = 0;
3. Задаём одну переменную, которая хранит состояние: перемещается мышь или нет. Мышь перетаскивается за время, прошедшее с момента, когда пользователь нажал кнопку мыши, до момента, когда он отпустил её.let dragging = false;
4. Добавляем обработчик mousedown к элементу canvas, записывающий координаты x и y того места, где была нажата мышь, и устанавливает переменную перемещения в значение true.canvas.addEventListener( "mousedown", e => { mousePressX = e.clientX; mousePressY = e.clientY; dragging = true; }, false);
5. Добавляем обработчик mousemove к элементу canvas, записывающий координаты x и y текущего положения курсора мыши.canvas.addEventListener( "mousemove", e => { currentMouseX = e.clientX; currentMouseY = e.clientY; }, false);
6. Добавляем слушателя mouseup к элементу canvas, который устанавливает переменную перетаскивания в false, и помещает новый объект (небесное тело) в массив innerSolarSystem.masses. Координаты нажатия клавиши выражаются векторами позиции, разделёнными на значение переменной масштаба.
   ­
   Если не поделить эти векторы на переменную масштаба, добавленные тела окажутся за пределами Солнечной системы. Вектор положения z установлен на ноль, как и вектор скорости z. Вектор скорости x установлен на координату x, где мышь была отпущена, минус координата x, где мышь была нажата, а затем всё это разделено на 35. 35 — это магическое число, которое просто присутствует, чтобы скорости добавляемых объектов были разумными. Та же процедура производится и для вектора скорости y. Масса тела (m) задаётся пользователем с помощью элемента select, заполненного ранее массами некоторых известных небесных объектов в разметке HTML. И, наконец, заполняем объект (небесное тело) экземпляром класса Manifestation, чтобы пользователь мог видеть его на экране;const massesList = document.querySelector("#masses-list");canvas.addEventListener( "mouseup", e => { const x = (mousePressX - width / 2) / scale; const y = (mousePressY - height / 2) / scale; const z = 0; const vx = (e.clientX - mousePressX) / 35; const vy = (e.clientY - mousePressY) / 35; const vz = 0; innerSolarSystem.masses.push({ m: parseFloat(massesList.value), x, y, z, vx, vy, vz, manifestation: new Manifestation(ctx, trailLength, radius) }); dragging = false; }, false);
7. В функции animate() после цикла рисования и перед вызовом requestAnimationFrame проверяем, не перетаскивается ли мышь. Если это так, нарисуем линию между позицией нажатия мыши и текущей позицией курсора.const animate = () => { // Предшествующий код в методе animate() вплоть до цикла, // где рисуются изображения небесных тел if (dragging) { ctx.beginPath(); ctx.moveTo(mousePressX, mousePressY); ctx.lineTo(currentMouseX, currentMouseY); ctx.strokeStyle = "red"; ctx.stroke(); } requestAnimationFrame(animate);};

Ограничение симуляции

Вероятно вы заметили, что добавленные тела имеют тенденцию выходить за пределы моделируемой Солнечной системы, что очень не желательно. Естественное решение этой проблемы — ограничить симуляцию. Когда тело достигнет края холста, оно должно отскочить назад. Звучит довольно сложно, но, к счастью, сделать это легко. В конце цикла, где объекты перебираются и рисуются методом animate(), нужно добавить два условия:

• проверяем, находится ли тело за пределами области просмотра на оси x;
• такое же условие для оси у.

Если тело находится вне области просмотра на оси x, обращаем его вектор скорости так, чтобы он возвращался обратно в область просмотра. Аналогично для оси y. При этих двух условиях метод animate() будет выглядеть так:

			const animate = () => {
  // Продвижение симуляции на один шаг и очищение холста

  for (let i = 0; i < massesLen; i++) {
    // Предшествующий код цикла
    if (x < radius || x > width - radius) massI.vx = -massI.vx;
    if (y < radius || y > height - radius) massI.vy = -massI.vy;
  }
  requestAnimationFrame(animate);
};
		

Заключение

Люди склонны думать об орбитальной механике, как о чём-то, находящемся за пределами их понимания. Правда в том, что эта механика следует очень простому и элегантному набору правил. Немного JavaScript, математики и физики из средней школы, и вы смогли реконструировать внутреннюю часть Солнечной системы с довольно неплохой точностью. С помощью этого симулятора вы можете ответить на вопросы типа: «Что произошло, если бы появилась звезда с массой Солнца в нашей солнечной системе?», — или больше узнать о взаимосвязи между расстоянием тела от Солнца и его скоростью.

Если вам понравился этот материал и вы хотите посмотреть больше проектов по космосу и физике, загляните в этот репозиторий, а также посмотрите проект «Гармония сфер».