Алгоритмы и структуры данных для начинающих: множества

Множество — это коллекция, которая реализует основные математические операции над множествами: пересечения (intersection), объединение (union), разность (difference) и симметрическая разность (symmetric difference). Каждый из алгоритмов мы разберем в соответствующем разделе.

Также смотрите другие материалы этой серии: бинарное дерево, стеки и очереди, динамический массив, связный список, оценка сложности алгоритма и сортировка.

Множество

В математике множества — это коллекции объектов, у которых есть что-то общее. Например, мы можем объявить множество четных положительных целых чисел:

Или множество нечетных положительных целых:

В этих двух множествах нет общих элементов. Давайте теперь посмотрим на множество делителей числа 100:

Теперь мы можем узнать, какие делители числа 100 — нечетные, просто глядя на множество нечетных чисел и на множество делителей и выбирая те из чисел, которые присутствуют в обоих. Мы также можем ответить на вопрос: «Какие нечетные числа не являются делителями ста?» или «Какие положительные целые, четные или нечетные, не являются делителями ста?».

На первый взгляд это кажется не очень полезным, но это искусственный пример. Предположим, что у нас есть множество всех работников предприятия и множество работников, прошедших ежемесячную проверку. Тогда мы с легкостью сможем ответить на вопрос: «Кто из работников не прошел проверку?».

Мы также можем добавить различные множества и построить более сложный запрос, например: «Кто из штатных работников отдела продаж, имеющих корпоративную кредитную карточку, не прошел обязательный курс повышения квалификации?».

Класс Set

Класс Set реализует интерфейс IEnumerable и принимает аргумент типа, который является наследником IComparable, так как для работы алгоритмов нужна проверка элементов на равенство.

Элементы нашего множества будут храниться в экземпляре стандартного класса .NET List, но на практике для хранения обычно используются древовидные структуры, например, двоичное дерево поиска. Выбор внутреннего представления будет влиять на сложность алгоритмов работы с множеством. К примеру, при использовании списка метод Contains будет выполняться за O(n) времени, в то время как множество, реализованное с помощью дерева, будет работать в среднем за O(log n) времени.

Кроме методов для работы с множеством класс Set также имеет конструктор, который принимает IEnumerable с начальными элементами.

Метод Add

• Поведение: Добавляет элементы в множество. Если элемент уже присутствует в множестве, бросается исключение InvalidOperationException.
• Сложность: O(n)

При реализации метода Add необходимо решить, будем ли мы разрешать дублирующиеся элементы. К примеру, если у нас есть мнжество:

Если пользователь попытается добавить число 3, в результате получится:

В некоторых случаях это допустимо, но в нашей реализации мы не будем поддерживать дубликаты. Если представить, например, множество студентов колледжа, было бы нелогичным добавлять в него одного и того же студента дважды. На самом деле, попытка добавить элемент, который уже присутствует — скорее всего ошибка, и наша реализация класса Set воспринимает ее именно так.

Метод Add использует метод Contains, который будет рассмотрен далее.

Метод AddRange

• Поведение: Добавляет несколько элементов в множество. Если какой-либо из добавляемых элементов присутствует в множестве, или в добавляемых элементах есть дублирующиеся, выбрасывается исключение InvalidOperationException.
• Сложность: O(m·n), где m — количество вставляемых элементов и n — количество элементов множества.

Метод Remove

• Поведение: Удаляет указанный элемент из множества и возвращает true. В случае, если элемента нет, возвращает false.
• Сложность: O(n)

Метод Contains

• Поведение: Возвращает true, если множество содержит указанный элемент. В противном случае возвращает false.
• Сложность: O(n)

Метод Count

• Поведение: Возвращает количество элементов множества или 0, если множество пусто.
• Сложность: O(1)

Метод GetEnumerator

• Поведение: Возвращает итератор для перебора элементов множества.
• Сложность: Получение итератора — O(1), обход элементов множества — O(n).

Алгоритмы

Метод Union

• Поведение: Возвращает множество, полученное операцией объединения его с указанным.
• Сложность: O(m·n), где m и n — количество элементов переданного и текущего множеств соответственно.

Объединение множеств — это множество, которое содержит элементы, присутствующие хотя бы в одном из двух.

Например, есть два множества (выделены красным):

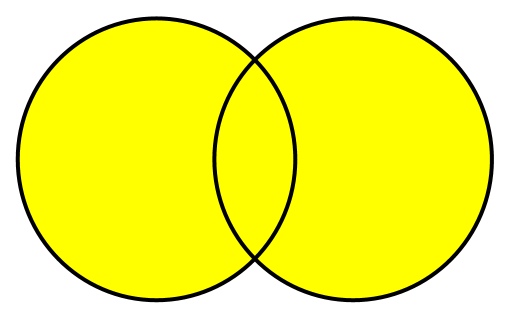
При операции объединения выбираются элементы обоих множеств. Если элемент присутствует в обоих множествах, берется только одна его копия. Объединение двух множеств показано желтым цветом.

Такая диаграмма, наглядно показывающая операции над множествами, называется диаграммой Венна.

Другой пример с использованием множеств целых чисел:

Метод Intersection

• Поведение: Возвращает множество, полученное операцией пересечения его с указанным.
• Сложность: O(m·n), где m и n — количество элементов переданного и текущего множеств соответственно.

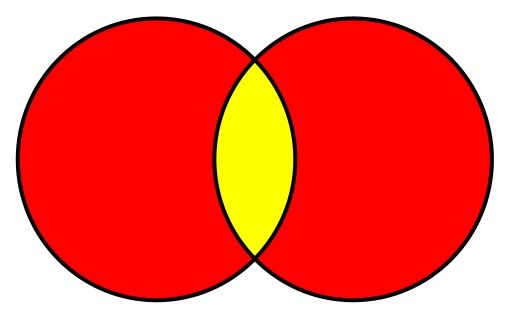
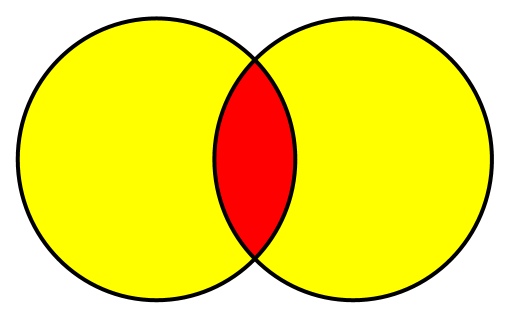
Пересечение множеств содержит только те элементы, которые есть в обоих множествах. Используя диаграмму Венна, пересечение можно изобразить так:

Или, используя целые числа:

Метод Difference

• Поведение: Возвращает множество, являющееся разностью текущего с указанным.
• Сложность: O(m·n), где m и n — количество элементов переданного и текущего множеств соответственно.

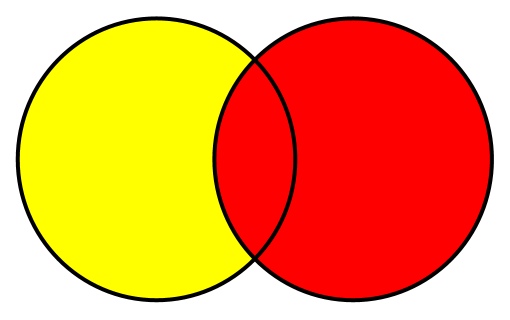
Разность множеств — это все элементы, которые содержатся в одном множестве (том, у которого вызывается метод), но не содержатся в другом (том, которое передается аргументом). Диаграмма Венна для разности множеств будет выглядеть так:

Или, используя целые числа:

Метод Symmetric Difference

• Поведение: Возвращает множество, являющееся симметрической разностью текущего с указанным.
• Сложность: O(m·n), где m и n — количество элементов переданного и текущего множеств соответственно.

Симметрическая разность — это все элементы, которые содержатся только в одном из рассматриваемых множеств. Диаграмма Венна для симметрической разности будет выглядеть так:

Или, используя целые числа:

Вы, возможно, заметили, что симметрическая разность — это «пересечение наоборот». Учитывая это, давайте попробуем найти ее, используя уже имеющиеся операции.

Итак, мы хотим получить множество, которое содержит все элементы из двух множеств, за исключением тех, которые есть в обоих. Другими словами, мы хотим получить разность объединения двух множеств и их пересечения.

Или, если рассматривать по шагам:

Что дает нам нужный результат: [1, 2, 5, 6].

Метод IsSubset

Вы, возможно, интересуетесь, почему мы не добавили метод IsSubset, который проверяет, содержится ли одно множество целиком в другом. Например:

В то время, как:

Дело в том, что эту проверку можно провести, используя имещиеся методы. К примеру:

Пустое множество в результате говорит нам о том, что все элементы первого множества содержатся во втором, а значит, первое является подмножеством второго. Другой способ проверить это:

Если в результате мы получим множество с таким же количеством элементов, что и изначальное, значит, оно является подмножеством второго.

В общем случае, конечно, класс Set может иметь метод IsSubset (который может быть реализован более эффективно). Однако стоит помнить, что это уже не какая-то новая возможность, а просто другое применение существующих.

Продолжение следует

На этом все, а в следующий раз мы перейдем к заключительной теме этого цикла статей — алгоритмам сортировки.

Перевод статьи «The Set Collection»