Алгоритмы и структуры данных для начинающих: двоичное дерево поиска

До сих пор мы рассматривали структуры данных, данные в которых располагаются линейно. В связном списке — от первого узла к единственному последнему. В динамическом массиве — в виде непрерывного блока.

В этой части мы рассмотрим совершенно новую структуру данных — дерево. А точнее, двоичное (бинарное) дерево поиска (binary search tree). Бинарное дерево поиска имеет структуру дерева, но элементы в нем расположены по определенным правилам.

Также смотрите другие материалы этой серии: стеки и очереди, динамический массив, связный список, оценка сложности алгоритма, сортировка и множества.

Для начала мы рассмотрим обычное дерево.

Деревья

Дерево — это структура, в которой у каждого узла может быть ноль или более подузлов — «детей». Например, дерево может выглядеть так:

Это дерево показывает структуру компании. Узлы представляют людей или подразделения, линии — связи и отношения. Дерево — это самый эффективный способ представления и хранения такой информации.

Дерево на картинке выше очень простое. Оно отражает только отношение родства категорий, но не накладывает никаких ограничений на свою структуру. У генерального директора может быть как один непосредственный подчиненный, так и несколько или ни одного. На рисунке отдел продаж находится левее отдела маркетинга, но порядок на самом деле не имеет значения. Единственное ограничение дерева — каждый узел может иметь не более одного родителя. Самый верхний узел (совет директоров, в нашем случае) родителя не имеет. Этот узел называется «корневым», или «корнем».

Вопросы о деревьях задают даже на собеседовании в Apple.

Двоичное дерево поиска

Двоичное дерево поиска похоже на дерево из примера выше, но строится по определенным правилам:

• У каждого узла не более двух детей.
• Любое значение меньше значения узла становится левым ребенком или ребенком левого ребенка.
• Любое значение больше или равное значению узла становится правым ребенком или ребенком правого ребенка.

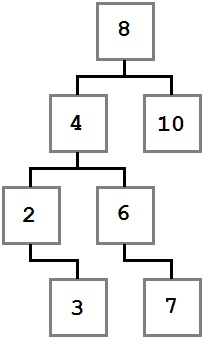
Давайте посмотрим на дерево, построенное по этим правилам:

Обратите внимание, как указанные ограничения влияют на структуру дерева. Каждое значение слева от корня (8) меньше восьми, каждое значение справа — больше либо равно корню. Это правило применимо к любому узлу дерева.

Учитывая это, давайте представим, как можно построить такое дерево. Поскольку вначале дерево было пустым, первое добавленное значение — восьмерка — стало его корнем.

Мы не знаем точно, в каком порядке добавлялись остальные значения, но можем представить один из возможных путей. Узлы добавляются методом Add, который принимает добавляемое значение.

			BinaryTree tree = new BinaryTree();
tree.Add(8);
tree.Add(4);
tree.Add(2);
tree.Add(3);
tree.Add(10);
tree.Add(6);
tree.Add(7);
		

Рассмотрим подробнее первые шаги.

В первую очередь добавляется 8. Это значение становится корнем дерева. Затем мы добавляем 4. Поскольку 4 меньше 8, мы кладем ее в левого ребенка, согласно правилу 2. Поскольку у узла с восьмеркой нет детей слева, 4 становится единственным левым ребенком.

После этого мы добавляем 2. 2 меньше 8, поэтому идем налево. Так как слева уже есть значение, сравниваем его со вставляемым. 2 меньше 4, а у четверки нет детей слева, поэтому 2 становится левым ребенком 4.

Затем мы добавляем тройку. Она идет левее 8 и 4. Но так как 3 больше, чем 2, она становится правым ребенком 2, согласно третьему правилу.

Последовательное сравнение вставляемого значения с потенциальным родителем продолжается до тех пор, пока не будет найдено место для вставки, и повторяется для каждого вставляемого значения до тех пор, пока не будет построено все дерево целиком.

Класс BinaryTreeNode

Класс BinaryTreeNode представляет один узел двоичного дерева. Он содержит ссылки на левое и правое поддеревья (если поддерева нет, ссылка имеет значение null), данные узла и метод IComparable.CompareTo для сравнения узлов. Он пригодится для определения, в какое поддерево должен идти данный узел. Как видите, класс BinaryTreeNode очень простой:

			class BinaryTreeNode : IComparable
    where TNode : IComparable
{
    public BinaryTreeNode(TNode value)
    {
        Value = value;
    }
 
    public BinaryTreeNode Left { get; set; }
    public BinaryTreeNode Right { get; set; }
    public TNode Value { get; private set; }
 
    /// 
    /// Сравнивает текущий узел с данным.
    /// 
    /// Сравнение производится по полю Value.
    /// Метод возвращает 1, если значение текущего узла больше,
    /// чем переданного методу, -1, если меньше и 0, если они равны
    public int CompareTo(TNode other)
    {
        return Value.CompareTo(other);
    }
}
		

Класс BinaryTree

Класс BinaryTree предоставляет основные методы для манипуляций с данными: вставка элемента (Add), удаление (Remove), метод Contains для проверки, есть ли такое значение в дереве, несколько методов для обхода дерева различными способами, метод Count и Clear.

Кроме того, в классе есть ссылка на корневой узел дерева и поле с общим количеством узлов.

			public class BinaryTree : IEnumerable
    where T : IComparable
{
    private  BinaryTreeNode _head;
    private int _count;
 
    public void Add(T value)
    {
        throw new NotImplementedException();
    }
 
    public bool Contains(T value)
    {
        throw new NotImplementedException();
    }
 
    public bool Remove(T value)
    {
        throw new NotImplementedException();
    }
 
    public void PreOrderTraversal(Action action)
    {
        throw new NotImplementedException();
    }
 
    public void PostOrderTraversal(Action action)
    {
        throw new NotImplementedException();
    }
 
    public void InOrderTraversal(Action action)
    {
        throw new NotImplementedException();
    }
 
    public IEnumerator GetEnumerator()
    {
        throw new NotImplementedException();
    }
 
    System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator()
    {
        throw new NotImplementedException();
    }
 
    public void Clear()
    {
        throw new NotImplementedException();
    }
 
    public int Count
    {
        get;
    }
}
		

Метод Add

• Поведение: Добавляет элемент в дерево на корректную позицию.
• Сложность: O(log n) в среднем; O(n) в худшем случае.

Добавление узла не представляет особой сложности. Оно становится еще проще, если решать эту задачу рекурсивно. Есть всего два случая, которые надо учесть:

1. Дерево пустое.
2. Дерево не пустое.

Если дерево пустое, мы просто создаем новый узел и добавляем его в дерево. Во втором случае мы сравниваем переданное значение со значением в узле, начиная от корня. Если добавляемое значение меньше значения рассматриваемого узла, повторяем ту же процедуру для левого поддерева. В противном случае — для правого.

			public void Add(T value)
{
//Случай 1: Если дерево пустое, просто создаем корневой узел.
    if (_head == null)
    {
        _head = new BinaryTreeNode(value);
    }
//Случай 2: Дерево не пустое => 
//ищем правильное место для вставки.
    else
    {
        AddTo(_head, value);
    }
 
    _count++;
}
 
//Рекурсивная ставка.
private void AddTo(BinaryTreeNode node, T value)
{
//Случай 1: Вставляемое значение меньше значения узла
    if (value.CompareTo(node.Value) < 0)
    {
//Если нет левого поддерева, добавляем значение в левого ребенка,
        if (node.Left == null)
        {
            node.Left = new BinaryTreeNode(value);
        }
        else
        {
//в противном случае повторяем для левого поддерева.
            AddTo(node.Left, value);
        }
    }
//Случай 2: Вставляемое значение больше или равно значению узла.
    else
    {
//Если нет правого поддерева, добавляем значение в правого ребенка,
        if (node.Right == null)
        {
            node.Right = new BinaryTreeNode(value);
        }
        else
        {
//в противном случае повторяем для правого поддерева.
            AddTo(node.Right, value);
        }
    }
}
		

Метод Remove

• Поведение: Удаляет первый узел с заданным значением.
• Сложность: O(log n) в среднем; O(n) в худшем случае.

Удаление узла из дерева — одна из тех операций, которые кажутся простыми, но на самом деле таят в себе немало подводных камней.

В целом, алгоритм удаления элемента выглядит так:

• Найти узел, который надо удалить.
• Удалить его.

Первый шаг достаточно простой. Мы рассмотрим поиск узла в методе Contains ниже. После того, как мы нашли узел, который необходимо удалить, у нас возможны три случая.

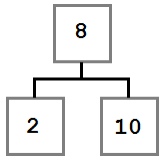
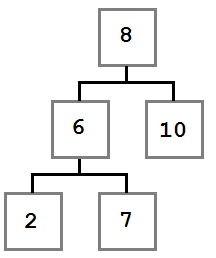
Случай 1: У удаляемого узла нет правого ребенка.

В этом случае мы просто перемещаем левого ребенка (при его наличии) на место удаляемого узла. В результате дерево будет выглядеть так:

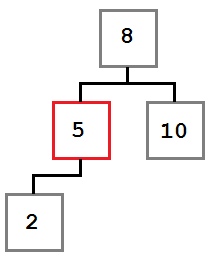
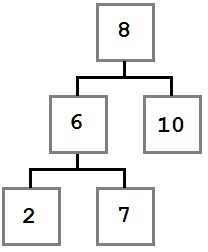
Случай 2: У удаляемого узла есть только правый ребенок, у которого, в свою очередь нет левого ребенка.

В этом случае нам надо переместить правого ребенка удаляемого узла (6) на его место. После удаления дерево будет выглядеть так:

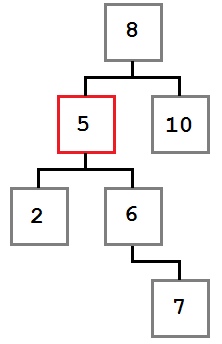
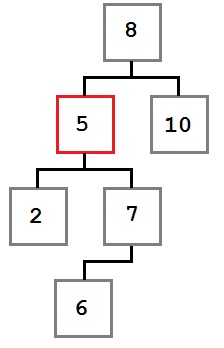
Случай 3: У удаляемого узла есть первый ребенок, у которого есть левый ребенок.

В этом случае место удаляемого узла занимает крайний левый ребенок правого ребенка удаляемого узла.

Давайте посмотрим, почему это так. Мы знаем о поддереве, начинающемся с удаляемого узла следующее:

• Все значения справа от него больше или равны значению самого узла.
• Наименьшее значение правого поддерева — крайнее левое.

Мы дожны поместить на место удаляемого узел со значением, меньшим или равным любому узлу справа от него. Для этого нам необходимо найти наименьшее значение в правом поддереве. Поэтому мы берем крайний левый узел правого поддерева.

После удаления узла дерево будет выглядеть так:

Теперь, когда мы знаем, как удалять узлы, посмотрим на код, который реализует этот алгоритм.

Отметим, что метод FindWithParent (см. метод Contains) возвращает найденный узел и его родителя, поскольку мы должны заменить левого или правого ребенка родителя удаляемого узла.

Мы, конечно, можем избежать этого, если будем хранить ссылку на родителя в каждом узле, но это увеличит расход памяти и сложность всех алгоритмов, несмотря на то, что ссылка на родительский узел используется только в одном.

			public bool Remove(T value)
{
    BinaryTreeNode current, parent;
 
    // Находим удаляемый узел.
    current = FindWithParent(value, out parent);
 
    if (current == null)
    {
        return false;
    }
 
    _count--;
 
//Случай 1: Если нет детей справа,
//левый ребенок встает на место удаляемого.
    if (current.Right == null)
    {
        if (parent == null)
        {
            _head = current.Left;
        }
        else
        {
            int result = parent.CompareTo(current.Value);
            if (result > 0)
            {
//Если значение родителя больше текущего,
//левый ребенок текущего узла становится левым ребенком родителя.
                parent.Left = current.Left;
            }
            else if (result < 0) {
//Если значение родителя меньше текущего,
// левый ребенок текущего узла становится правым ребенком родителя.
               parent.Right = current.Left;
             }
         }
    }
//Случай 2: Если у правого ребенка нет детей слева
//то он занимает место удаляемого узла.
            else if (current.Right.Left == null) {
               current.Right.Left = current.Left;
               if (parent == null) {
                 _head = current.Right;
               } else {
                 int result = parent.CompareTo(current.Value);
                 if (result > 0)
            {
//Если значение родителя больше текущего,
//правый ребенок текущего узла становится левым ребенком родителя.
                parent.Left = current.Right;
            }
            else if (result < 0) {
//Если значение родителя меньше текущего,
// правый ребенок текущего узла становится правым ребенком родителя.
               parent.Right = current.Right;
            }
       }
   }
//Случай 3: Если у правого ребенка есть дети слева,
//крайний левый ребенок 
//из правого поддерева заменяет удаляемый узел.
            else {
//Найдем крайний левый узел.
               BinaryTreeNode leftmost = current.Right.Left;
               BinaryTreeNode leftmostParent = current.Right;
               while (leftmost.Left != null) {
                  leftmostParent = leftmost; leftmost = leftmost.Left;
               }
//Левое поддерево родителя становится правым поддеревом
//крайнего левого узла.
               leftmostParent.Left = leftmost.Right;
//Левый и правый ребенок текущего узла становится левым
//и правым ребенком крайнего левого. leftmost.
               Left = current.Left;
               leftmost.Right = current.Right;
               if (parent == null) {
                  _head = leftmost;
               } else {
                  int result = parent.CompareTo(current.Value);
                  if (result > 0)
            {
//Если значение родителя больше текущего,
//крайний левый узел становится левым ребенком родителя.
                parent.Left = leftmost;
            }
            else if (result < 0)
            {
//Если значение родителя меньше текущего,
//крайний левый узел становится правым ребенком родителя.
                parent.Right = leftmost;
            }
        }
    }
 
    return true;
}
		

Метод Contains

• Поведение: Возвращает true если значение содержится в дереве. В противном случает возвращает false.
• Сложность: O(log n) в среднем; O(n) в худшем случае.

Метод Contains выполняется с помощью метода FindWithParent, который проходит по дереву, выполняя в каждом узле следующие шаги:

1. Если текущий узел null, вернуть null.
2. Если значение текущего узла равно искомому, вернуть текущий узел.
3. Если искомое значение меньше значения текущего узла, установить левого ребенка текущим узлом и перейти к шагу 1.
4. В противном случае, установить правого ребенка текущим узлом и перейти к шагу 1.

Поскольку Contains возвращает булево значение, оно определяется сравнением результата выполнения FindWithParent с null. Если FindWithParent вернул непустой узел, Contains возвращает true.

Метод FindWithParent также используется в методе Remove.

			public bool Contains(T value)
{
//Поиск узла осуществляется другим методом.
    BinaryTreeNode parent;
    return FindWithParent(value, out parent) != null;
}
  
//Находит и возвращает первый узел с заданным значением.
//Если значение не найдено, возвращает null.
//Также возвращает родителя найденного узла (или null)
//для использования в методе Remove. 
private BinaryTreeNode FindWithParent(T value,
                            out BinaryTreeNode parent)
{
//Попробуем найти значение в дереве.
    BinaryTreeNode current = _head;
    parent = null;
 
//До тех пор, пока не нашли...
    while (current != null)
    {
        int result = current.CompareTo(value);
 
        if (result > 0)
        {
//Если искомое значение меньше, идем налево.
            parent = current;
            current = current.Left;
        }
        else if (result < 0)
        {
//Если искомое значение больше, идем направо.
            parent = current;
            current = current.Right;
        }
        else
        {
//Если равны, то останавливаемся
            break;
        }
    }
 
    return current;
}
		

Метод Count

• Поведение: Возвращает количество узлов дерева или 0, если дерево пустое.
• Сложность: O(1)

Это поле инкрементируется методом Add и декрементируется методом Remove.

			>public int Count
{
    get
    {
        return _count;
    }
}
		

Метод Clear

• Поведение: Удаляет все узлы дерева.
• Сложность: O(1)

			public void Clear()
{
    _head = null;
    _count = 0;
}
		

Обход деревьев

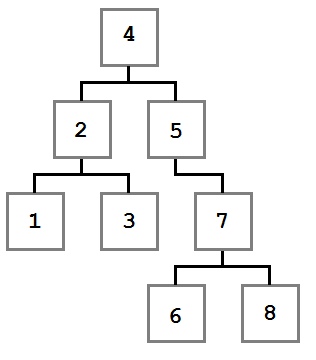
Обходы дерева — это семейство алгоритмов, которые позволяют обработать каждый узел в определенном порядке. Для всех алгоритмов обхода ниже в качестве примера будет использоваться следующее дерево:

Методы обхода в примерах будут принимать параметр Action<T>, который определяет действие, поизводимое над каждым узлом.

Также, кроме описания поведения и алгоритмической сложности метода будет указываться порядок значений, полученный при обходе.

Метод Preorder (или префиксный обход)

• Поведение: Обходит дерево в префиксном порядке, выполняя указанное действие над каждым узлом.
• Сложность: O(n)
• Порядок обхода: 4, 2, 1, 3, 5, 7, 6, 8

При префиксном обходе алгоритм получает значение текущего узла перед тем, как перейти сначала в левое поддерево, а затем в правое. Начиная от корня, сначала мы получим значение 4. Затем таким же образом обходятся левый ребенок и его дети, затем правый ребенок и все его дети.

Префиксный обход обычно применяется для копирования дерева с сохранением его структуры.

			public void PreOrderTraversal(Action action)
{
    PreOrderTraversal(action, _head);
}
 
private void PreOrderTraversal(Action action, BinaryTreeNode node)
{
    if (node != null)
    {
        action(node.Value);
        PreOrderTraversal(action, node.Left);
        PreOrderTraversal(action, node.Right);
    }
}
		

Метод Postorder (или постфиксный обход)

• Поведение: Обходит дерево в постфиксном порядке, выполняя указанное действие над каждым узлом.
• Сложность: O(n)
• Порядок обхода: 1, 3, 2, 6, 8, 7, 5, 4

При постфиксном обходе мы посещаем левое поддерево, правое поддерево, а потом, после обхода всех детей, переходим к самому узлу.

Постфиксный обход часто используется для полного удаления дерева, так как в некоторых языках программирования необходимо убирать из памяти все узлы явно, или для удаления поддерева. Поскольку корень в данном случае обрабатывается последним, мы, таким образом, уменьшаем работу, необходимую для удаления узлов.

			public void PostOrderTraversal(Action action)
{
    PostOrderTraversal(action, _head);
}
 
private void PostOrderTraversal(Action action, BinaryTreeNode node)
{
    if (node != null)
    {
        PostOrderTraversal(action, node.Left);
        PostOrderTraversal(action, node.Right);
        action(node.Value);
    }
}
		

Метод Inorder (или инфиксный обход)

• Поведение: Обходит дерево в инфиксном порядке, выполняя указанное действие над каждым узлом.
• Сложность: O(n)
• Порядок обхода: 1, 2, 3, 4, 5, 6, 7, 8

Инфиксный обход используется тогда, когда нам надо обойти дерево в порядке, соответствующем значениям узлов. В примере выше в дереве находятся числовые значения, поэтому мы обходим их от самого маленького до самого большого. То есть от левых поддеревьев к правым через корень.

В примере ниже показаны два способа инфиксного обхода. Первый — рекурсивный. Он выполняет указанное действие с каждым узлом. Второй использует стек и возвращает итератор для непосредственного перебора.

			Public void InOrderTraversal(Action action)
{
    InOrderTraversal(action, _head);
}
 
private void InOrderTraversal(Action action, BinaryTreeNode node)
{
    if (node != null)
    {
        InOrderTraversal(action, node.Left);
 
        action(node.Value);
 
        InOrderTraversal(action, node.Right);
    }
}
 
public IEnumerator InOrderTraversal()
{
// Это нерекурсивный алгоритм.
// Он использует стек для того, чтобы избежать рекурсии.
    if (_head != null)
    {
// Стек для сохранения пропущенных узлов.
        Stack stack = new Stack();
 
        BinaryTreeNode current = _head;

// Когда мы избавляемся от рекурсии, нам необходимо
// запоминать, в какую стороны мы должны двигаться.
        bool goLeftNext = true;
 
// Кладем в стек корень.
        stack.Push(current);
 
        while (stack.Count > 0)
        {
// Если мы идем налево...
            if (goLeftNext)
            {
// Кладем все, кроме самого левого узла на стек.
// Крайний левый узел мы вернем с помощю yield.
                while (current.Left != null)
                {
                    stack.Push(current);
                    current = current.Left;
                }
            }
 
// Префиксный порядок: left->yield->right.
            yield return current.Value;
 
// Если мы можем пойти направо, идем.
            if (current.Right != null)
            {
                current = current.Right;
 
// После того, как мы пошли направо один раз,
// мы должным снова пойти налево.
                goLeftNext = true;
            }
            else
            {
// Если мы не можем пойти направо, мы должны достать родительский узел
// со стека, обработать его и идти в его правого ребенка.
                current = stack.Pop();
                goLeftNext = false;
            }
        }
    }
}
		

Метод GetEnumerator

• Поведение: Возвращает итератор для обхода дерева инфиксным способом.
• Сложность: Получение итератора — O(1). Обход дерева — O(n).

			public IEnumerator GetEnumerator()
{
    return InOrderTraversal();
}
 
System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator()
{
    return GetEnumerator();
}
		

Продолжение следует

На этом мы заканчивает пятую часть руководства по алгоритмам и структурам данных. В следующей статье мы рассмотрим множества (Set).

Перевод статьи «The Binary Search Tree»