ТОП-15 алгоритмов, которые реально нужны на бэкенде

Алгоритмы — не просто абстрактная теория из учебников, а основа работы любого бэкенда. От поиска данных до оптимизации загрузки — правильный выбор алгоритмов делает систему быстрой, надёжной и масштабируемой. В этой статье — десятка действительно полезных алгоритмов, без которых не обходится ни один серьёзный сервер.

Алгоритмы поиска

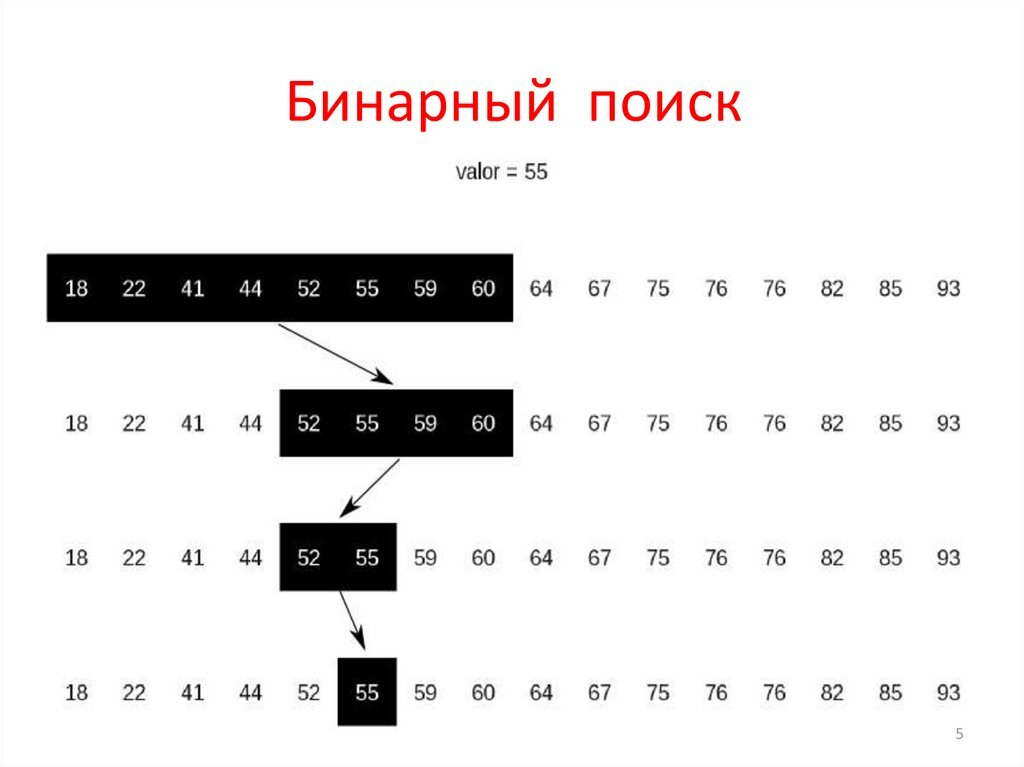
Бинарный поиск: быстрое нахождение элемента в отсортированном массиве

Бинарный поиск — один из самых быстрых способов файндинга элемента массива в backend разработке. Если в линейном поиске все проверяется поэтапно, то в бинарном количество проверок уменьшается за счёт «располовинивания» массива на каждом этапе поиска.

Как работает бинарный поиск:

1. Устанавливаются индексы начала и конца массива;
2. Находится индекс среднего элемента;
3. Если средний элемент равен значению, поиск завершается;
4. Если элемент меньше среднего, поиск продолжается в левой половине массива, а если больше — в правой;
5. И так до тех пор, пока не будет найден элемент.

Бинарный поиск имеет сложность O(log n). Это означает, что сложность растёт логарифмически.

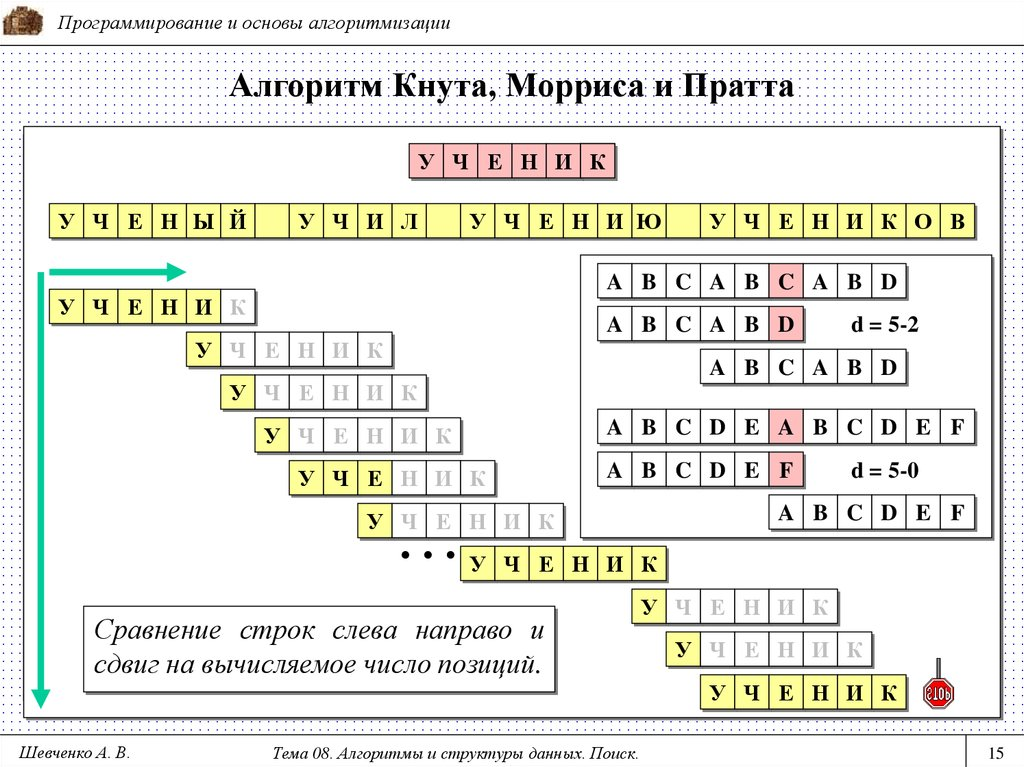
Поиск подстроки: алгоритмы KMP и Rabin-Karp

Поиск текста внутри текста нужен, например, в обработке данных логов.

Алгоритм Кнута-Морриса-Пратта (KMP) был создан для поиска подстрок с предварительной обработкой шаблона.

• Сначала создаётся таблица префиксов, которая выявляет сдвиги шаблона при несовпадении;
• А затем эта же таблица используется для увеличения количества позиций сдвига во время поиска подстроки в тексте.

Алгоритм KMP имеет сложность O(n + m), где n — длина текста, m — длина шаблона. А значит, сложность растёт линейно, в зависимости от длины текста и длины шаблона.

Алгоритм Рабина-Карпа создан для поиска подстроки через хеширование.

• Сначала определяются хеш-коды для шаблона и для каждой подстроки текста той же длины;
• Далее хеши сравниваются. При их совпадении проводится дополнительное сравнение символов;
• В конечном итоге хеш-код обновляется при переходе к следующей позиции текста.

Рабин-Карп нужен, если у вас есть много шаблонов для поиска одновременно — здесь работает параллельное вычисление.

Алгоритмы сортировки

Алгоритмы сортировки помогают в оптимизации данных в backendе. Они снижают время обработки массивов данных. А это особенно важно при высоких нагрузках и больших объёмах информации.

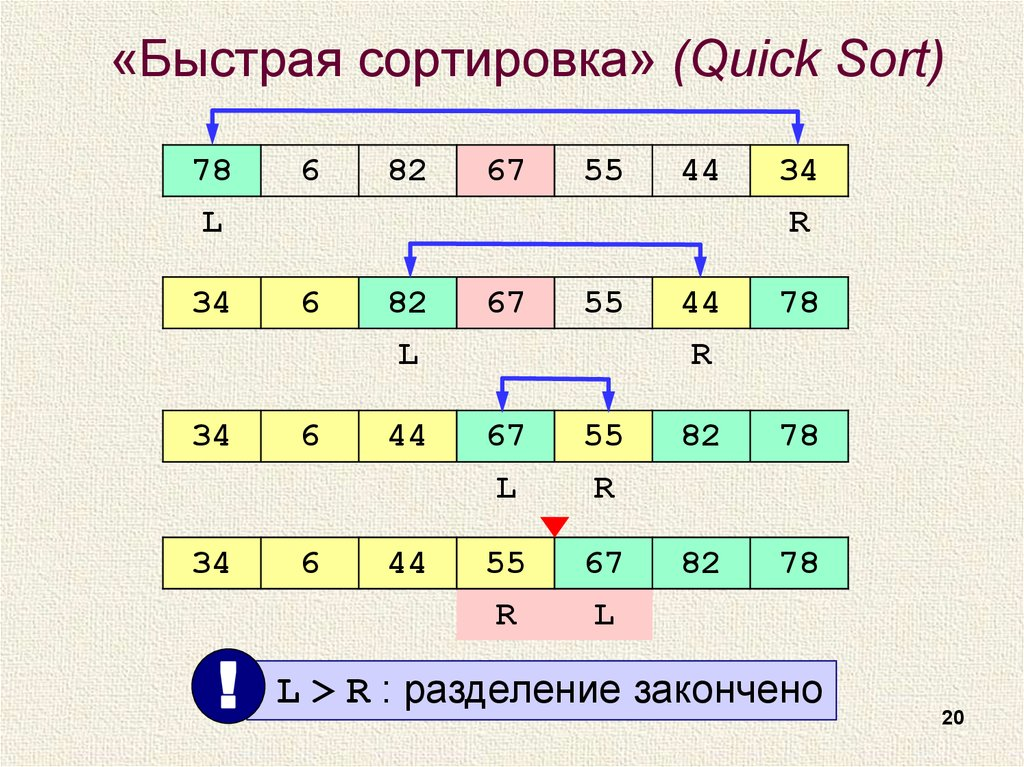
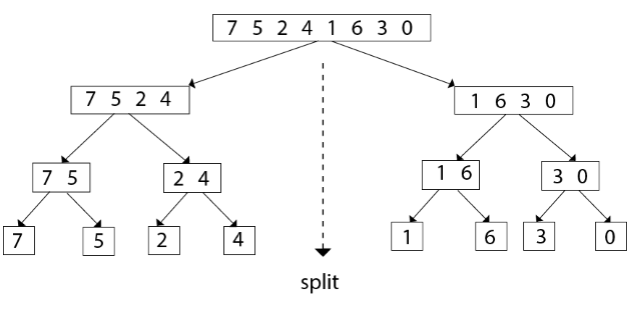
Quicksort и Merge Sort: эффективная сортировка больших массивов

Quicksort разделяет массив на подмассивы с помощью опорного элемента.

Алгоритм имеет среднюю сложность O(n log n). Время выполнения алгоритма растёт быстрее, чем линейно, но медленнее, чем квадратично:

1. Сначала выбирается элемент массива: средний, случайный, первый или последний;
2. Все элементы меньше опорного перемещаются влево от него, а больше — вправо;
3. И всё то же самое повторяется с подмассивами.

Quicksort подходит для работы в оперативной памяти, но нужно правильно определять опорный элемент. Для этого используются случайный подбор опорного элемента или метод медианы из трёх значений (сумма трёх значений за вычетом минимального и максимального).

Медиана — значение, которое будет совпадать с серединой данных, а если нужно определить ее из чётных чисел, то считается среднее из двух.

Merge Sort имеет среднюю сложность O(n log n) во всех случаях.

Он объединяет отсортированные подмассивы в один полностью отсортированный массив:

1. Массив делится пополам каждый раз, пока не останутся отдельные элементы;
2. И в конце концов подмассивы «собираются» снова, но уже в отсортированном виде.

Merge Sort весит больше, чем Quicksort. Зато он более стабилен и подойдёт для обработки больших файлов или для поток данных.

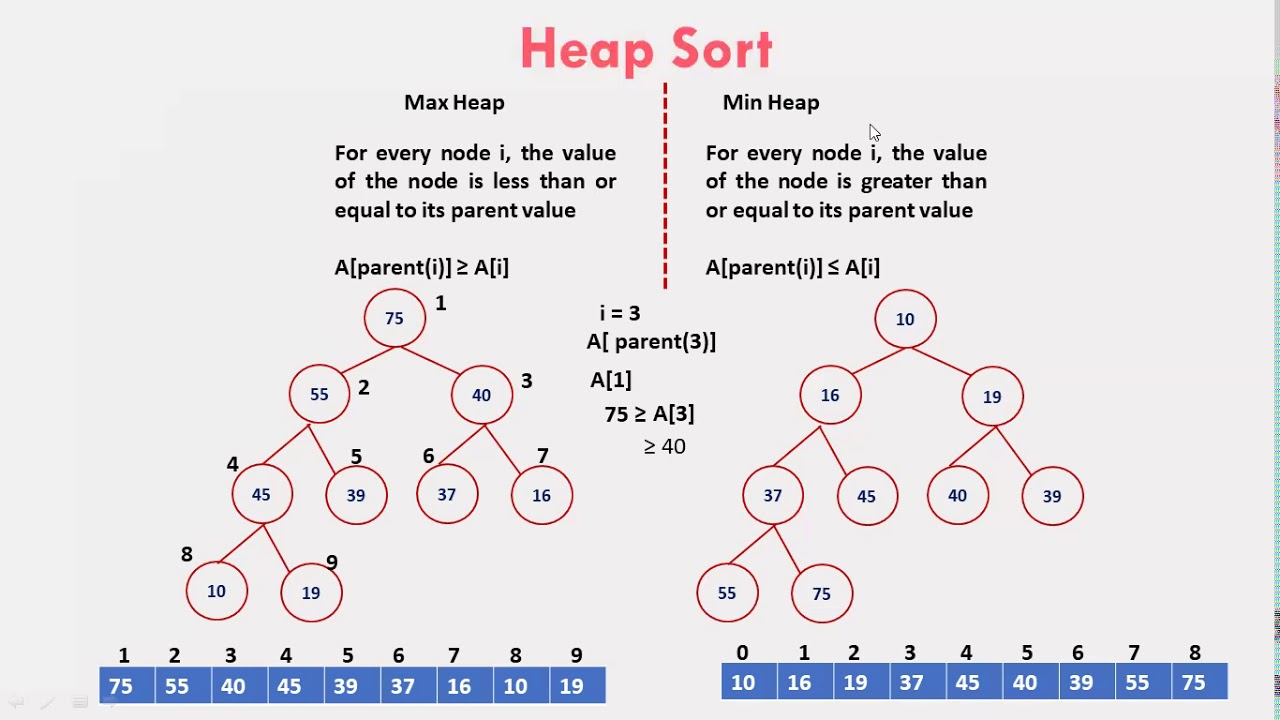
Heap Sort: сортировка для работы с приоритетами

Heap Sort — алгоритм сортировки двоичной кучи (структуры данных), где каждый раз минимальное значение находится и помещается в начало списка. Процедура повторяется каждый раз, пока структура не будет полностью отсортирована.

Хорош этот алгоритм тем, что подойдёт для сортировки данных по приоритету для создания частичных выборок:

1. Сначала массив преобразуется в двоичную кучу;
2. Затем для max-heap выделяется максимальный элемент и заменяется следующим, более «низким»;
3. Далее создаётся правильный порядок с помощью функции maxHeapify() или heapify();
4. Процесс повторяется до тех пор, пока не будет сформирован правильный порядок для всех элементов.

Heap Sort имеет сложность O(n log n) — она растёт быстрее, чем линейно, но медленнее, чем квадратично. Для метода не нужна дополнительная память для хранения промежуточных результатов.

Работа с графами

Мы когда-то упоминали в этой статье, графы используются для аналитики данных в backend-разработке. С помощью них определяется связь элементов друг с другом. Графы состоят из вершин, рёбер и весов, связей между рёбрами и вершинами.

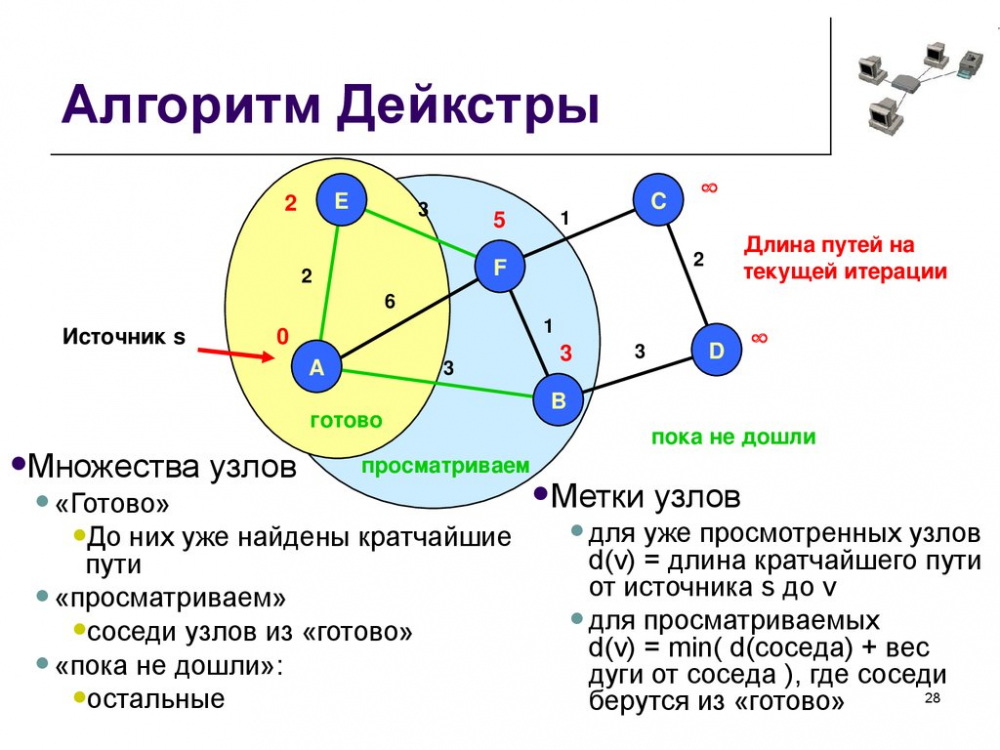
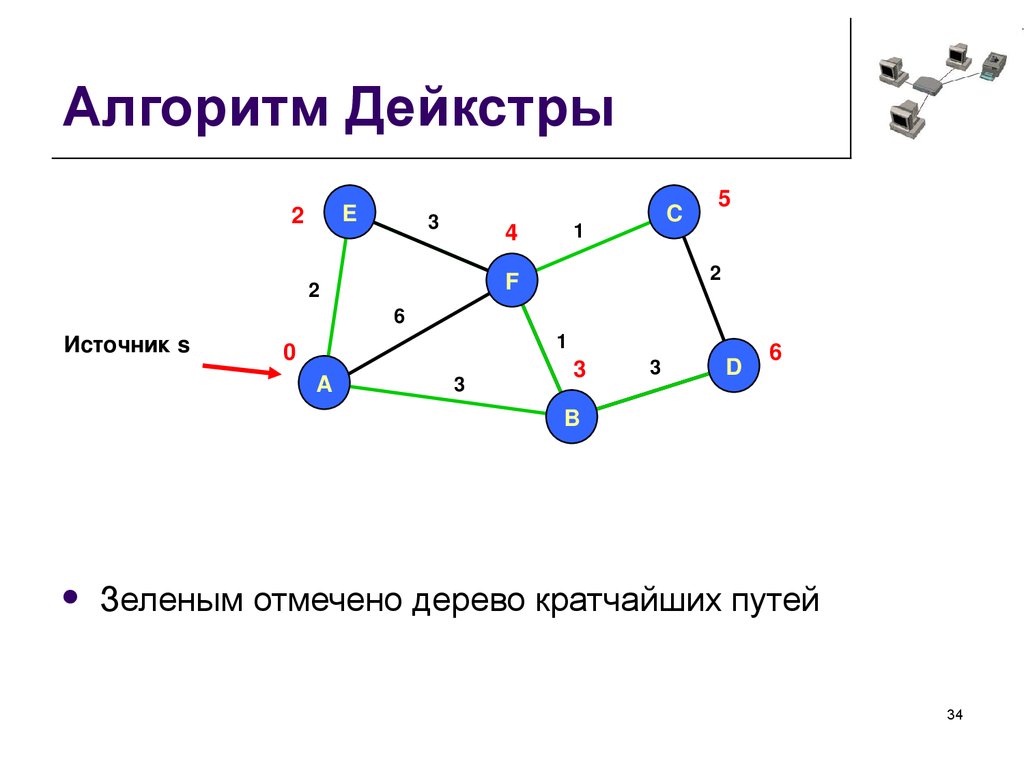
Алгоритм Дейкстры: нахождение кратчайшего пути

Алгоритм Дейкстры используется для нахождения самого короткого пути от одной вершины ко всем остальным. Этот алгоритм работает в системах навигации и приложениях, где нужно подобрать самый оптимальный маршрут между двумя элементами. А ещё алгоритм Дейкстры используется, например, для определения поведения NPS в играх или чтобы понять, как будет двигаться робот в определённой местности.

1. Сначала определяется главная вершина. Расстояние до неё, при этом, равно нулю, а до всех остальных вершин задаётся вручную (ну или определяется автоматически).
2. И далее алгоритм идёт от соседней (относительно начальной) вершины до следующей. И так, пока цель не будет достигнута.

Алгоритм Дейкстры имеет сложность O(V²), то есть, растёт квадратично. Сложность может уменьшиться до O(E log V) при работе с очередями приоритетности.

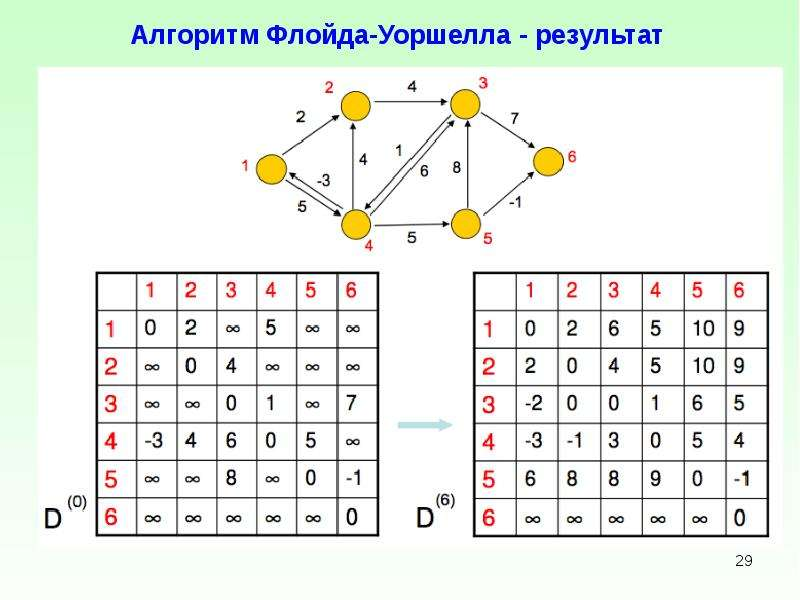
Алгоритм Флойда-Уоршелла: нахождение всех кратчайших путей

Если смысл Дейкстры в том, чтобы искать наиболее короткий путь от начальной вершины к остальным, то смысл алгоритма Флойда-Уоршелла в том, чтобы находить самый короткий путь между всеми вершинами.

1. Сначала создаётся матрица расстояний, где каждая ячейка [i][j] содержит вес ребра (i,j) или бесконечность, если ребра нет;
2. Для каждого узла проверяется возможности оптимизации пути между двумя другими узлами;
3. Далее матрица расстояний обновляется и ранжируется по самым коротким путям.

Алгоритм Флойда-Уоршелла имеет сложность O(V³), то есть, растёт кубически, и подходит для анализа связей между вершинами.

Алгоритмы хеширования

Хеш-функция — алгоритм, который принимает обычный текст и преобразовывает его в хешированный размером в 128 бит. Хеширование используется в backend разработке, например, при создании ключей шифрования исходя из пароля.

К плюсам хеширования можно отнести то, что один текст имеет строго один хешированный «вариант», а оригинальный текст не получится восстановить только с помощью хеша.

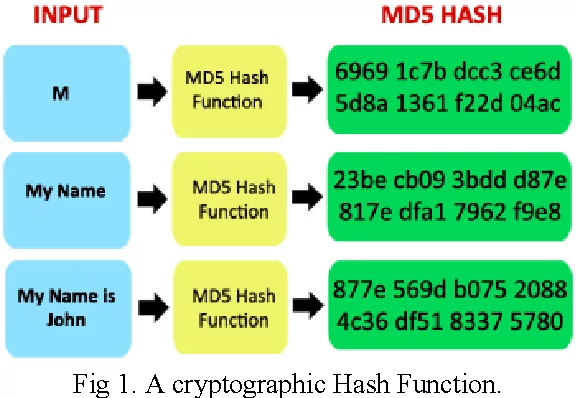
MD5 (алгоритм дайджеста сообщений 5) — самая популярная хеш-функция. Она используется для проверки целостности данных.

Раньше считалось, что два разных фрагмента не могут дать один и тот же MD5 хеш. Но система была взломана: в 2005 году китайские криптологи опубликовали статью с описанием алгоритма, который помогает найти 2 разные последовательности, но с одним MD5 хешем.

SHA — сразу несколько версий алгоритма (SHA-1, SHA-256, SHA-512). Сейчас распространены SHA-256 и SHA-512 с выходом дайджеста сообщений в 256 и 512 бит соответственно.

SHA используется для создания цифровых подписей и сертификатов безопасности — всё благодаря устойчивости алгоритма к «коллизиям» (иными словами, взломам) и постоянным обновлениям.

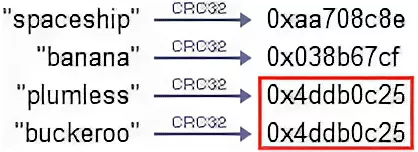
CRC32 (циклический избыточный код) — ещё одна хеш-функция для проверки целостности данных. CRC нельзя использовать для защиты данных от атак, поскольку ее основная задача — быстро обнаружить изменения данных при передаче или хранении.

CRC32 подходит для работы с сетевыми протоколами и для базового обеспечения целостности данных.

Работа с деревьями

Работа с деревьями — основа backend разработки. С помощью нее можно эффективно и правильно организовывать и хранить данные.

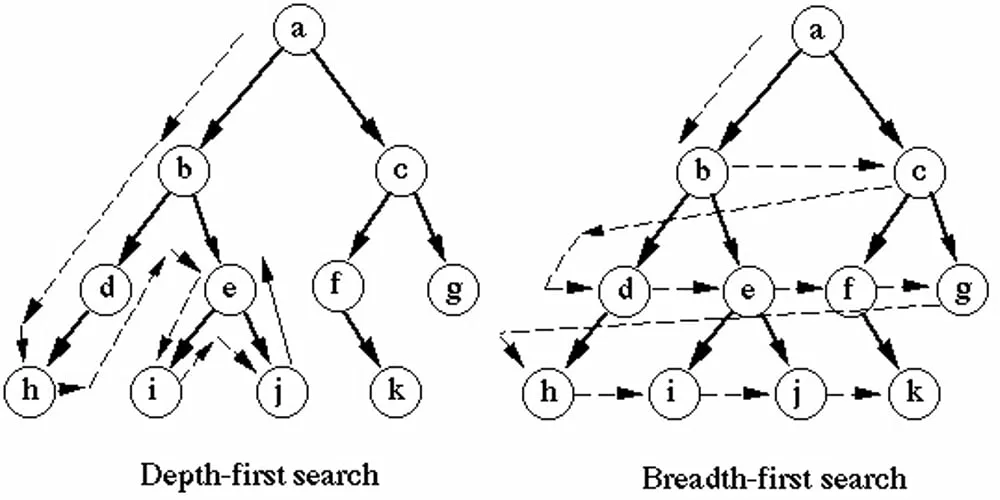
Алгоритм обхода деревьев (DFS, BFS)

Обход деревьев, если коротко, нужен для того, чтобы обработать каждый узел в своём порядке. Есть 2 главных способа обхода: поиск в глубину (Depth-First Search, DFS) и поиск в ширину (Breadth-First Search, BFS).

Принцип поиска в глубину (DFS) — сначала анализируются все «вторичные» (ну или дочерние) узлы одного поддерева, а потом следующее поддерево. DFS полезен для того, чтобы сначала проанализировать все узлы, а потом уже искать элементы с определённым условием.

Принцип поиска в ширину (BFS) — здесь анализируются все узлы на текущем уровне дерева, а уже потом осуществляется переход к следующему уровню. BFS подходит для нахождения кратчайшего маршрута в неглубоких структурах.

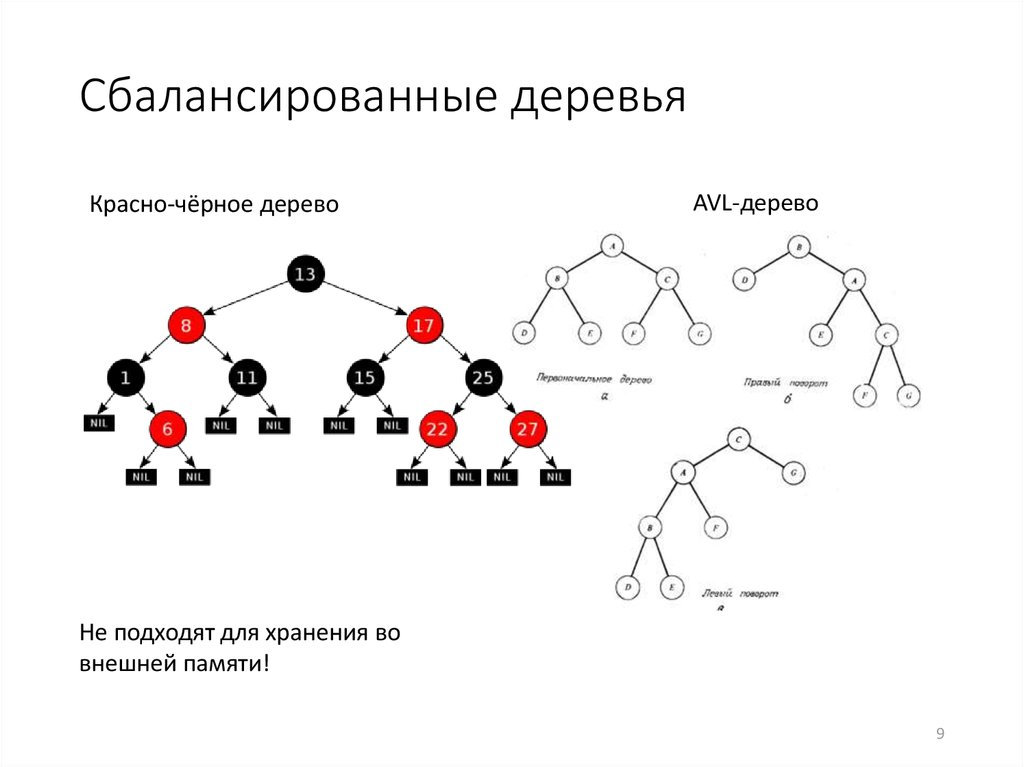
Балансировка деревьев (AVL, красно-чёрное дерево)

Без балансировки вставка и поиск могут занимать ну очень много времени из-за огромной глубины дерева данных.

AVL-деревья — двоичное дерево поиска с быстрым доступом к данным. При каждом добавлении или удалении элемента дерево автоматически балансируется. А это означает, что сложность операций всегда будет равна O(log n).

Красно-чёрные деревья менее сбалансированы по сравнению с AVL, зато операции вставки и удаления проводятся быстрее (за счёт меньшего количества вращений дерева).

Глобально: разница между двумя этими подходами в том, что: путь от корня (основания) дерева AVL — не более ~1,44 lg(n+2), а путь от корная красно-чёрного дерева — не более ~2 lg(n+1). AVL-деревья быстрее ищут данные, но требуют больше времени на вставку и удаление. А красно-чёрные деревья более простые и стабильные в реализации из-за меньших требований к балансировке.

Алгоритмы сжатия данных

Алгоритмы сжатия данных нужны для обработки и передачи больших объёмов информации в backend разработке. А потому и нужна оптимизация.

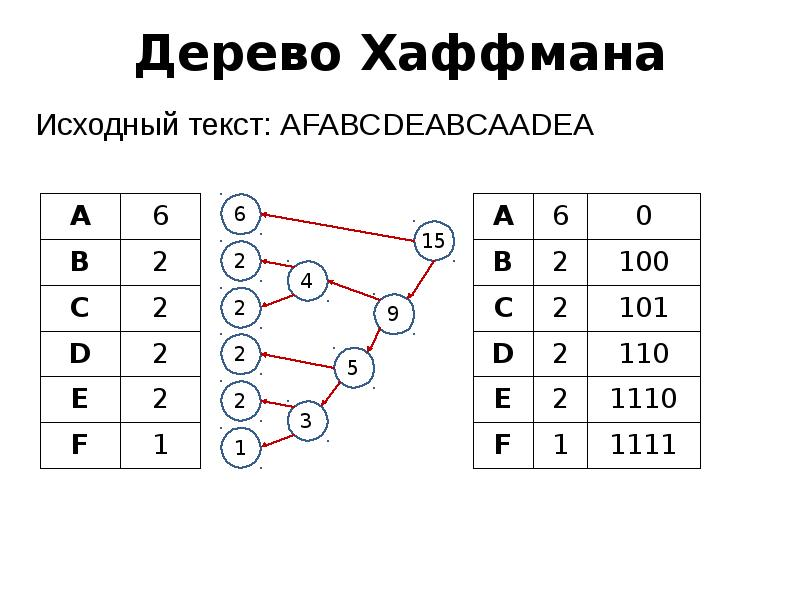
Huffman Coding: оптимизация хранения и передачи данных

Алгоритм Хаффмана (Huffman Coding) — один из видов алгоритмов префиксного кодирования. С помощью него можно уменьшить размер данных, при этом, «выигрывая» как в скорости, так и в объёме.

Символы, которые появляются чаще всего, кодируются более короткими последовательностями, а символы, встречающиеся реже, имеют более длинную последовательность.

Код Хаффмана — основа форматов сжатия по типу JPEG и MP3.

LZ77/LZ78: алгоритмы для компрессии больших объёмов данных

Алгоритмы семейства Lempel-Ziv — база современных методов сжатия без потерь качества и производительности. С помощью них большие по объёму данные сжимаются за счёт поиска повторяющихся последовательностей внутри массива.

Принцип работы LZ77 — второе и последующее совпадение данных ссылается на самое первое совпадение.

Принцип работы LZ78 — создание динамического словаря «фраз» по мере обработки данных. В процессе добавляются новые комбинации символов («фразы») по мере их обнаружения.

На этих алгоритмах строится форматы архивирования файлов по типу ZIP и GZIP.

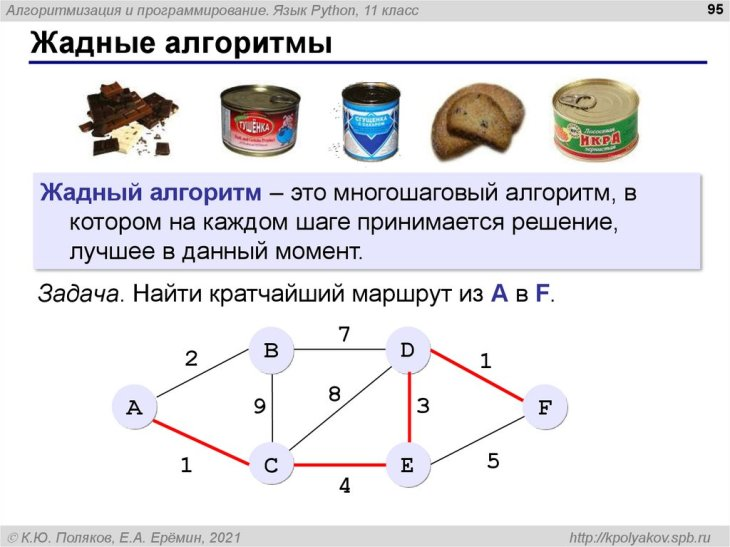
Жадные алгоритмы

Жадные алгоритмы — класс алгоритмов, внутри которых данные принимаются локально. «Жадными» они названы потому, что требуется найти самый оптимальный способ решения с минимальными затратами в backend-разработке.

Алгоритмы «наиболее подходящего выбора»: оптимизация решений

Фишка жадных алгоритмов в том, что каждый шаг локально выбирается лучшим. При этом финальный результат не может быть самым оптимальным. Поэтому важно внимательно анализировать условия задачи.

Задача о рюкзаке — здесь вам нужно выбрать максимальное количество предметов (рёбер) по большей стоимости (ценности) без превышения вместимости (веса) рюкзака (контейнера). В жадном подходе все предметы сортируются по стоимости за единицу веса и добавляются в рюкзак в порядке убывания.

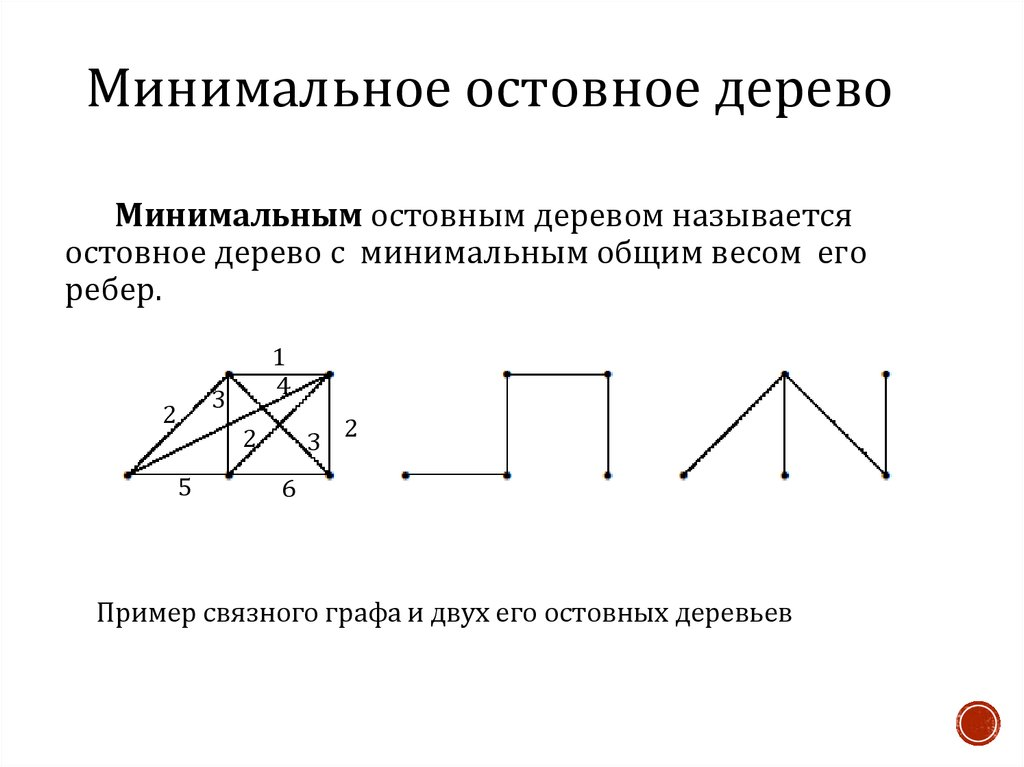
Минимальное остовное дерево через алгоритм Прима. Здесь поэтапно выбирается ребро с минимальным весом, которое соединяет уже включенные вершины с остальными.

Алгоритм Дейкстры мы уже разбирали выше. Если коротко: он используется для поиска кратчайшего пути от одной вершины графа до всех остальных. Основывается на выборе наименьшей стоимости пути из всех доступных на каждом шаге.

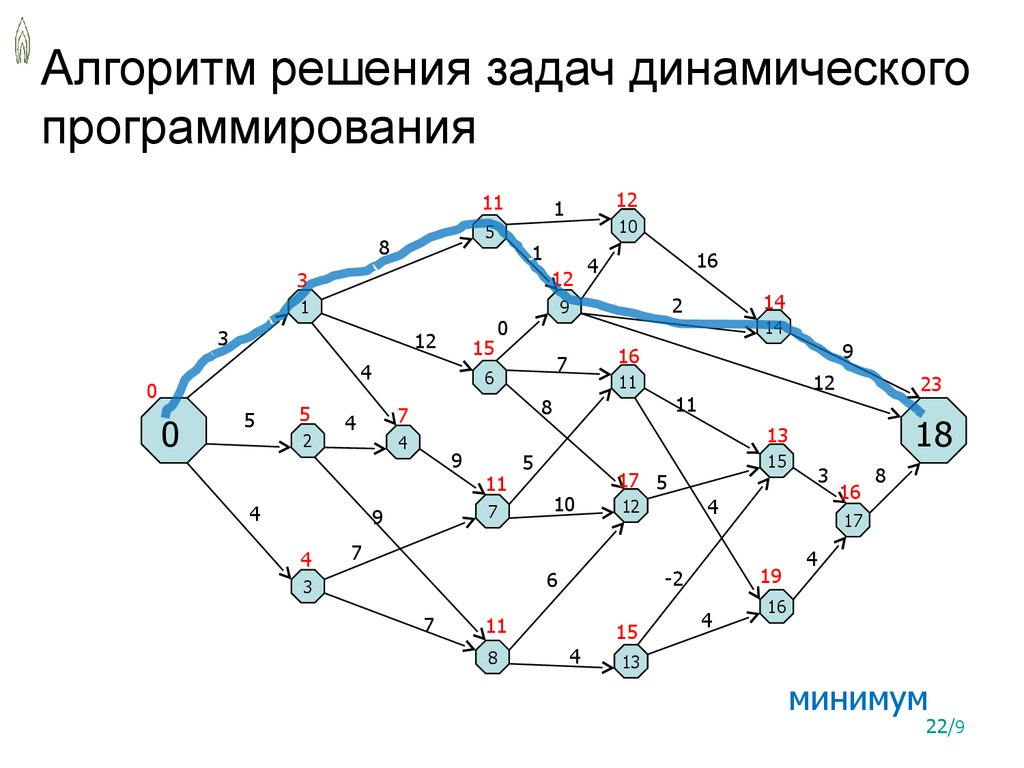
Динамическое программирование

С помощью динамического программирования решаются задачи оптимизации в backend-разработке. Происходит разбивка одной большой задачи на более простые. При этом, используется информация об уже проведённых вычислениях, чтобы не было повторов.

Алгоритм поиска подстроки (Longest Common Subsequence): анализ строк

Грубо говоря, этот алгоритм помогает найти определённый повторяющийся сценарий в тексте. Если строка содержит этот паттерн, то вы получаете ответ «да» или прямую ссылку, где этот паттерн впервые был представлен. Это в целом основной принцип криптографии, архивирования и компиляции.

Алгоритм имеет сложность O(n*m), где n и m — длины сравниваемых между собой строк. При этом, таблица с выводами заполняется последовательно, по мере нахождения паттернов.

Алгоритмы для работы с потоками данных

Для обработки данных в backend в режиме реального времени используются специальные алгоритмы: Sliding Window и Bloom Filter — с максимальной итоговой производительностью.

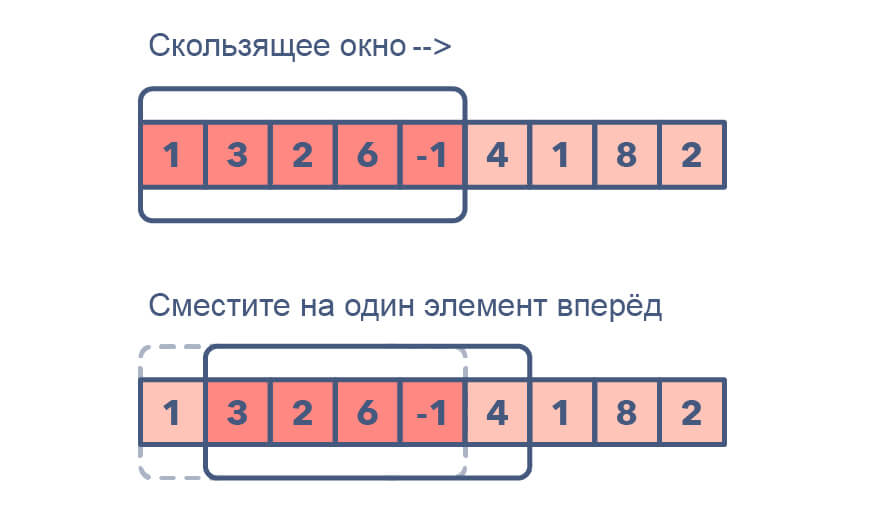
Sliding Window: обработка данных в реальном времени

Алгоритм скользящего окна используется для обработки непрерывного потока данных. Данные здесь разбиваются на небольшие окна определённой длины. Даже при самых высоких нагрузках и минимальном времени, весь поток хранить не нужно — и всё это благодаря скользящему окну.

Со скользящим окном можно работать при мониторинге трафика или отслеживании активности пользователей. При этом, всю историю наблюдений загружать не нужно — анализируются данные только конкретного окна.

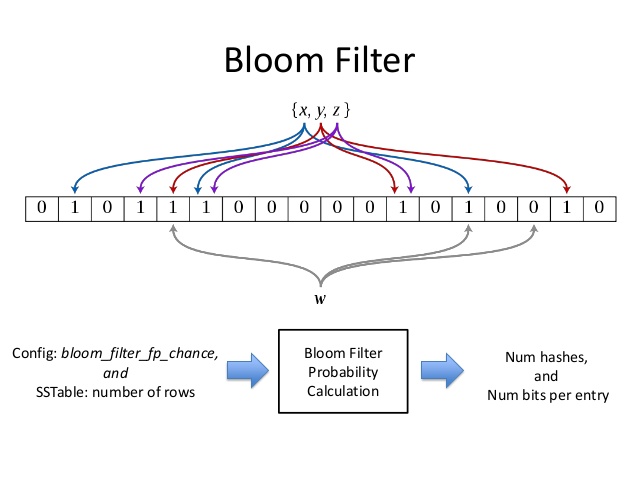
Bloom Filter: проверка существования элемента в наборе

Фильтр Блума — структура данных, которая используется для того, чтобы проверить, принадлежит ли конкретный элемент конкретному массиву данных.

Фильтр Блума занимает гораздо меньше места в сравнении с обычными структурами данных. С помощью него можно быстро проверить существование элемента через использование нескольких хеш-функций. По такому же принципу работает спам-фильтр в почтовом клиенте.

Все перечисленные и описанные выше алгоритмы критически важны для реализации практически любых задач backend’а. Как правило, их не нужно реализовывать с нуля, но нужно понимать принцип работы каждого. Потому что именно от сложности зависит время, которое тратится на решение конкретной задачи.