Передать данные и остаться в безопасности: алгоритмы шифрования в IT

IT-блогер Alek OS сделал подробное видео о развитии криптографии в эпоху компьютеров. Какие алгоритмы возникали, как они устаревали, как решалась проблема передачи ключа злоумышленникам и последующей дешифровки.

Вот, о чём рассказывают в видео:

1. Люди шифровали сообщения с II века до н.э. и все шифры были взломаны до середины XX века.
2. Криптоанализ помог расшифровать древние манускрипты и иероглифы, внося вклад в историческую науку.
   
3. Последняя попытка создать невзламываемый шифр вручную использовала ключ шифрования равный размеру сообщения.
   
4.  Изобретение компьютера стало технологическим прорывом, позволившим оперировать двоичными числами и изменить подходы к шифрованию.
   
5. Компьютеры используют двоичную систему счисления и стандарт кодирования символов, например, ASCII для шифрования информации.
   
6. Способы шифрования информации не изменились за тысячи лет и сводятся к замене и перестановке, но теперь на уровне битов.
   
7. Битовая операция XOR используется в шифровании, позволяя применять к двоичным числам математические операции.
   
8. Алгоритм шифрования Люцифер, разработанный IBM, стал основой для создания блочного шифрования и использовал сеть Фейстеля.
   
9. DES (Data Encryption Standard) был принят в 1977 году как мировой стандарт шифрования данных, но позже был признан уязвимым из-за короткой длины ключа.
   
10. Асимметричное шифрование и цифровая подпись стали возможны благодаря алгоритмам с открытым ключом, таким как RSA.
    
11. Алгоритмы шифрования продолжают развиваться, но история показывает, что любой шифр может быть взломан со временем.

Ниже — транскрибация ролика на русском языке.

На протяжении всей истории люди шифровали и расшифровывали свои сообщения вручную, начиная со II века до н.э. во времена правления Юлия Цезаря, заканчивая шифром Виженера, который плавно перерос в механические устройства, одно из которых нам известно под названием Энигма.

Объединяет все эти шифры только одно — все они, без исключения, были взломаны. Вплоть до середины XX века криптоаналитикам удавалось брать верх над любым (в кавычках) невзламываемым шифром, который кропотливо изобретался десятилетиями лучшими криптографами в надежде обеспечить безопасность передачи сообщений. При этом нельзя сказать, что криптоанализ это абсолютное зло, которое не давало человеку безопасно коммуницировать.

Благодаря ему, за многие века была собрана колоссальная база методик по взлому ручных шифров, что в конечном итоге позволило расшифровать многие древние манускрипты, египетские иероглифы и множество подобных древних артефактов, которые дали нам новые представления о событиях и жизни людей в те времена, от которых остались лишь слухи, легенды и чудеса света, которые люди не способны объяснить до сих пор.

Последняя ручная попытка создать то, что никогда не будет взломано, заключалась в использовании ключа шифрования равным размеру исходного сообщения. Да, это действительно решало проблему со взломом. На поиск правильного ключа методом полного перебора могли уйти миллионы лет. Однако и на само шифрование и расшифрование подобного сообщения уходило столько времени, что делало этот шифр абсолютно бесполезным. Особенно учитывая то, что создавались они в первую очередь для военных целей, где каждая секунда играла роль.

Мы подошли к неутешительному выводу. Человек окончательно уперся в пик своих криптографических возможностей. Это не было бы так критично, если бы не тот факт, что это было именно то время, когда половина мира была по уши погружена в войну, а информация беспрепятственно и безостановочно передавалась в виде радиоволн, давая без всяких проблем себя перехватывать.

Человеку срочно требовалась помощь. Нужен был какой-то технологический прорыв, некий рывок, который бы на века мог обеспечить былую защиту информации от любых методов взлома. Таким рывком стало изобретение компьютера. Тогда ещё никто не догадывался, к чему приведёт это вычислительное устройство. Но именно оно изменило всё.

Изобретение компьютера и новые наборы шифров

Главное отличие работы компьютера от работы человека в том, что если человек в основном оперирует текстовыми символами, то компьютер оперирует только числами. Причем не абы какими, а только двоичными. Это означает, что теперь абсолютно любую информацию, которую нам предстоит зашифровать, мы сначала должны будем перевести в единицы и нули — двоичную систему счисления.

Для того, чтобы это стало возможным, каждому текстовому символу были придуманы числовые обозначения, которые затем организовывались в таблице и получили название «стандарт кодирования символов». Например, согласно стандарту ASCII, символ A хранится в компьютере как число 65, но только в двоичном виде. Символ B как число 66 и так далее, и так далее.

Поэтому совершенно неудивительно, что такой маленький для нашего восприятия текст в компьютере представляется таким вот большим для нашего восприятия числом. Именно эти биты двоичного числа и будут шифроваться, благодаря чему на выходе мы получим какое-то другое зашифрованное число. Хоть сама информация и претерпела преобразование в двоичный вид, сами способы шифрования за последние тысячи лет абсолютно никак не менялись.

Замена, перестановка и их комбинации это по-прежнему единственные способы что-либо зашифровать.

XOR как метод шифрования

Однако, если раньше минимальной единицей перестановки была буква, то сейчас это минимальной единицей стал бит. Это означает, что теперь мы можем осуществлять перестановки как внутри каждой отдельной буквы, так и переставлять отдельные биты двух отдельных букв. Примерно то же самое касается и способа замены. Помимо замены целых символов, мы можем спокойно менять отдельно взятые биты. Однако изменение это теперь стало довольно примитивным.

Единицу мы можем заменить только на ноль, а ноль только на единицу. Всё это нам очень сильно напоминает битовую операцию XOR, в которой одинаковые биты двух чисел дадут ноль, а разные биты дадут единицу.

Очевидно, что одной операцией XOR мы можем не ограничиваться. Двоичные числа позволяют нам применять к ним любые математические битовые операции, вроде сдвигов, которые будут приводить к полному изменению исходной информации, что открывает учёным новый необъятный мир криптографии, в котором они с усиленным энтузиазмом начнут изобретать новые невзламываемые шифры.

Почему разные шифры — это плохо?

Что происходит, когда каждый начинает создавать то, что он хочет? Создается хаос, в котором нет места упорядоченности. Так произошло и в случае с шифрами. Алгоритмы, которые появлялись примерно в одно и то же время в разных частях планеты, никак не были согласованы друг с другом, а следовательно, никакой стандартизацией не пахло. Банальная несовместимость программного обеспечения на разных компьютерах в связи с использованием разных алгоритмов шифрования просто не позволяла двум разным людям общаться между собой.

Плюс это было как минимум небезопасно. Никто не знал, что находится внутри этих алгоритмов. Никто не знал, как хранятся и используются ключи. Отсутствие доверия к подобным разработкам привело лишь к одному. Было решено создать алгоритм, который стал бы единым стандартом шифрования для всего мира.

Люцифер (DES)

Был проведен конкурс при поддержке правительства США, в результате которого американская компания IBM представила свой алгоритм шифрования по символичным названиям Люцифер. Последняя версия этого алгоритма, которая была принята, основывалась на так называемой сети Фейстеля.

Названная эта сеть была в честь ученого Хорста Фейстеля, который являлся одним из разработчиков этого шифра. В частности, благодаря его идеям у нас появилось такое понятие, как блочное шифрование. Смысл в следующем. Вместо того, чтобы шифровать каждый символ последовательно друг за другом, как это происходило многие века, мы можем шифровать данные сразу целыми блоками.

То есть мы берем исходное двоичное число, разбиваем его на блоки, к примеру, по 64 бита, и каждый такой блок пропускаем через алгоритм шифрования. При этом, если исходный текст, или наоборот, остаток этого текста оказывается меньше 64 бит, то такой блок просто дополняется нулями до нужного количества.

Далее каждый такой блок разбивается на две части и пропускается через сеть Фестиля, которая состоит из 16 циклически повторяющихся раундов. На каждом раунде исходные данные меняют свой внешний вид, и на каждом раунде свой внешний вид меняет и ключ.

В итоге Люцифер получился настолько хорош, что появились реальные опасения, что его на самом деле никому не удастся взломать. Его ключ составлял 128 бит. Это означало, что на тот момент вычислительных мощностей, которыми обладали тогдашние компьютеры, попросту могло не хватить для перебора всевозможных ключей за какое-то приемлемое время. А учитывая, что блочные шифры были новинкой того времени, то каких-то больших исследований и статистик по взлому подобных алгоритмов не существовало, что снова осложняло их взлом.

Казалось бы, это и требовалось, а значит задача разработчиков Люцифера полностью выполнена. Однако у агентства национальной безопасности США на этот счет было немного другое мнение. Они предпочли на всякий случай оставить хотя бы небольшую уязвимость для взлома, чтобы в экстренном случае иметь возможность получить доступ к расшифровке. Поэтому их требованиями было следующее:

• Уменьшить ключ шифрования со 128 до 56 бит;
• Заменить предложенные s-блоки (которые мы вскоре увидим) на свои.
  

Сокращение ключа больше, чем в два раза, моментально сократило количество возможных ключей, а следовательно и время для полного их перебора.

Логика была следующая. У обычных людей и компаний нет такого мощного железа, которое позволило бы им перебрать такое количество ключей за приемлемое время. А значит, алгоритм для обычных пользователей полностью безопасен. Зато у АНБ доступ к таким мощностям есть, что и позволит им единственным в случае необходимости в любой момент получить доступ к информации.

Именно такая урезанная версия шифра Люцифер и была принята в 1977 году в качестве мирового стандарта шифрования данных, известный сейчас под названием DES.

Именно этот алгоритм мы с вами прямо сейчас реализуем с полного нуля на примере шифрования такого слова, как eternity. Все шифрование, как уже было сказано, осуществляется на уровне битов, поэтому все текстовые символы этого слова с помощью стандарта ASCII примут следующий вид:

			01100101 01110100 01100101 01110010 01101110 01101001 01110100 01111001
		

Далее по сценарию алгоритма все это исходное число должно было разбиться на блоки по 64 бита, но так как наша фраза уже является 64-битным числом, оставляем ее как есть.

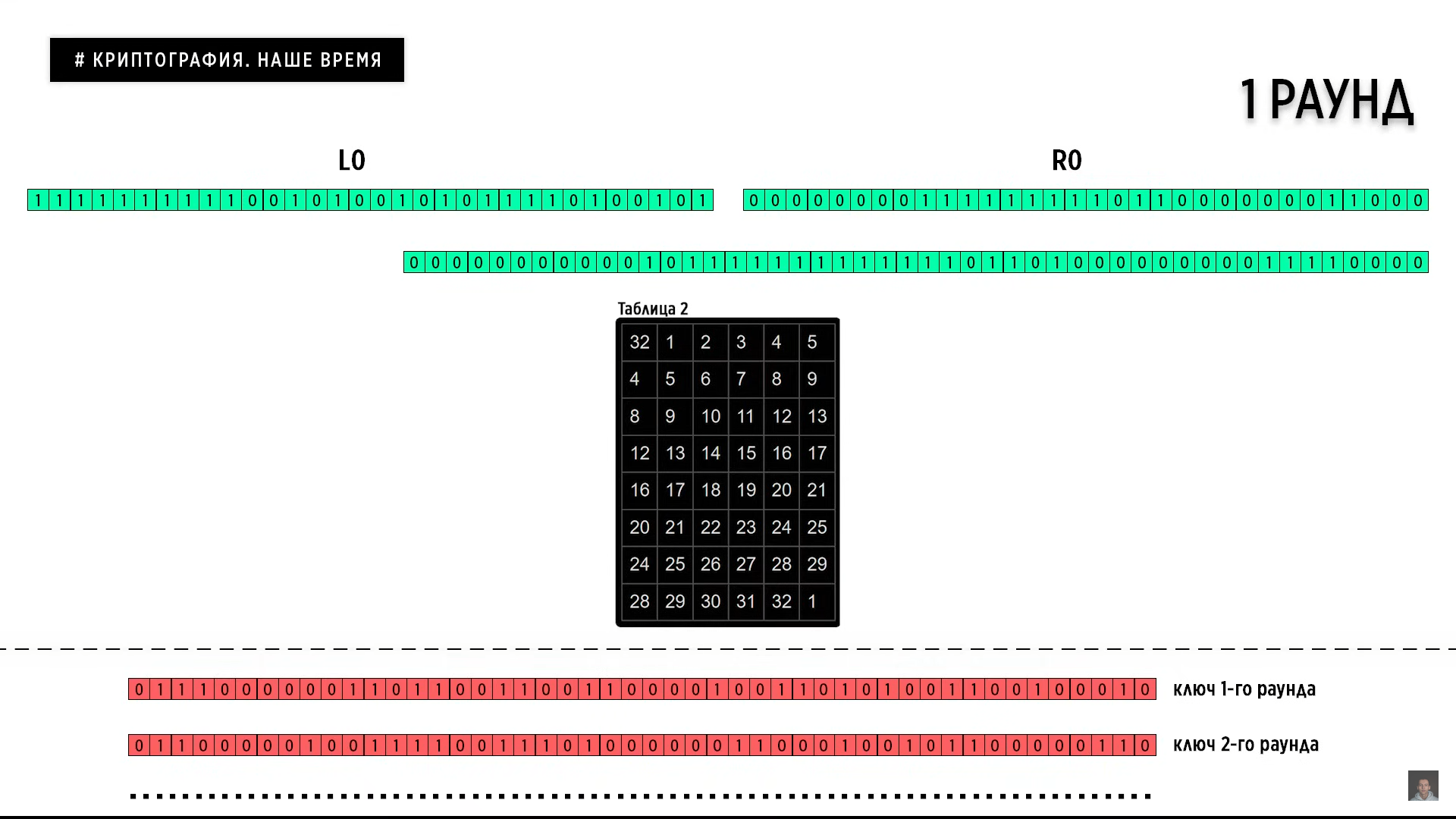
Перед тем, как мы приступим к выполнению 16 раундов Фестиля, нам нужно произвести первоначальную перестановку всех битов исходного сообщения. Это и все остальные перестановки, как мы вскоре увидим, осуществляются на основе уже подготовленных заранее таблиц, которые легко можно будет различить по их соответствующему номеру.

В этой таблице указаны номера битов нашего исходного числа в том порядке, в котором они должны теперь стоять. Поэтому просто меняем их местами, получаем такое вот число и делим его на две части по 32 бита, получив тем самым числа L0 и R0. Именно эти два числа после прохождения всех 16 раундов и будут хранить в себе итоговый шифр. Однако для того, чтобы их выполнить, нам потребуется сформировать 16 специальных 48-битных ключей для каждого такого раунда. Формируются они из исходного ключа шифрования, который мы выберем.

В нашем случае это, конечно же, будет ключ AlekOS, который мы снова с помощью таблицы ASCII переведем в двоичный бит и дополним его нулями, для того, чтобы он тоже стал кратен 64 битом.

Для чего? Для того, чтобы снова переставить все эти биты, но уже по другой таблице. Данная перестановка, кроме перемешивания бит, отсекает каждый восьмой бит 64-битного ключа. Поэтому на выходе мы получим те самые 56 бит, которым и должен равняться ключ данного алгоритма. Отталкиваясь именно от этого ключа, мы должны получить 16 уникальных ключей для каждого раунда. Для этого мы разобьем ключ на две части по 28 бит. Для каждой такой части мы произведем циклический сдвиг влево согласно третьей таблице, после чего склеим ключ и с помощью четвертой таблицы перестановок сожмем его до 48 бит, получив тем самым ключ первого раунда. Чтобы получить ключ второго раунда, мы продолжаем сдвигать две части исходного ключа уже по второму столбцу, затем снова его склеиваем, сжимаем до 48 бит и переходим к созданию третьего ключа, продолжая делать все то же самое. До тех пор, пока не получим 16 готовых 48-битных ключей.

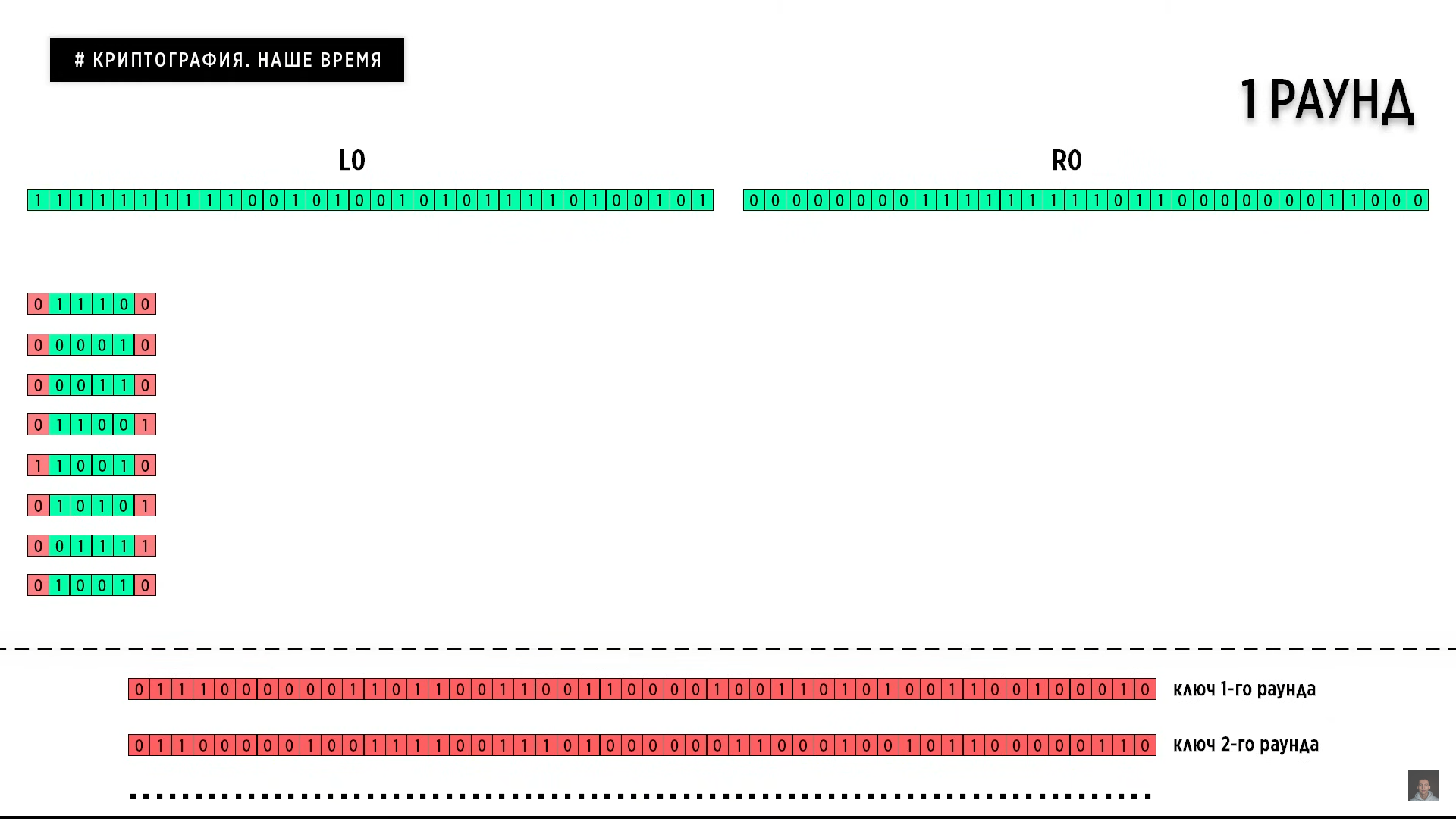
Окей. Переходим к цикличному выполнению 16 раундов, которые выглядят абсолютно одинаково. На первом раунде мы берем правую часть исходного сообщения R0 и расширяем ее согласно таблице перестановок с 32 до 48 бит. Расширение происходит за счет того, что мы каждым 4 битам приписываем 2 бита по бокам.

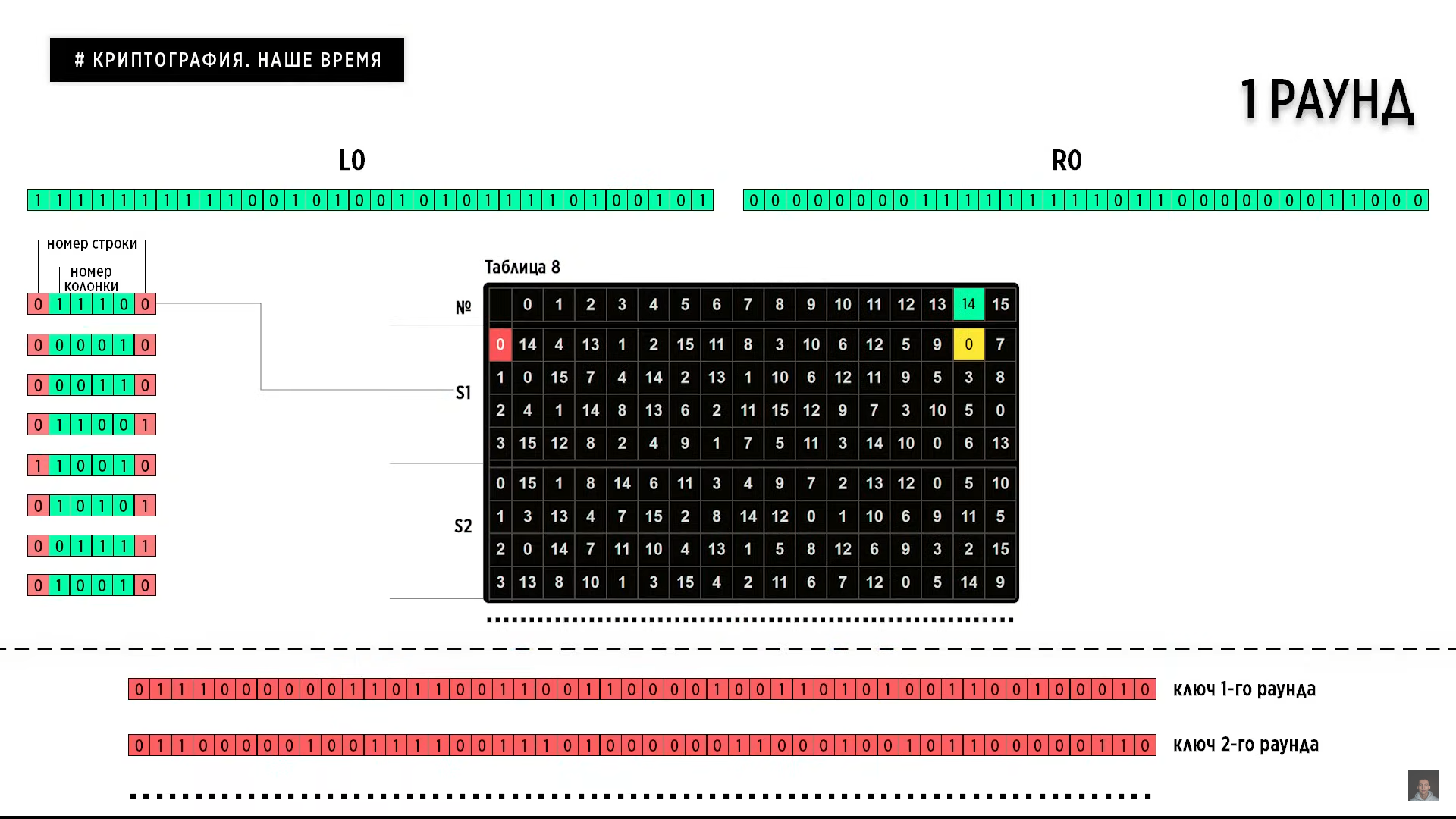
В итоге новое полученное значение R0 миксуем с ключом текущего раунда (в данном случае первого) и разбиваем итоговый результат на 8 групп по 6 бит. Каждое из этих значений мы разбиваем еще на две части. Это 4 центральных бита и 2 бита по бокам. 2 бита по бокам являются числом, представляющим собой номер строки.

4 бита являются числом, представляющим номер колонки. Все эти строки и колонки относятся к таблице тех самых s-блоков, замена которых было вторым требованием Агентства Национальной Безопасности. Так как в свое время они намеренно ослабили ключ, то было большое подозрение, что и замена s-блоков произведена точно с такой же целью, то есть ослабить шифр. Каково было удивление, когда спустя целых 20 лет будет доказано, что наоборот. Именно эти блоки очень устойчивы к дифференциальному и линейному криптоанализу, которые появились только в 90-х годах. Почти на 20 лет позже появление самого шифра DES. Это говорит лишь о том, что секретные службы уже владеют технологиями, которые человечество типа изобретет только спустя десятилетия.

Ну окей. Если до этого времени мы модифицировали исходные данные путем перестановок, то теперь мы применяем метод замены. На пересечении строки и колонки в каждом из S-блоков мы выписываем числа, которые после склейки дадут нам новое 32-битное число, биты которого мы в очередной раз переставим местами. В конце раунда полученное значение миксуем с левой частью исходного сообщения L0, и то, что получилось, будет являться значением R1, которое вместо R0 отправится во второй раунд. Очевидно, что вместо L0 во второй раунд отправится L1, которое теперь равняется тому, чему изначально равнялся R0. Второй раунд даст нам числа L2 и R2, третий раунд даст числа L3 и R3, а шестнадцатый раунд даст числа L16 и L16. Который мы, перед тем как склеить, должны будем поменять местами, после чего произвести завершающую обратную перестановку и получить итоговый шифр.

А теперь главное преимущество такого алгоритма: чтобы полученный результат расшифровать, нам даже не придется проделывать все эти шаги в обратном порядке. Нам нужно сделать абсолютно все то же самое для зашифрованного числа вообще никак не меняя сам алгоритм. Единственное отличие заключается в том что теперь на каждом в следующем раунде мы будем брать ключи не от 1 до 16, а от 16 до 1.

Электронная кодовая книга

Конкретно в нашем примере алгоритм шифрования завершится всего за одну такую итерацию цикла, так как у нас всего один 64-битный блок. Но если мы возьмем большой текст, то то, что мы разобрали, будет выполняться для каждого отдельного блока. Однако при такой реализации можно заметить, что все наши блоки вообще никак не связаны между собой. А следовательно они могут быть зашифрованы параллельно друг другу. Такой режим шифрования называется электронной кодовой книгой. Проблема его в том, что он позволяет установить четкое соответствие между исходным и зашифрованным сообщением, что автоматически порождает статистический криптоанализ.

Что это значит? Хорошо продемонстрирует следующий пингвин.

Наша задача зашифровать все пиксели цвета в этой картинке, минуя заголовки и служебную информацию, чтобы впоследствии мы смогли ее открыть. Нет проблем. Щелкаем пальцами, но что мы видим?

Пингвин, хоть и зашифрованный, по-прежнему остаётся пингвином. Мы тупо не смогли зашифровать картинку мировым стандартом шифрования.

Почему? Потому что если мы разобьём все пиксели в этой картинке на блоке по 64 бита, то увидим, что все рядом стоящие блоки одного цвета имеют абсолютно одинаковые значения. Но, соответственно, все эти блоки после процедуры шифрования примут другой одинаковый цвет с помощью одного и того же ключа.

CBC

Конечно, этот пример сильно утрирован для такой маленькой картинки, однако он наглядно показывает проблему режима электронной кодовой книги. Что с этим делать? Ну, например, воспользоваться одним из оставшихся режимов шифрования, в которых каждый блок сообщения шифруется в зависимости от других блоков. Мы не будем разбирать их все, а посмотрим только режим CBC для того, чтобы понять, о чем я говорю. В этом режиме каждый исходный блок перед процедурой шифрования XOR`ится с предыдущим зашифрованным блоком. При этом у самого первого блока нет зашифрованного предшественника, поэтому его исходный вид XOR`ится с каким-то заранее заготовленным числом.

В итоге, несмотря на то, что мы по-прежнему используем один и тот же ключ для каждого блока, одинаковые пиксели пингвина становятся на выходе разными из-за дополнительного XOR`а, который уже на старте меняет биты числа. Получается, что каждый зашифрованный блок завязан на каждом. Это создает впечатление, что при искажении некоторых бит какого-то одного блока, расшифровка всего сообщения становится невозможной.

Спешу вас обрадовать, это не так. Например, в ходе передачи данных испортился один бит у первого зашифрованного блока. Разумеется, пройдя через процедуру расшифровки, мы получим совершенно искаженную последовательность, в которой мы еще к тому же применим операцию XOR с тем самым заготовленным числом для первого блока. И получим полную белиберду. Однако, передав зашифрованную последовательность во второй блок, мы начнём его ксорить только после корректной расшифровки этого второго блока. Поэтому в итоговом расшифрованном сообщении второго блока побьётся только один единственный бит. А так как все зашифрованные биты второго блока дошли без изменений, то они абсолютно корректно передадутся в третий блок, и начиная с третьего блока, расшифровка пойдёт без всяких проблем.

Одноалфавитный шифр

Нескончаемый поток бит в сетях передачи данных стал для нас ежедневной нормой. Эта норма сопровождается четырьмя важными особенностями:

1. неизвестность размера потока;
2. высокая скорость передачи во избежание задержек;
   
3. низкое потребление памяти для простоты реализации;
   
4. отсутствие влияния искажения бит на всю остальную информацию.
   

Блочные алгоритмы соответствуют этому лишь частично. Поэтому учёные продолжили изобретение новых поточных алгоритмов, которые могли бы шифровать не целые блоки данных, а лишь небольшую группу бит, идущих друг за другом. Идея была максимально проста. Взять небольшую последовательность бит из этого потока и просто XOR`ить её с ключом. Затем взять следующую порцию бит и сделать то же самое. Всё это нам снова напоминает то, от чего мы пытались избавиться уже несколько веков.

Одноалфавитный шифр. Когда у нас есть один небольшой ключ, который мы дублируем над всеми символами сообщения и просто заменяем исходные буквы на символы ключа, стоящие над ними. Взломать такое в наше время не составляет никакого труда. Поэтому единственный вариант, при котором мы смогли бы оставить такой алгоритм, это если бы ключ полностью изменялся при каждом следующем шифровании битовой последовательности. Причем ключ этот должен быть полностью случайным без всяких зависимостей, чтобы его нельзя было предсказать и, соответственно, нельзя было так просто взломать.

Самое простое, что нам может прийти на ум, это заранее составить огромный список случайных ключей и хранить его в каком-то секретном месте. А так как какое бы ни было секретным место, оно гарантированно рано или поздно будет раскрыто, что автоматически сделает данный шифр максимально уязвимым. Потому что для того, чтобы его взломать, достаточно будет украсть этот источник с ключами. Раз эти ключи нельзя где-то хранить, значит они каким-то образом сами должны генерироваться в абсолютно случайной последовательности. Источников, которые человек в силу своей ограниченности считает случайными, в мире не так уж и много. Например, это может быть распад частиц, космическое излучение, тепловой шум или же просто постоянное подкидывание кубика.

Функция rand() и генераторы псевдослучайных чисел

Так или иначе, любой из этих физических способов либо очень дорогой, либо очень медленный. Плюс он не позволяет воспроизвести ранее полученное число, что делает невозможным проверки вычислений. Если представить, что цифровые данные должны передаваться со скоростью гигабайт в секунду, то в эту же секунду должны генерироваться сразу миллиард ключей. Разумеется, ни один из вышеперечисленных способов не способен обеспечить такую скорость. Поэтому вместо идеи абсолютной случайности, мы вынуждены сдаться и прийти к идее псевдослучайности, которая в свою очередь приводит нас к созданию генераторов псевдослучайных чисел.

Это всего лишь программный алгоритм, который при помощи математических формул выдаст нам на выходе последовательность чисел, которые будут почти независимы друг от друга. Слово «почти» является ключевым отличием псевдослучайного числа от просто случайного. Дело в том, что алгоритм сам по себе не может произвести ничего случайного. Он всегда будет выдавать числа по какому-то математическому закону. На это означает только одно — рано или поздно числа зациклятся. То есть начнёт воспроизводиться одна и та же последовательность. Поэтому если период последовательности будет достаточно мал, то и стойкость такого алгоритма будет крайне низкой.

Это стало понятно ещё в 40-х годах XX века, когда ученый Джон фон Нейман предложил использовать метод середины квадрата для получения десятичных псевдослучайных чисел.

К примеру, мы берем десятичное четырехзначное число, возводим его в квадрат, дополняем нулями, если количество его цифр нечетное, берем из его середины средние цифры и снова возводим это число в квадрат, получая тем самым рандомные числа, пока в один прекрасный момент все наше вычисление не станет зацикленным. Поэтому вместо этого способа был предложен линейный конгруэнтный метод, который послужил основой для всем известной функции rand(), которую все мы неоднократно использовали в языках программирования, когда хотели получить какое-то случайное число.

Весь этот алгоритм держится всего лишь на одной формуле. Мы берем значение x, которое по умолчанию чему-то равно, умножаем его на константу a, прибавляем к полученному результату константу c и получаем измененный x. Далее мы делим измененный x на некую константу m, получая остаток от деления. То, что получилось, и является псевдослучайным числом. Константа m — это не просто модуль, относительно которого вычисляется остаток. Это тот самый период, за который наша последовательность чисел выйти не может.

Почему? Потому что так работает математика. К примеру, у нас есть массив на три элемента, один индекс которых нам нужно получить. Если в ходе n-ной функции мы получим индекс, превышающий количество элементов массива минус один, то мы просто получим ошибку. Так вот, чтобы этого не произошло, нужно полученный индекс поделить с остатком на размер массива. В таком случае все индексы меньше длины массива в точно таком же виде будут возвращены в остатки. Но как только индекс превысит допустимый предел на единицу, то вместо ошибки мы просто перейдем в самое начало массива, взяв самое первое число. Превышение индекса на 2 даст нам второе число от начала, на 3 третье число, а на 4 мы снова перейдем на начало этого круга. Таким образом, благодаря делению с остатком мы всегда будем получать числа в диапазоне от нуля, до модуля минус 1. Что ж, хорошо, мы никогда не выйдем за пределы этого модуля, но все эти константы в разных языках программирования имеют разные значения, но все они подобраны так, чтобы числовая последовательность имела хорошие статистические свойства.

Например, в стандарте C99 для этого можно было увидеть, как число перед делением с остатком дополнительно делилось на 65536, что является аналогом сдвига вправо на 16 для того, чтобы отбросить 16 младших бит.

Хорошо. У нас есть рабочий алгоритм по генерации псевдослучайных чисел. В чем проблема? Проблема в том, что по полученным числам все эти константы вычисляются довольно легко. Поэтому данный генератор псевдослучайных чисел в криптографии неприменим. Нам нужен такой генератор, который бы вместо статичных констант использовал постоянно меняющиеся ключи в зависимости от заранее заданного ключа. Подобно тому, как это происходило в алгоритме DES.

RC4

Один из таких генераторов был реализован Рональдом Ревестом в 1987 году. В 1957 году в поточном алгоритме RC4. В течение 7 лет после своего появления этот алгоритм являлся коммерческой тайной, пока в один прекрасный день в 1994 году кто-то анонимно не опубликовал его в открытом доступе. Тем не менее это не помешало ему уверенно занять свою нишу, став одним из самых популярных поточных шифров того времени.Найдя свое применение в таких Wi-Fi протоколах, как Web, WPA или протоколах SSL и TLS.

Работает он следующим образом. На вход подается ключ в виде массива байт переменной длины от 40 до 2048 бит. Далее создается массив из 256 значений, который является всеми возможными перестановками одного байта от 0 до 255. Именно один из этих байтов будет каждый раз выбираться в качестве ключа для шифрования каждого последующего байта исходных данных. Для того, чтобы мы могли его выбрать непредсказуемым способом, используется тот самый секретный ключ, который мы придумали. Для начала с его помощью мы производим начальную перестановку значений в этом массиве.

В данном случае значением i будет являться индекс элементов по порядку от 0 до 255. А значением j будет выступать индекс массива, с которым мы элемент i поменяем местами. Чтобы этот j найти, мы складываем его с текущим элементом массива S и прибавляем к нему каждый следующий по порядку элемент ключа. При этом, чтобы не выйти за пределы ключа, если он окажется меньше 255 символов, мы поделим с остатком его текущий индекс на длину ключа.

По той же логике мы поделим с остатком полученное значение на 256, чтобы не выйти за пределы массива S. Теперь наша задача получить одно из этих значений, чтобы затем выполнить операцию XOR для первого байта исходных данных. Для этого мы заводим две переменные x и y, которые снова являются индексами массива S и которые после каждой обработки алгоритма будут хранить себе измененные индексы. В случае с x мы увеличиваем его на единицу и получаем индекс в рамках нашего массива. В случае с y мы прибавляем к нему новый полученный индекс x, и снова получаем одно из значений в рамках массива. В конце мы складываем два этих индекса между собой, получаем новый индекс и возвращаем значение, которое по этому индексу находится в массиве.

Только перед этим мы сразу поменяем значение под индексами x и y местами. В конце со создаем пустой массив, равный длине наших исходных данных, который будет хранить в себе конечный шифр. Далее перебираем байты исходного значения, для каждого байта получаем новый ключ, XOR`им его с текущим исходным байтом и результат шифрования записываем в новый созданный массив. Простота этого алгоритма позволяет ему в разы быстрее работать, чем блочный алгоритм DES. А благодаря тому, что шифрование основано всего лишь на одной операции XOR, расшифровка сообщения снова осуществляется этим же самым алгоритмом без каких-либо изменений. Мы получаем те же самые ключи, и применив операцию XOR в чётное количество раз, получаем исходное значение числа.

Безопасный обмен ключами

Итак, все необходимые алгоритмы для компьютеров были изобретены, и проблема с сокрытием информации наконец-то была решена. Казалось бы, на этой ноте можно было бы заканчивать нашу историю, если бы не одна маленькая проблема. Представьте, есть два компьютера в разных точках мира с установленным программным обеспечением DES. Первый компьютер зашифровывает своё сообщение и отправляет его второму. Второй, получив сообщение, бежит его скорее расшифровать, но тут же сталкивается со странной проблемой.

Где взять ключ? Отправить его по интернету, текстовым письмом или сообщить по телефону означает подвергнуть весь шифр максимальной уязвимости. А если отправителем будет необычный пользователь, до которого никому нет дела, а какой-нибудь крупный банк, отправляющий сообщения своему клиенту, то наверняка найдется много желающих это сообщение перехватить и использовать его в своих целях. Самый рабочий способ, которому тоже не особо можно доверять, это физически приехать к человеку и лично передать ему ключ прямо в руки.

Получается, весь этот технологический прогресс снова не в состоянии решить проблему средневековья. Когда посылали гонца передать важное сообщение лично в руки союзникам, им оставалось только надеяться, что самого гонца по пути никто не перехватит и сообщение действительно доедет в целостности.

Только теперь вместо гонцов отправлялись целые корабли, массово перевозящие криптографические ключи, записанные на перфокартах или дискетах. Если раньше шифрование использовалось только в основном в государственных и военных целях, то сейчас эта проблема приобрела массовость. В сокрытии информации стали нуждаться не только военные, но и весь остальной мир, включая всевозможные коммерческие организации. Поэтому физическая перевозка ключей была лишь временной мерой. Гонец это то самое слабое звено, которое ученым предстояло устранить.

Несмотря на то, что на протяжении всей истории утверждалось, что эта задача абсолютно неразрешима, уже в середине 70-х годов было найдено первое решение. Да, оно не было связано с компьютерами, но тем не менее она оказалась настолько простым и гениальным, что кажется невероятным, почему до этого никто не додумался раньше.

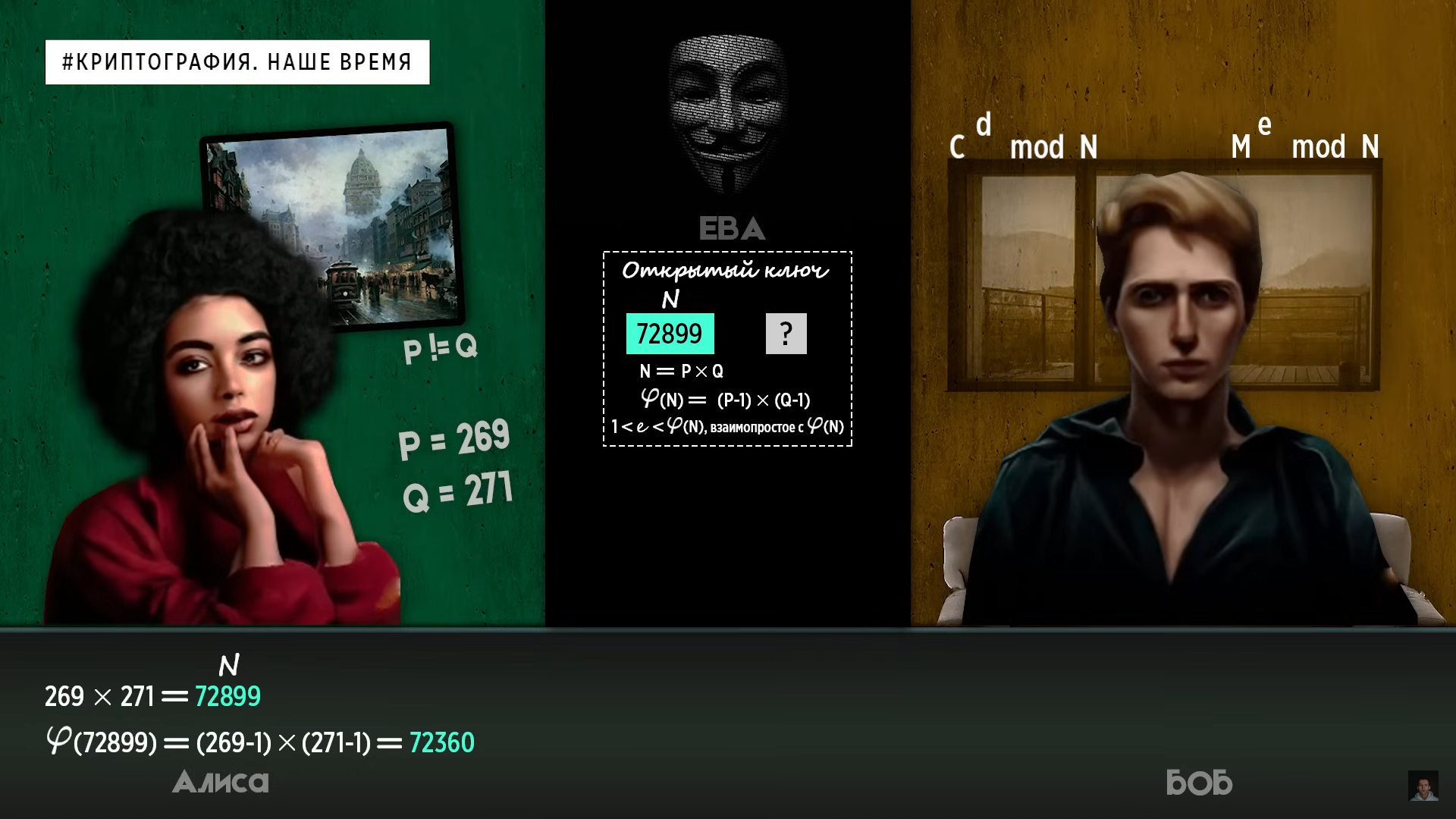
С этого момента в качестве участников для более удобного описания вводятся три абстрактных персонажа – Алиса, Боб и Ева. У которых, наверное, слышал каждый, кто хоть немного интересовался криптографией. Малисе нужно безопасно отправить свой ключ Бобу.

Что она делает? Она просто пишет на бумаге свой секретный ключ, кладет его в железный ящик, закрывает этот ящик своим физическим ключом на замок и отправляет этот ящик Бобу. Боб, получив ящик, разумеется, не может его открыть, так как у него нет ключа от замка Алисы.

Однако он ему и не нужен. Вместо попытки открыть этот замок, Боб просто навешивает на этот ящик собственный замок, закрывает его уже на свой физический ключ и отправляет этот ящик обратно Алисе. Алиса вновь получает свой отправленный ящик и снимает своим ключом свой замок, оставляя замок Боба нетронутым. После этого она во второй раз отправляет ящик Бобу, и тот без всяких проблем просто берет и открывает свой единственный оставшийся замок. Элементарно, скажете вы, и просто предложите заменить железный ящик зашифрованным сообщением. Однако в случае с компьютерами такое решение, к сожалению, не сработает.

Алиса зашифрует сообщение своим ключом, отправит его Бобу, Боб зашифрует уже зашифрованные данные своим ключом, и получится так, что передаваемое сообщение, в отличие от железного ящика, изменит свой внешний вид. А следовательно, ключ Алисы для снятия своего шифра уже не подойдет.

Несмотря на то, что историю с ящиком не удалось применить в цифровой отправке, она стала вдохновением для двух американских ученых Диффи и Хелмана. Которые в 1976 году представили алгоритм, позволяющий безопасно передавать ключи на любом расстоянии. Так как вместо символов мы теперь работаем с числами, то и мыслить нужно в рамках математики.

Дело в том, что математические функции обладают одной интересной особенностью. Они способны преобразовывать одно число в другое. Причем могут это делать не только в двустороннем порядке, но и в одностороннем. При котором восстановить исходное число будет довольно проблематично. Именно одна из таких односторонних функций вида G в степени x по модулю P и стала решением всех проблем.

Работает это так. Алиса и Боб абсолютно в открытую, любым удобным для них способом заранее договариваются о том, какими числами будут являться G и P при условии, что P и P-1 деленное на 2 будут простыми случайными числами. G будет первообразным корнем по модулю P. Например, в роли таких чисел подходят 7 и 11. При этом, чтобы посчитать формулу проверки первообразного корня, нужно понимать, что такое функция Эйлера, с которой мы подробно познакомимся чуть позже.

Главное преимущество существо обмена этими числами в том, что они не являются ни для кого тайной и могут быть без проблем перехвачены кем угодно. В отличие от числа x, которое уже является тайной и которое выбирается каждым участником индивидуально, не сообщая его друг другу. Например, Алиса в качестве x выбирает себе число 3, а Боб выбирает число 6. Таким образом, у каждого участника образуется своя собственная формула, которую каждый из них должен вычислить. Алиса получает 2, Боб получает 4. Эти два получившихся значения снова перестают являться какой-то тайной, и Алиса с Бобом снова без проблем в открытую ими обмениваются.

Зачем? А затем, что теперь каждый из них возьмет полученный друг от друга ответ, подставит его в свою формулу вместо G и получит одинаковое число 9, которое теперь и будет являться тем самым секретным ключом, с помощью которого Алиса и Боб будут зашифровывать и расшифровывать сообщения, передаваемые друг другу одним из алгоритмов вроде DES. Как мы видим, обмен состоялся благодаря одной лишь математике. Но как это возможно, если формулы были разными? На самом деле, разными они являются только на первый взгляд. Если копнуть чуть поглубже, можно увидеть, что они абсолютно идентичны.

Алиса получает от боба число 4. Число 4 это ничто иное, как 7 в шестой степени по модулю 11. Алиса берет это значение и возводит еще в свою третью степень. Боб же получает от Алисы число 2. Число 2 это 7 в третьей степени по модулю 11, которое Боб в виде готового значения возводит в свою шестую степень. Очевидно, что 7 в шестой в третьей степени это то же самое, что и 7 в третьей в шестой, так как от изменения степеней местами сам результат никак не изменится.

И вот в этот момент, когда стало все хорошо и прекрасно, на горизонте появляется третий персонаж, злоумышленник Ева. Она без проблем может перехватить все числа, которыми Алиса и Боб обменивались в открытую, но вот только воспользоваться нашей формулой она все равно не сможет, так как степень x каждого участника ей неизвестна. Ева просто попробует воспользоваться старым добрым методом перебора, пока формула не выдаст число 9.

К счастью Евы, это произойдет меньше, чем за секунду, так как в примере использовались очень маленькие значения. Для обеспечения защиты от подобного взлома в качестве X требуется выбирать огромные числа, на перебор которых уйдет не менее огромное количество времени. Да, это действительно решает проблему с полным перебором, но тут же создает новую проблему с возведением числа в огромную степень.

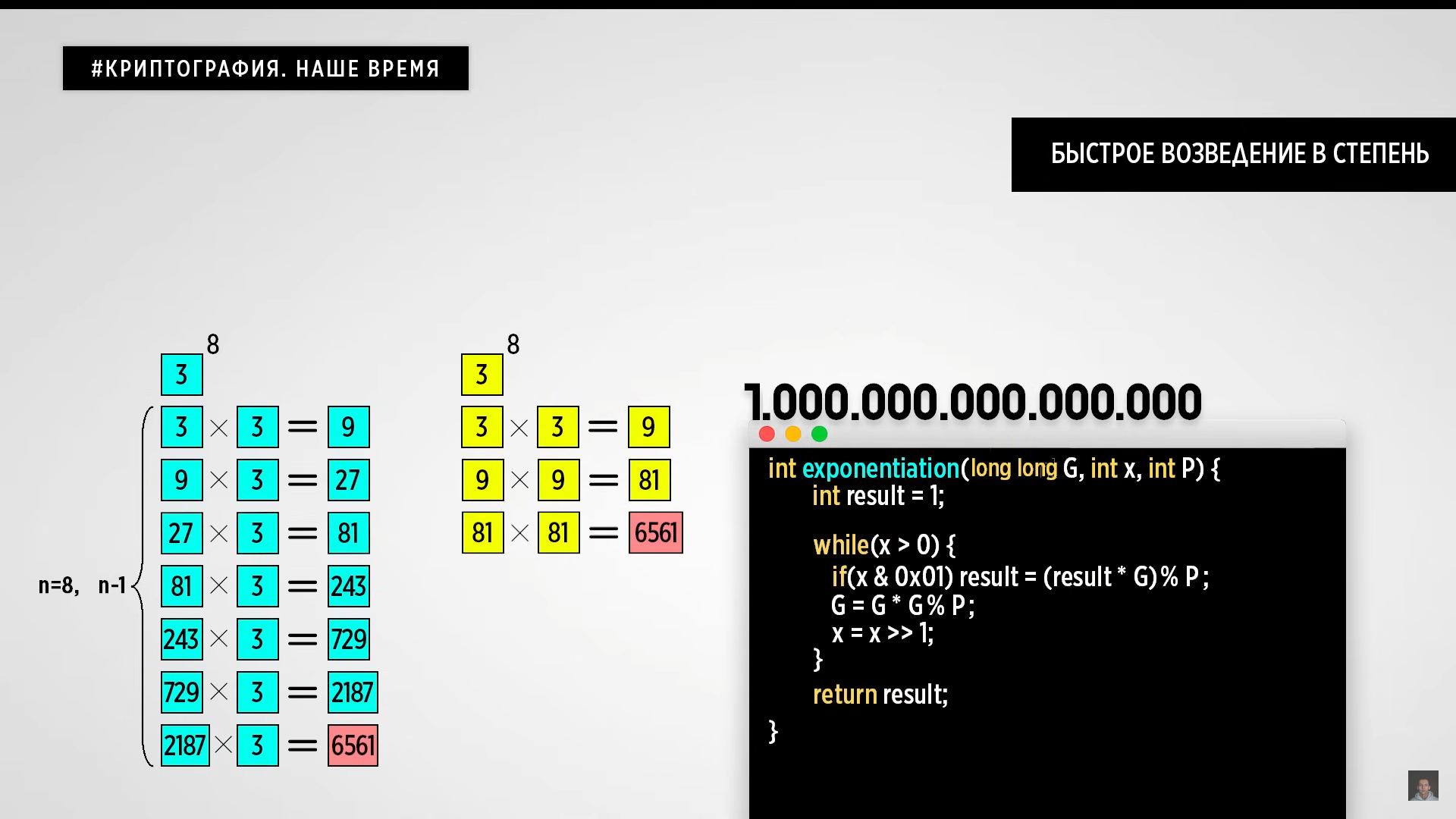
Постоянное перемножение его друг на друга N-1 раз – это очень медленный способ, особенно если представить, что в роли N будет выступать не число 8, а число квадриллион. Чтобы оптимизировать это вычисление, можно пойти немного другим путем. Вместо полного перемножения чисел друг на друга, мы будем сохранять промежуточные результаты, возводя их в степень 2.

Чтобы перенести эту идею на код, можно воспользоваться особенностями битовых операций. Мы заводим некую переменную result со значением единица, которая в ходе изменений станет нашим ответом, который мы в конце функции и вернем. Посередине же будет крутиться цикл до тех пор, пока наша степень x будет больше нуля. Это означает, что внутри цикла мы должны будем ее потихоньку уменьшать. Уменьшать мы ее будем за счет постоянного деления на 2, что является аналогом правого сдвига на единицу. При этом на каждой в итерации цикла мы должны будем проверять самый младший бит этой степени. Если он будет равен 1, значит мы перезаписываем результат путем умножения его на G. Далее мы просто возводим G в квадрат путем перемножения его самого на себя. Все, что осталось сделать, это добавить остаток от деления на P, и в итоге возведение числа в степень ускорится в несколько раз.

Хорошо. Ева, конечно же, ждать долгие годы окончания перебора не будет, а пойдет немного другим путем. Кроме обычного перехвата значений ей доступна привилегия их подменять. Например, вместо реальных чисел А и Б, которые сформировали Алиса и Боб, Ева подставит число 1. Это приведёт к тому, что как Алиса, так и Боб станут возводить единицу в свои скрытые степени, в результате чего получат секретный ключ в виде числа 1, о котором теперь будет известно всем трём участникам. Конечно, Алиса и Боб не настолько глупы, чтобы попасться в такую ловушку и просто заранее станут проверять, не равно ли передаваемое значение 1. Хорошо, в очередной раз ответит Ева, и пойдет более сложным, но более безопасным для нее путем.

Она просто возьмет и придумает два своих секретных числа x1 и x2. Затем по известной всем формуле получит свои числа c и d и станет ждать. В момент, когда Алиса будет передавать Бобу свое число А, Ева его перехватит, сохранит, подменит на свое число С и отправит Бобу.

Когда Боб на основе этого числа получит свое число B и отправит его Алисе, Ева перехватит это число, снова сохранит, подменит на свое число D и отправит Алисе. Таким образом, и Алиса, и Боб обменяются секретными ключами с Евой, думая, что обменялись между собой. Теперь, когда Алиса пошлет Бобу свое зашифрованное сообщение, Ева его перехватит, расшифрует секретным ключом Алисы, внесет в него при необходимости некоторые изменения, зашифрует секретным ключом Боба и отправит ему это сообщение.

Вдобавок к этой уязвимости есть еще одна неприятная проблема, делающая этот алгоритм далеко не самым практичным. Алиса не сможет послать сообщение Бобу по интернету ровно до тех пор, пока и Боб и Алиса одновременно не появятся в сети, чтобы сформировать общий секретный ключ.

Конечно, Алиса просто могла заранее разместить свои числа G, P и A в открытом доступе, и тогда бы каждый мог в любое время на основе этих чисел шифровать и отправлять Алисе сообщение вместе со своим числом B. Однако в таком бы случае Алисе пришлось каждый раз генерировать новый закрытый ключ для каждого своего собеседника и только после этого расшифровывать его сообщение.

RSA

Хоть обмен ключами и стал возможен, неудобств здесь по-прежнему хватало. К счастью, Диффи быстро понял, что все эти неудобства с обменами кроются лишь в одинаковом ключе. Дело в том, что все существующие на тот момент алгоритмы были симметричными, то есть использовали один и тот же ключ как для шифрования сообщения, так и для расшифрования. Именно эта особенность алгоритма и вынуждает как отправителя, так и получателя постоянно рисковать, обмениваясь ключом. Думая обо всём этом, в голове Диффи родилась совершенно безумная и, как тогда казалось, неосуществимая идея. Что если Алиса вместо одного закрытого ключа создаст два абсолютно разных? Первый ключ будет использоваться для шифрования сообщения. Он будет находиться в открытом доступе для всех тех, кто захочет передать Алисе свое сообщение.

А второй ключ будет храниться Алисой в тайне. И будет использоваться для расшифрования всех полученных сообщений. То есть шифрование станет асимметричным.

Как это сделать, Дифи на тот момент вообще не догадывался. Поэтому его идея так и оставалась чем-то фантастически в различных научных статьях, пока знакомый нам учёный Рональд Ревест не наткнулся на одну из его статей. Если кто-то способен сгенерировать идею, которая должна перевернуть мир, то обязательно найдутся люди, которые попытаются воплотить её в жизнь.

С этого момента Рональд вместе со своим коллегой Леонардом Адлеманом загорелись идеей найти такую одностороннюю математическую функцию, которая бы полностью удовлетворяла идее асимметричного шифра. Впоследствии к ней присоединился Адиша Мир. Трое были учеными Массачусетского института. Бревест и Шамир были специалистами в области теории вычислительных машин и периодически генерировали идеи по реализации такого шифра. Адлеман же был математиком.

И в течение целого года в пух и прах разбивал все предложенные идеи, находя в них различные слабые места и уязвимости, пока в один из апрельских дней 1977 года Бревест, Шамир и Адлеман не отмечали еврейскую пасху, выпивая много вина. После того, как друзья разошлись, Рональд долго не мог уснуть, размышляя об асимметричном шифре. Поэтому он не придумал ничего лучше, как посреди ночи взять учебник по математике и начать его читать. Именно в этот момент его посетило откровение. Весь остаток ночи он посвятил доработке своей идеи, и уже к утру научная статья по симметричному шифрованию была полностью готова. Когда Ревест встретил Адлемана и показал ему эту статью, тот, как обычно, попытался найти в ней какие-то ошибки. Однако на сей раз сделать этого ему не удалось. Алгоритм решили назвать по первым буквам трех ученых. Привет, Шамир Адлиман.

Алгоритм RSA стал важнейшим открытием в криптографии и, можно сказать, полностью перевернул весь мир. При этом, если мы взглянем на общую формулу шифрования и расшифрования, то вообще не увидим никаких отличий от формулы Диффи Хелмана. Секрет успеха заключается в самом методе нахождения всех этих чисел. Главным оружием математики во всем этом оказались простые числа. Но если конкретнее, то отсутствиена сегодняшний день быстрого способа разложения чисел на простые множители. Только если вновь методом перебора не будем проверять, не делится ли это число без остатка на каждое из простых чисел. Как обезоружить такой метод, мы уже знаем. Нужны огромные числа. Мы же для удобства восприятия рассмотрим пример на маленьких числах.

Вначале Алиса выбирает два случайных простых числа P и Q, не равных друг другу, и перемножает их между собой. Ответ N, который она получит, будет являться первой частью открытого ключа, который она затем опубликует в интернете. Вторая часть закрытого ключа будет выбрана на основе результата функции Эйлера от полученного числа N. Эта функция показывает, сколько натуральных чисел от 1 до N-1 включительно являются взаимопростыми.

Для этого мы, конечно же, можем перебирать все числа от 1 до N-1, для каждого числа проверять, нет ли у них с N общих делителей, кроме единицы, и вернуть количество найденных взаимопростых с N чисел. Однако такой способ вычисления снова будет являться очень долгим при использовании больших P и Q. Поэтому данное вычисление мы можем заметно упростить, представив его как произведение F от P умноженное на F от Q.

Однако мы можем заметить, что если N было простым числом то ответ всегда будет давать число N-1. Это означает, что мы сразу можем упростить это вычисление до формулы p-1 умноженное на Q-1. Окей. Теперь на основе этого числа нам нужно выбрать открытую экспоненту, которая будет являться вторым целым числом открытого ключа. Оно должно быть простым, находящимся в диапазоне от 1 до F от N, и быть взаимопростым с этим значением. Причем желательно, чтобы это было такое число, у которого в двоичном виде будет очень мало единиц. Почему? Потому что это число, как мы увидим далее, будет использовано в качестве степени для шифруемого сообщения. Но как мы помним из алгоритма быстрого возведения в степень, чем меньше единиц в двоичном представлении степени, тем быстрее происходит вычисление.

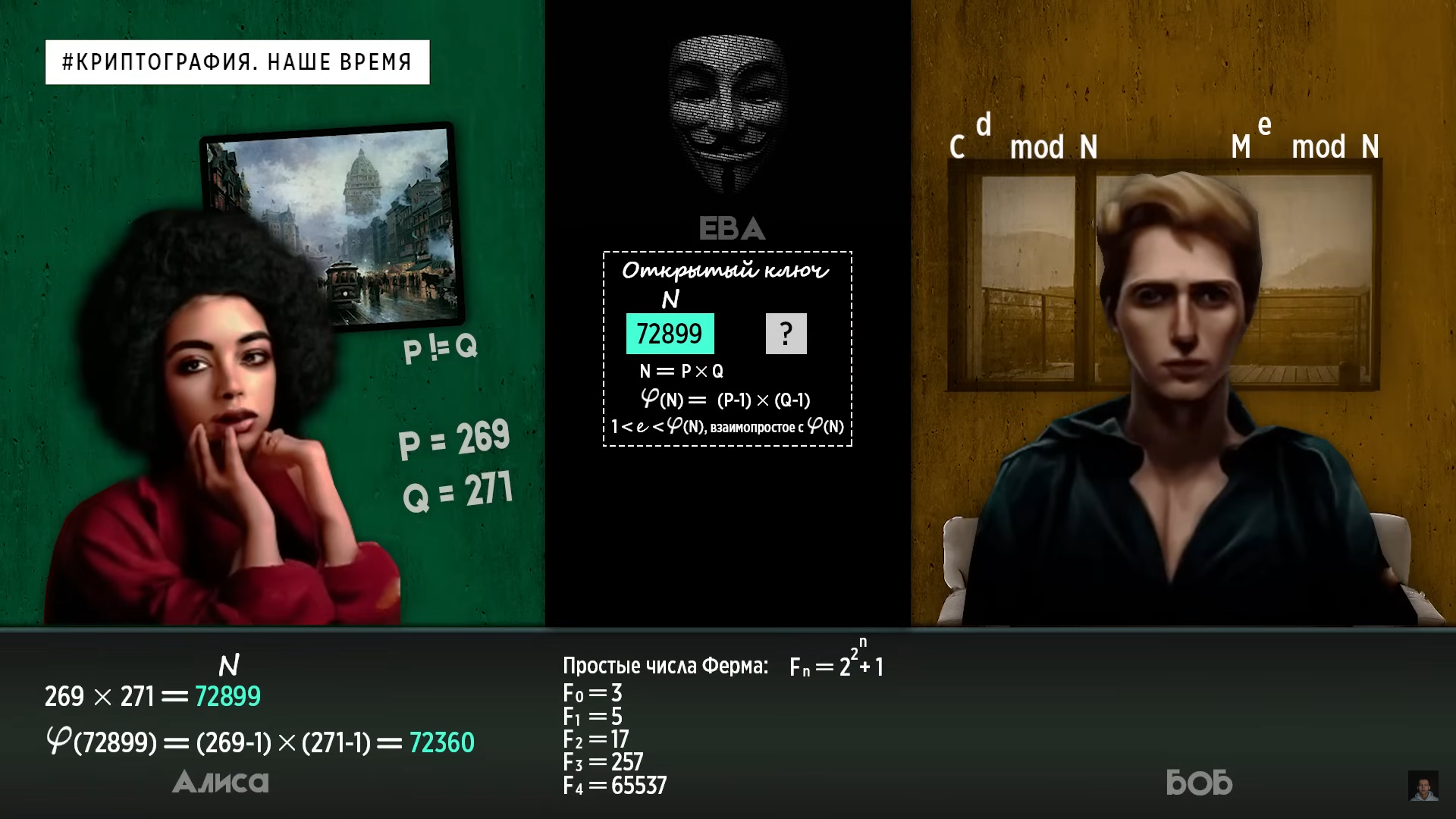
Так вот, оказалось, что в качестве такого числа идеально подходит одно из простых чисел Ферма. Вычисляются они по формуле 2 в степени 2 в степени N+1. Если вместо N мы начнем подставлять числа, начиная с нуля, то получим следующий ряд.

Однако после пятого числа в этой последовательности числа становятся составными, то есть появляется способ разложения их на множители. А из оставшейся пятерки первые два являются слишком маленькими, что в теории может породить дополнительную уязвимость. Поэтому для примера мы выберем число 65537. Глядя на его двоичный вид, становится очевидным, почему оно идеально подходит.

			1 0000 0000 0000 0001
		

Всего две единицы в начале и в конце и 15 нулей посередине. Именно эти два числа теперь будут являться нашим открытым ключом, с помощью которого сообщение можно зашифровать. Осталось генерировать закрытый ключ, который позволит нам его расшифровать. Для этого нам всего лишь нужно вычислить закрытую экспоненту.

Проще говоря, это такое число, которое при умножении на e по модулю F от N даст единицу. Как правило, вычисляется оно по расширенному алгоритму Евклида. Стандартный алгоритм Евклида позволяет найти наибольший общий делитель двух натуральных чисел A и B. Мы просто делим B с остатком на A и вызываем рекурсию, меняя числа местами. То есть в качестве A мы передаем изменённый B, а в качестве B – текущий A. Таким образом, аргумент A на каждом рекурсивном вызове будет уменьшаться ровно до тех пор, пока наш остаток отделения не станет равным нулю. Именно в тот момент, когда это произойдет, в переменной B и будет находиться наибольший общий делитель. Хорошо, если мы немного расширим этот алгоритм, то помимо наибольшего общего делителя, сможем найти так называемые коэффициенты x и y.

Причем такие, что если мы впоследствии A умножим на x и прибавим к этому B умноженное на y, то снова получим этот же самый наибольший делитель, который только что находили. Однако конкретно сейчас нас это не интересует. Нас интересует только коэффициент x. Дело в том, что именно он и станет тем самым вторым числом закрытого ключа в том случае, если этот x окажется положительным. Если он окажется отрицательным, то для получения второго числа закрытого ключа нам потребуется сложить этот отрицательный x с результатом функции F от N. Ну окей. Осталось понять, как этот коэффициент найти.

Кроме чисел A и B мы передаем функции ссылки на x и y, в которой и запишутся значения коэффициента. Так как нам нужно кроме общего делителя возвращать промежуточные значения x и y на каждом этапе скрутки рекурсии, то мы на каждом вызове будем заводить свои x1 и y1, которые будут передаваться в следующий вызов. В итоге получится, что у каждого кадра стека будет свой x и y, которым будет сохраняться доступ у нижестоящего кадра за счет переменных x1 и y1.

В конце каждого вызова мы будем брать x1 и y1 из предыдущего кадра и перезаписывать наши текущие x и y следующим образом. Результат деления B на A мы умножаем на x1 и все это вычитаем из y1. Это у нас x, y же просто будет перезаписываться на предыдущий x. В итоге в этом примере мы получим значения минус 1 и 1. В нашем же примере с Бобом и Алисой мы получим x равный 13193.

Число положительное, поэтому оно сразу будет являться вторым числом D нашего закрытого ключа. Таким образом, пара чисел N и D будут являться нашим секретным ключом для расшифровки полученных сообщений.

Как теперь применить это на практике? Чтобы зашифровать, берем нашу формулу, исходное сообщение M и открытый ключ. Вместо G подставляем M, вместо степени подставляем e, вместо модуля подставляем N.

Получаем зашифрованное сообщение C, которое с помощью этой же формулы и закрытого ключа мы можем расшифровать. Вместо G подставляем C, вместо степени D, а вместо модуля снова число N.

Когда описание этого алгоритма было опубликовано в массы, вместе с ним людям было предложено за 100 долларов расшифровать такую вот последовательность чисел, которая является зашифрованной английской фразой. Открытым ключом здесь выступала N, состоящая из 425 бит и открытой экспонента 9007. Рональд предполагал, что на взлом уйдет около 40 квадриллионов лет. Рональд немного ошибся. Через 15 лет, 3 сентября 1993 года, шифр был взломан. Это оказалась фраза «The Magic Words are Squeamish Ossifrage».

Взлом удался благодаря проекту распределённых вычислений, в котором 600 добровольцев из 20 стран одновременно предоставляли свои вычислительные ресурсы. 425 бит для безопасности оказалось очень мало. Вычислительные мощности постоянно растут, но вместе с ним растут и количество бит-числа, которые делают его безопасным от взлома перебором. На данный момент такое число начинается от 2048 бит. Но нужно понимать, что всё равно существуют две ситуации, при которых алгоритм RСА моментально отправится в мусорку.

Первый — это если кто-то рано или поздно всё-таки найдёт быстрый способ разложения чисел на простые множители.

Второй — кто-то рано или поздно всё-таки изобретёт квантовый компьютер, который даст немыслимую для современных суперкомпьютеров скорость вычисления, которая выведет человечество в совершенно новую реальность.

Но пока этого не произошло, вся информация актуальна, поэтому двигаемся дальше. Асимметричные алгоритмы с открытым ключом позволили воплотить в жизнь такую технологию, как цифровая подпись. Позволили всем нам безопасно пользоваться интернетом, совершать покупки, отправлять личные данные, например, для входа в аккаунт, отправлять файлы, личные сообщения и так далее.

Все это делается браузером автоматически, поэтому такие вещи мы, как правило, привыкли не замечать, считая это чем-то само собой разумеющимся. Спустя несколько десятилетий криптографы снова вырвали победу у криптоаналитиков, но это означает только одно. Очередь перевернуть игру теперь за ними. На протяжении веков любые шифры, которые считались абсолютно стойкими, всегда падали под натиском желания людей раскрыть тайное. Поэтому можно однозначно гарантировать, что любой неуязвимый на сегодняшний день шифр рано или поздно будет раскрыт.

Новый стандарт шифрования AES

Если на этом моменте вы снова подумали, что история закончилась и видео подошло к концу, то спешу вас огорчить. Раскрываться шифры начнут прямо сейчас, даже не дожидаясь окончания видео. Первым на очереди оказался DES, который спустя 21 год своего существования уже в 1998 году дал первую и последнюю трещину.

В этом году было проведено масштабное исследование с целью взломать данный алгоритм, в результате чего за 250 тысяч долларов был построен суперкомпьютер, который смог выполнить расшифровку методом перебора менее чем за три дня. Всем было очевидно, что то, что считается суперкомпьютером сегодня, через 5-10 лет будет обыкновенным ПК в доме каждого школьника. Поэтому для увеличения криптостойкости DES, а конкретно для устранения атаки методом полного перебора, были предприняты попытки немного видоизменить этот алгоритм, в результате чего появились его модификации. Например, 3DES, в котором использовалось три ключа, и вместо одного шифрования выполнялось три по принципу матрёшки. Этот способ замедлял скорость исходного алгоритма ровно в три раза.

Поэтому появлялись новые модификации. Например, DESX, в которой исходные данные перед шифрованием, а затем конечные данные после шифрования, XOR`ились с дополнительными 64-битными ключами. Оба способа позволяли, грубо говоря, увеличить исходный 56-битный ключ до 168 и 184 бит соответственно. Благодаря чему они даже нашли применение в электронных почтах, продуктах компании Microsoft и даже в платежных системах.

Однако любой костыль способен прослужить лишь незначительное время. Мир снова нуждался в изобретении чего-то нового, но уже не по вине развития человеческих возможностей, а по вине самого человека, который стремится контролировать всё и вся. По этой причине в 90-х годах начинают появляться всё больше и больше блочных алгоритмов, поставленных на сети Фейстеля по примеру успеха DES, но только без той самой уязвимости маленького ключа. Чтобы из всего этого многообразия выбрать приемника, потребовался еще один конкурс, в результате которого в 2000 году в качестве победителя был объявлен алгоритм RINDAEL. Именно он стал новым расширенным стандартом шифрования с аббревиатурой AES. Однако, несмотря на продемонстрированную надежность сети Фейстеля, этот алгоритм снова вернулся к идее использования SP-сети, с которой когда-то начинался отец блочных алгоритмов Люцифер. И то, и другое является способом организации блочных алгоритмов.

Работает AES следующим образом. Блоки исходного сообщения и ключ теперь составляют по 128 бит. Все эти 16 байт мы разбиваем на матрицу 4х4 сверху вниз и XOR`им каждый байт из матрицы исходного сообщения соответствующим байтом матрицы ключа. В данном алгоритме это удобнее делает 16-тиричной системе счисления и дальше мы поймем почему.

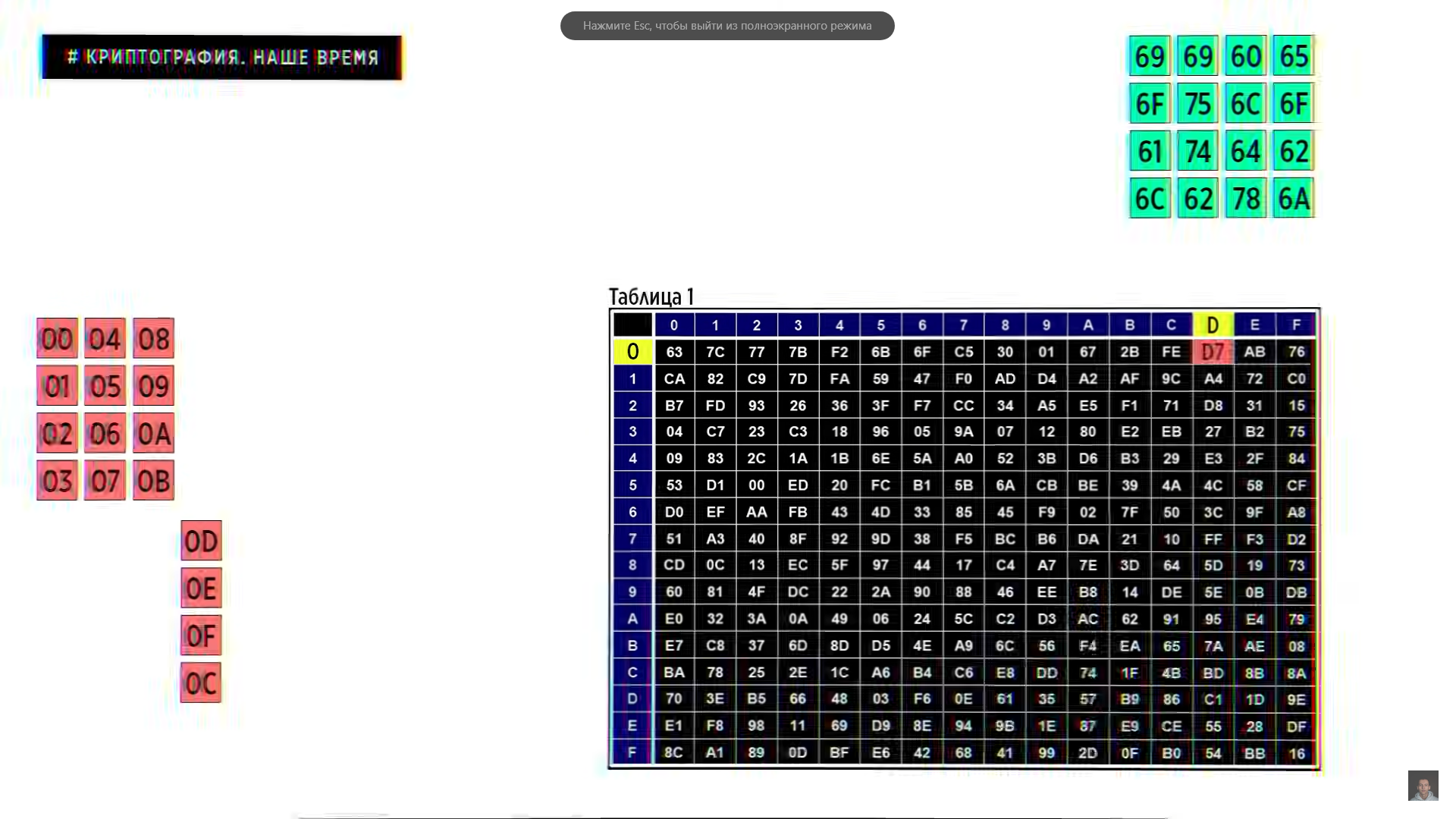
Здесь нам предстоит выполнить 10 одинаковых раундов, но перед тем как мы это сделаем, нам снова потребуется разбить исходный ключ на 10 ключей для каждого раунда. Для этого мы берем четвертую колонку из матрицы, переставляем первый элемент в самый конец и производим замену каждого байта согласно таблице 1. Чтобы это сделать, разбиваем каждый байт по 4 бита.

Таким образом получится, что первая цифра 16-ричного числа будет обозначать номер строки, а вторая цифра — номер колонки. На пересечении строки и колонки и находится байт для замены. Измененную четвертую колонку мы XOR`им с первой колонкой, затем с колонкой для первого раунда из таблицы 2. То, что получилось, является первой колонкой матрицы ключа первого раунда. Выполнив XOR этой колонки со второй колонкой исходного ключа, мы получаем вторую колонку первого раунда. XOR`им её с третьей колонкой исходного ключа, чтобы получить третью колонку, и XOR`им её с четвёртой колонкой исходного ключа, чтобы получить четвёртую колонку. Матрица ключа первого раунда готова.

На основе этой матрицы формируется матрица ключа второго раунда точно по такому же алгоритму. Каждый основной раунд, кроме последнего, состоит из четырех шагов. Вначале мы по таблице 1 производим замену байтов, как это было с ключом. Затем производим циклические сдвиги влево на уровне байтов строк матрицы. Первая строка сдвигается на 0, вторая на 1, третья на 2 и четвертая на 3.

Третий шаг выполняется для всех раундов, кроме 10. В нем и каждый столбец нашей матрицы должны умножить на каждую строку матрицы следующего вида. Подвох в том, что это совершенно не то умножение, которому мы привыкли. Чтобы его произвести, нужно все наши числа представить в двоичном виде, чтобы затем сформировать из них полином, где степень х обозначает индекс бита, в котором была единица. Далее мы уже, как обычно, перемножаем два полинома между собой и снова собираем из них число в двоичном виде. Этот результат не должен выходить за пределы одного байта.

То есть он не может быть больше, чем 255. Однако мы видим, что некоторые значения вылезли за этот предел. В таком случае мы применяем к ним дополнительный XOR и получаем итоговый результат.

Последний шаг это выполнить XOR получившейся матрицы с матрицей ключа первого раунда и отправить всю эту матрицу в раунд второй.

Следом за DES посыпался и RC4. В начале 2000-х было доказано, что первые байты генерируемого ключа коррелируются с первыми байтами обычного ключа. Это создает вероятность того, что используемый ключ может быть раскрыт. Поэтому алгоритм тоже признается устаревшим, и на смену ему создается множество всевозможных поточных алгоритмов, а генераторы псевдослучайных чисел активно находят свое применение не только в криптографии, но и в компьютерных играх, лотереях и так далее. Шифры продолжают появляться и продолжают умирать. Война криптографов с криптоаналитиками бесконечна, и нам остается лишь наслаждаться этой математической битвой лучших умов планеты.

Мы уже писали про алгоритмы шифрования. Если хотите больше погрузиться в тему, можете почитать:

Тут про наборы шифров: ROT1, азбуку Морзе, шифр Цезаря, моноалфавитную замену, шифр Энигмы и прочее.

С примерами, которые нужно будет расшифровать.

Если вам понравилась история про Алису, Боба и Еву — то в этой статье приведён код на Python, который решает проблему передачи ключей.

Название заметки говорит само за себя — коротко рассказываем, в чём суть этих терминов и где они отличаются.