На пути к Deep Blue: пошаговое руководство по созданию простого ИИ для игры в шахматы

Рассмотрим некоторые базовые концепции, которые помогут нам создать простой искусственный интеллект, умеющий играть в шахматы:

• перемещение;
• оценка шахматной доски;
• минимакс;
• альфа-бета-отсечение.

На каждом шаге мы будем улучшать наш алгоритм с помощью одного из этих проверенных временем методов шахматного программирования. Вы увидите, как каждый из них влияет на стиль игры алгоритма.

Готовый алгоритм можно найти на GitHub.

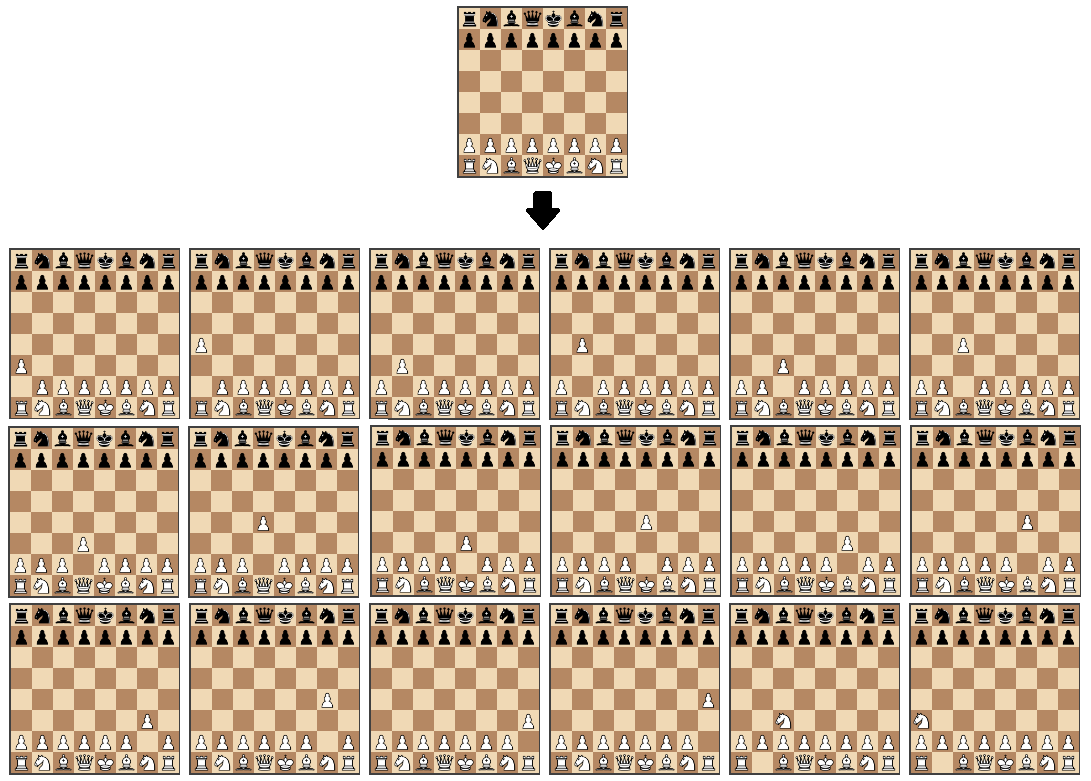
Шаг 1. Генерация ходов и визуализация шахматной доски

Мы будем использовать библиотеки chess.js для генерации ходов и chessboard.js для визуализации доски. Библиотека для генерации ходов реализует все правила шахмат. Исходя из этого, мы можем рассчитать все ходы для данного состояния доски.

Использование этих библиотек поможет нам сосредоточиться только на самой интересной задаче — создании алгоритма, который находит лучший ход. Мы начнем с написания функции, которая возвращает случайный ход из всех возможных ходов:

			var calculateBestMove = function(game) {
    //Генерация всех ходов для данной позиции
    var newGameMoves = game.ugly_moves();
    return newGameMoves[Math.floor(Math.random() * newGameMoves.length)];
};
		

Хотя этот алгоритм не очень солидный шахматист, но это хорошая отправная точка, поскольку его уровня достаточно, чтобы сыграть с нами:

Посмотреть, что получилось на данном этапе, вы можете на JSFiddle.

Шаг 2. Оценка доски

Теперь попробуем понять, какая из сторон сильнее в определенном положении. Самый простой способ добиться этого — посчитать относительную силу фигур на доске, используя следующую таблицу:

С помощью функции оценки мы можем создать алгоритм, который выбирает ход с наивысшей оценкой:

			var calculateBestMove = function (game) {

    var newGameMoves = game.ugly_moves();
    var bestMove = null;
    //Используйте любое отрицательное число
    var bestValue = -9999;

    for (var i = 0; i < newGameMoves.length; i++) {
        var newGameMove = newGameMoves[i];
        game.ugly_move(newGameMove);

        //Возьмите отрицательное число, поскольку ИИ играет черными
        var boardValue = -evaluateBoard(game.board())
        game.undo();
        if (boardValue > bestValue) {
            bestValue = boardValue;
            bestMove = newGameMove
        }
    }

    return bestMove;

};
		

Единственным ощутимым улучшением является то, что теперь наш алгоритм съест фигуру, если это возможно:

Посмотреть, что получилось на данном этапе, вы можете на JSFiddle.

Шаг 3. Дерево поиска и минимакс

Затем мы создадим дерево поиска, из которого алгоритм может выбрать лучший ход. Это делается с помощью алгоритма «минимакс».

Прим. перев. В одной из наших статей мы уже имели дело с минимаксом — учились создавать ИИ, который невозможно обыграть в крестики-нолики.

В этом алгоритме рекурсивное дерево всех возможных ходов исследуется до заданной глубины, а позиция оценивается на «листьях» дерева.

После этого мы возвращаем либо наименьшее, либо наибольшее значение потомка в родительский узел, в зависимости от того, чей просчитывается ход (то есть мы стараемся минимизировать или максимизировать результат на каждом уровне).

			var minimax = function (depth, game, isMaximisingPlayer) {
    if (depth === 0) {
        return -evaluateBoard(game.board());
    }
    var newGameMoves = game.ugly_moves();
    if (isMaximisingPlayer) {
        var bestMove = -9999;
        for (var i = 0; i < newGameMoves.length; i++) {
            game.ugly_move(newGameMoves[i]);
            bestMove = Math.max(bestMove, minimax(depth - 1, game, !isMaximisingPlayer));
            game.undo();
        }
        return bestMove;
    } else {
        var bestMove = 9999;
        for (var i = 0; i < newGameMoves.length; i++) {
            game.ugly_move(newGameMoves[i]);
            bestMove = Math.min(bestMove, minimax(depth - 1, game, !isMaximisingPlayer));
            game.undo();
        }
        return bestMove;
    }
};
		

С минимаксом наш алгоритм начинает понимать основную тактику шахмат:

Посмотреть, что получилось на данном этапе, вы можете на JSFiddle.

Эффективность минимакса в значительной степени зависит от достижимой глубины поиска. Именно это мы улучшим на следующем шаге.

Шаг 4. Альфа-бета-отсечение

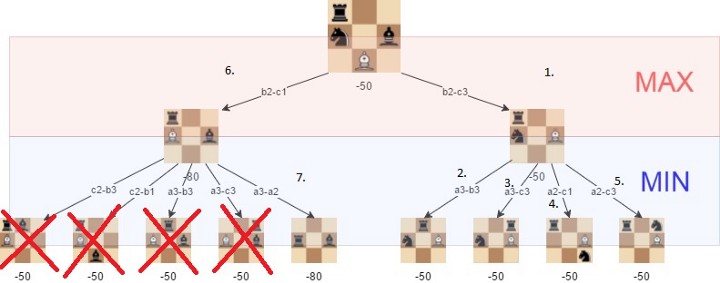
Альфа-бета-отсечение — это метод оптимизации алгоритма «минимакс», который позволяет игнорировать некоторые ветви в дереве поиска. Это позволяет нам намного глубже оценить дерево поиска, используя те же ресурсы.

Альфа-бета-отсечение основано на ситуации, когда мы можем прекратить оценивать часть дерева поиска, если найдем шаг, который приведет к худшей ситуации, чем та, к которой приводил ранее обнаруженный шаг.

Альфа-бета-отсечение не влияет на результат минимакса, оно только ускоряет его.

Этот алгоритм будет более эффективным, если мы сначала проверим те пути, которые ведут к хорошим ходам:

С альфа-бета-отсечением мы получаем значительное улучшение минимакса, как показано в следующем примере:

Посмотреть, что получилось на данном этапе, вы можете на JSFiddle.

Шаг 5. Улучшенная функция оценки

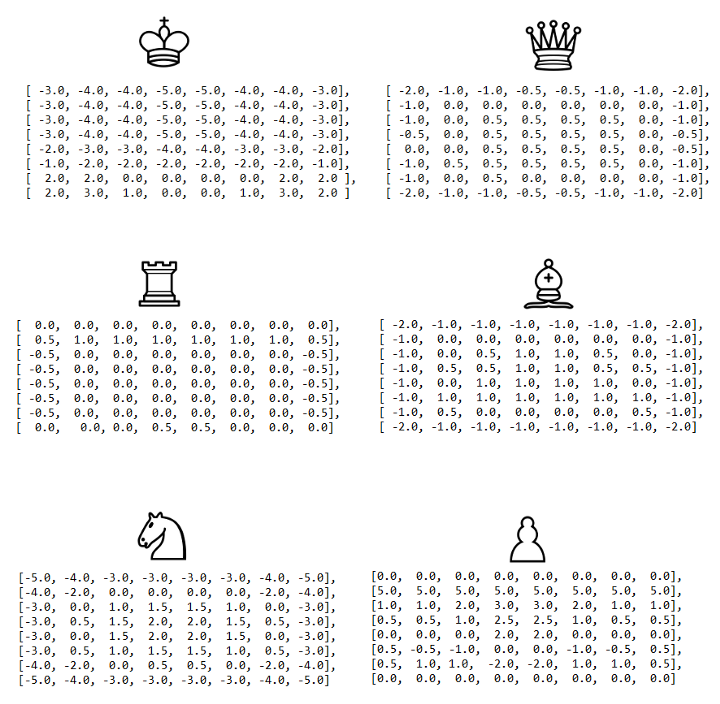
Первоначальная функция оценки довольно наивна, поскольку мы просто подсчитываем очки фигур, которые находятся на доске. Чтобы улучшить её, мы начнём учитывать положение фигур. Например, конь в центре доски «дороже», потому что он имеет больше доступных ходов и, следовательно, более активен, чем конь на краю доски.

Мы будем использовать слегка скорректированную версию квадратных таблиц, первоначально описанных в вики Chess Programming.

Применив это улучшение, мы получим алгоритм, который неплохо играет в шахматы, по крайней мере, с точки зрения простого игрока:

Посмотреть, что получилось на данном этапе, вы можете на JSFiddle.

Заключение

Сила даже простого шахматного алгоритма состоит в том, что он не совершает глупых ошибок. Тем не менее, ему по-прежнему не хватает стратегического взгляда на ситуацию.

С помощью методов, которые представлены здесь, мы смогли запрограммировать шахматный алгоритм, который может неплохо играть в шахматы. В финальном алгоритме реализация ИИ занимает всего 200 строк кода — это означает, что базовые принципы довольно просты. Вы можете посмотреть окончательную версию программы на GitHub.

Вот некоторые дополнительные улучшения, которые мы могли бы внести в алгоритм:

• упорядочивание ходов;
• ускорение генерации ходов;
• оценка эндшпиля.

Если вы хотите узнать о шахматных алгоритмах больше, зайдите на Chess Programming Wiki.