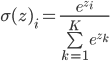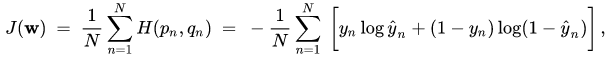Практикум: машинное обучение в медицине на примере CNTK от Microsoft

В предыдущем гайде мы построили простую сеть и решили задачу построения оператора XOR. Имея понимание того, как работает модель из предыдущей задачи, можно переходить к более сложным задачам. Давайте рассмотрим задачу классификации на примере нескольких абстрактных заболеваний — A, B, C, D, E.

Структура:

• Задача классификации (мультикласс, немного теории);
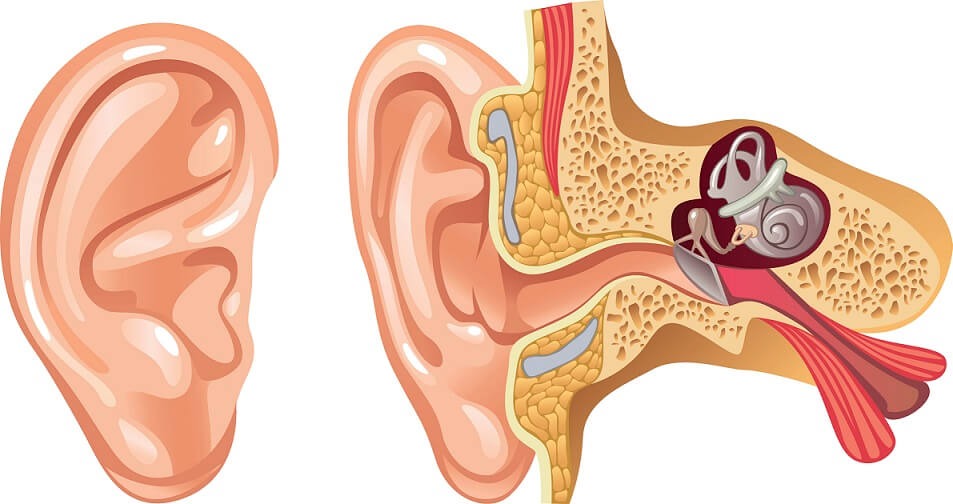
• Задача диагностики ушных заболеваний;
• Причесывание датасета;
• Конфигурация сети в 2 варианта – SoftMax и Sigmoid;
• Сравнение результатов, приведение ответов сети к полному вероятностному пространству.

Матчасть

Выделяют 3 основных типа задач классификации:

1. Бинарная классификация (Есть положительный и отрицательный признак).
2. Multiclass classification (Объект носит признаки исключительно одного класса).
3. Multilabel classification (Объект имеет признаки нескольких классов одновременно).

Рассмотрим 3 примера на каждый тип задач:

1. Определение наличия у человека некой болезни Х. 1 – человек болен, 0 – человек здоров.
2. Определение одной болезни среди болезней A, B, C, D, E.
3. Определение нескольких болезней среди A, B, C, D, E.

Вопрос теперь в том, в чем будет разница выходного вектора. Для бинарной классификации мы можем использовать скалярные значения. Болен – 1, здоров – 0.

Теперь, когда у нас есть 5 болезней – A, B, C, D, E, – мы должны их представить в каком-то адекватном формате. Есть 2 способа кодирования переменных номинального типа: Label Encoding и One Hot Encoding.

Если использовать Label Encoding, A, B, C, D, E превратятся в 0, 1, 2, 3, 4. Так можно кодировать некоторые переменные, спору нет (особенно переменные ординального типа, отдельно про типы переменных читаем здесь и здесь), но в случае классификации – не стоит. Сеть определенно испытает трудности в процессе обучения, а вы – в интерпретации ответа 3,5.

Поэтому по старинке используем One Hot Encoding и получаем следующее:

A - [1, 0, 0, 0, 0]B - [0, 1, 0, 0, 0]C - [0, 0, 1, 0, 0]D - [0, 0, 0, 1, 0]E - [0, 0, 0, 0, 1]

i-ая компонента вектора указывает на вероятность наличия класса i у объекта. Вернемся к тому же ответу вида 3,5. Его можно понимать как то, что у человека что-то среднее между болезнью D и Е. В случае One Hot Encoding вектор будет иметь следующий вид:
[ 0.05, 0.03, 0.1, 0.42, 0.49 ]

От теории к практике

Раз уж разговор зашел о медицине, давайте решим задачу диагностики ушных заболеваний. Здесь будет интересна даже не сама задача, а те подводные камни, с которыми вы наверняка столкнетесь. Итак, датасет можно взять здесь.

Датасет небольшой, тем не менее, у него есть интересные особенности:

• Содержит переменные только номинального/ординального типа;
• Входной вектор имеет довольно большую размерность;
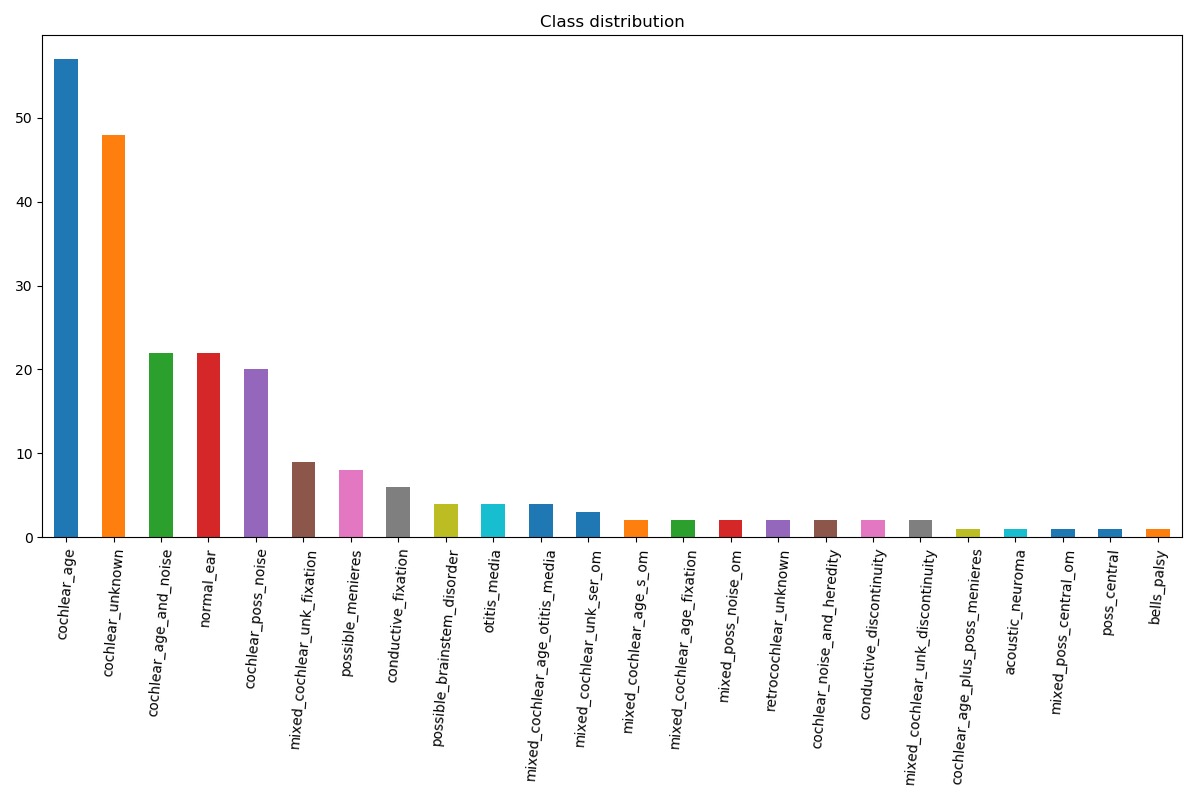
• Неравномерное распределение классов – с этим вы будете сталкиваться каждый день. Также разберемся, как с этим бороться.

Отдельное внимание хотелось бы уделить преобразованиям. Если мы проведем Label Encoding, размерность нашего входного вектора будет 69. Если проведем One Hot Encoding, размерность станет 161. Если проведем по-умному – 101.

Кто-то скажет, что нейронной сети будет достаточно провести Label Encoding – да, это так. Но в таком случае мы усложним ей обучение. Ну что же, поехали. Давайте прочитаем датасет и построим гистограмму распределений классов:

			df = pd.read_csv('Data/data.csv')

df['class'].value_counts().plot('bar', figsize=(12, 8))
plt.title('Class distribution')
plt.tight_layout()
plt.xticks(rotation=85)
plt.show()
		

Прежде всего надо посмотреть датасет. Видим, что большинство полей принимает значение t/f. Эти поля будут представлены как 1/0 соответственно. Вопрос, что делать с полями, у которых значения имеют вид mild, moderate, severe, normal, profound.

Хорошим решением будет One Hot Encoding. Выделим список колонок, которые требуют особой обработки, и проведем необходимые преобразования:

			encoding_columns = [
   'air()', 'ar_c()', 'ar_u()', 'bone()', 'bser()', 'o_ar_c()', 'o_ar_u()', 'speech()', 'tymp()'
]

//Таким образом мы проводим One Hot Encoding для перечисленных выше //колонок и немного расширяем наш DataFrame
df = pd.get_dummies(data=df, columns=encoding_columns)
		

Данные представлены в сыром виде, их нужно преобразовать в надлежащий. Вот так будет выглядеть кодировщик:

			from sklearn.preprocessing import LabelEncoder

class MultiColumnLabelEncoder:
   def __init__(self, columns=None):
       self.columns = columns

   def fit(self, X, y=None):
       return self

   def transform(self, X):
       output = X.copy()

       if self.columns is not None:
           output = output[self.columns]

           for col in self.columns:
               output[col] = LabelEncoder().fit_transform(output[col])
       else:
           for colname, col in output.iteritems():
               output[colname] = LabelEncoder().fit_transform(col)
       return output
		

При помощи класса выше мы преобразуем входные данные, а для выходных данных используем One Hot Encoding. Так, к примеру, класс с названием cochlear_unknown имеет следующий вид:

[ 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. ]

Теперь перейдем к сети. Какую структуру попробуем? Размерность входного вектора немаленькая, первый слой предлагаю взять 100 нейронов. Активация – сигмоид или тангенс, по усмотрению. Второй слой сделаем 150 нейронов. Выходной слой – 24. И давайте попробуем поставить активацию сигмоид на последний слой. Он как раз принимает значения от 0 до 1, т.е. подходит для нашей задачи.

Сниппет сети:

			import numpy as np
import cntk as C
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.metrics import accuracy_score
from data_processing import MultiColumnLabelEncoder

def create_model(input_):
   //Задаем случайное распределение весов и функцию активации по умолчанию - тангенс гиперболический
   with C.layers.default_options(activation=C.tanh, init=C.glorot_uniform()):
       model = C.layers.Sequential([
		//Первый скрытый слой
           C.layers.Dense(100),
		//Второй скрытый слой
           C.layers.Dense(150),
		//Выходной слой с активационной функцией - сигмоид
           C.layers.Dense(OUTPUT_DIM, activation=C.sigmoid)
       ])

   return model(input_)
		

Я взял тангенсы и сигмоид на последнем слое. Сконфигурируем гиперпараметры:

			TRAIN_SIZE = 200
INPUT_DIM = 101
OUTPUT_DIM = 24
LEARNING_RATE = 0.3
EPOCHS_COUNT = 1000
		

Подготовим и разобьем датасет:

			input_columns = list(df.columns)
input_columns.remove('indentifier')
input_columns.remove('class')

input_encoder = MultiColumnLabelEncoder(input_columns)

input_encoder.fit(df)
X = np.array(input_encoder.transform(df), dtype='float32')
Y = np.array(pd.get_dummies(df['class']), dtype='float32')

train_X = X[:TRAIN_SIZE]
train_Y = Y[:TRAIN_SIZE]
test_X = X[TRAIN_SIZE:]
test_Y = Y[TRAIN_SIZE:]

//Подготовим плейсхолдеры, которые “свяжут мир с сетью” и “сеть с //миром”
input_ = C.input_variable(INPUT_DIM, 'float32')
output_ = C.input_variable(OUTPUT_DIM, 'float32')
		

Конфигурируем обучение:

			z = create_model(input_)

lr_schedule = C.learning_rate_schedule(LEARNING_RATE, C.UnitType.minibatch)

learner = C.adam(z.parameters, lr_schedule, momentum=0.9)

//Относительно чего мы оптимизируем нашу сеть
loss = C.squared_error(z, output_)
//Функция которая отображает вероятность неправильной классификации
error = C.classification_error(z, output_)

trainer = C.Trainer(z, (loss, error), [learner])
		

В качестве оптимизатора был взят «адам», как и в прошлый раз, ускорение – 0.9. Но теперь есть одно нововведение. Вторым параметром в Trainer передается пара – loss и error. Оптимизация проходит относительно функции потерь (квадратическая ошибка), error – функция оценки ошибки классификации, ее значение показывает, сколько процентов от учебных данных классифицируется ошибочно на данный момент. Довольно удобная вещь, позволяет наглядно смотреть за процессом обучения при задаче классификации.

Проводим обучение и отображаем значения функции ошибки:

			datamap = {
  input_: train_X,
  output_: train_Y
}

error_function = []

for i in range(EPOCHS_COUNT):
   trainer.train_minibatch(datamap)
   error_function.append(trainer.previous_minibatch_evaluation_average)


plt.plot(error_function)
plt.title('Error function')
plt.ylabel('Error')
plt.xlabel('Epochs')
plt.show()
		

Ошибка нулевая, научились всему (а опытные даже скажут, что произошло переобучение (overfitting), но об этом позже). Посмотрим на точность модели на тестовых данных:

			y_pred = np.argmax(z(test_X), axis=1)
y_true = np.argmax(test_Y, axis=1)

print('Accuracy: {val}'.format(val=accuracy_score(y_true, y_pred)))
		

76.9%. Неплохо, учитывая распределение классов, но и не фонтан. Итак, настало время знакомства с перекрестной энтропией. Это несколько иной критерий оптимизации, в двух словах он уменьшает меру неопределенности нашего классификатора. В нейронных сетях он обычно работает в связке с функцией SoftMax.

Для того чтобы вы не терялись, давайте разберем обе функции. Начнем с простого – SoftMax.

Далеко ходить не будем, возьмем определение с Википедии.

Softmax — это обобщение логистической функции для многомерного случая. Функция преобразует вектор z размерности K в вектор  той же размерности, где каждая координата полученного вектора представлена вещественным числом в интервале [0,1] и сумма координат равна 1.

Главное преимущество функции в том, что получив на вход, условно говоря, непонятные значения, функция выдаст вероятности, причем так, что их сумма будет равна 1. Иными словами, это очень хороший выбор, когда объект может быть носителем одного класса.
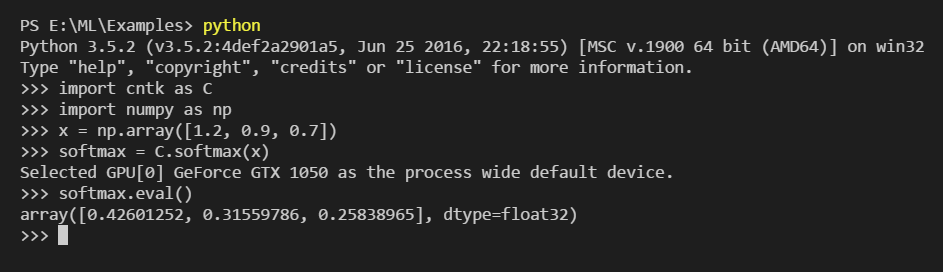
Для наглядности запустим тот же CNTK и посмотрим, как работает эта функция вживую. Введем какие-то случайные значения для массива x. Условно назовем их попугаями, а потом применим к ним SoftMax:

Так и вышло. На входе получили попугаи, на выходе – «причесанные» вероятности.

Теперь сложная часть — энтропия. Формул довольно много и многим они ничего не скажут, поэтому для того чтобы у вас было хотя бы интуитивное понимание, что это такое, начнем с энтропии. Энтропия – это мера неопределенности случайной величины.

Оптимизируя (минимизируя, если быть точным) энтропию случайной величины, которая порождается ответами нашей нейронной сети, мы минимизируем неопределенность (непредсказуемость) классификации объекта. Для приличия все же оставлю формулу:

И пока эта математика не вылетела у вас из головы, меняем конфигурацию сети следующим образом:

			def create_model(input_):
   with C.layers.default_options(activation=C.tanh, init=C.glorot_uniform()):
       model = C.layers.Sequential([
           C.layers.Dense(100),
           C.layers.Dense(150),
           C.layers.Dense(OUTPUT_DIM, activation=None)
       ])

   model = C.softmax(model)
   return model(input_)
		

Активацию из последнего слоя убрали и заменили ее функцией SoftMax.

Меняем критерий оптимизации – квадратическую ошибку заменяем перекрестной энтропией:

			z = create_model(input_)

lr_schedule = C.learning_rate_schedule(LEARNING_RATE, C.UnitType.minibatch)

learner = C.adam(z.parameters, lr_schedule, momentum=0.9)

loss = C.cross_entropy_with_softmax(z, output_)
error = C.classification_error(z, output_)

trainer = C.Trainer(z, (loss, error), [learner])
		

Запускаем обучение и смотрим точность: 84.61 процента. Это уже на порядок лучше, нежели 76.9%. Мораль следующая: критерии оптимизации необходимо подбирать в соответствии с поставленной задачей. Если перед вами стоит задача классификации, задумайтесь над применением оптимизации перекрестной энтропии, возможно SoftMax. В случае, когда классов уже 3 и более или они неравномерно распределены, перекрестная энтропия справляется лучше, чем квадратическое отклонение.

Продолжение следует…

Авторы:
Александр Ганджа, CTO DataTrading
Богдан Домненко, Data Scientist DataTrading